варианты!
1.Бобнихов
2.волынский
3.Гизатулин
4.кабанов
5.-
6.Корнейчук
7.Кулинич
8.Лактионов
9.Лопатинская
10.матвеева
11.Савинов
12.Самойленко
13.-
14.Спицина
15.Страшко
16.Тертычный
17.Федоров
18.Честа
Министерство образования и науки Украины
ДВНЗ «Донецкий национальный технический университет»
Кафедра автоматики и телекоммуникаций
Методические указания к выполнению лабораторных работ
по курсу: "Основы дискретной математики"
для студентов специальностей 091401, 092401
«Системы управления и автоматика»,
«Телекоммуникационные системы и сети»
Рассмотрен на заседании кафедры автоматики и телекоммуникаций.
Протокол № 11
от « 22 » октября 2010 р.
Утвержден на заседании научно-издательского совета ДонНТУ
Протокол № ___
от «___»___________2010 р.
Донецк, ДонНТУ 2010
УДК 681.3.07
Методические указания к лабораторным работам по курсу "Основы дискретной математики" для студентов специальностей 091401, 092401 «Системы управления и автоматика», «Телекоммуникационные системы и сети» / доц. Жукова Н.В., ас. Зайцева Э.Е. – Донецк, ДонНТУ. 2010. – 45 с.
Методические указания содержат лабораторные работы по основным разделам курса ОДМ и предназначены для студентов специальностей 091401, 092401 «Системы управления и автоматика», «Телекоммуникационные системы и сети».
Составитель доц. Жукова Н.В., ас. Зайцева Э.Е.
Рецензент доц. Ф-ту КНТ каф. АСУ Светличная В.А.
доц. Ф-ту КИТА каф. ЭТ Тарасюк В.П.
Ответственный за выпуск доц. Бессараб В.И.
Содержание
1. Лабораторная работа №1.
Множества, операции над множествами…………………...............……………4
2. Лабораторная работа №2.
Алгебра высказываний……………………………….................….…...................9
3. Лабораторная работа №3.
Минимизация булевых функций. Логические схемы……..……………………17
4. Лабораторная работа №4.
Конечные автоматы с памятью..…………………………………………………32
СПИСОК ЛИТЕРАТУРЫ…………………………………………………………45
Лабораторная работа № 1
Тема: «Множества, основные операции над множествами»
Цель: Приобретение практических навыков работы с множествами
Теоретические сведения [1].
Операции над множествами
Опишем основные способы получения новых множеств из уже имеющихся. Эти способы называются операциями над множествами.
Объединение множеств
Объединением
множеств
и
называется множество, которое обозначается
(иногда
)
и состоящее из всех тех и только тех
элементов, которые принадлежат множеству
или множеству
.
Приведем графическую иллюстрацию операции объединения двух множеств:
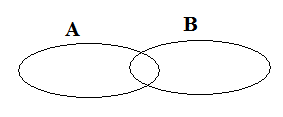
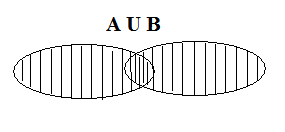
Выражение
читается: «объединение множества
и множества
».
Часто операцию объединения двух множеств
записывают в виде:
,
который
возможно использовать, учитывая, что
множество элементов
– это множество «всех тех и только тех
элементов, которые принадлежат множеству
или множеству
».
Пересечение множеств
Пересечением
множеств
и
называется множество, которое обозначается
(иногда
)
и состоящее из всех тех и только тех
элементов, которые принадлежат каждому
из множеств
и
.
Приведем графическую иллюстрацию операции пересечения двух множеств:
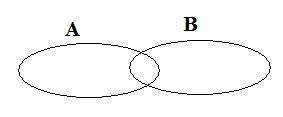
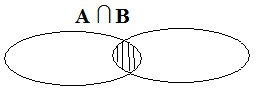
Выражение
читается: «пересечение множества
и множества
».
Часто операцию пересечения двух множеств записывают в виде:
,
который
возможно использовать, учитывая, что
множество элементов
– это множество «всех тех и только тех
элементов, которые принадлежат каждому
из множеств
и
».
Разность множеств
Рассмотрим операцию над множествами, которая определяется только для двух множеств.
Разностью
множеств
и
называется множество, которое обозначается
(иногда
)
и состоящее из всех тех и только тех
элементов множества
,
которые не является элементами множества
.
Приведем графическую иллюстрацию операции разности двух множеств:
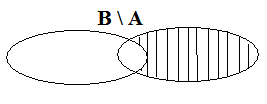
Выражение
читается: «разность множества
и множества
».
Часто
операцию разности двух множеств
и
записывают в виде:
,
который
возможно использовать, учитывая, что
множество элементов
– это множество «всех тех и только тех
элементов множества
,
которые не являются элементами множества
».
Универсальное множество и дополнение множества
Как правило, при определении конкретного множества явно или неявно (интуитивно) ограничивается собрание допустимых объектов. Например, говоря о слонах, говорят о млекопитающих; говоря о натуральных числах, предполагают задание множества целых или действительных чисел.
Удобно
совокупность допустимых объектов
зафиксировать и считать, что рассматриваемые
множества состоят из элементов этой
совокупности. Искомую совокупность
называют универсальным множеством или
универсумом и обозначают
.
В соответствии с этим любое множество будем рассматривать в связи с универсумом, который при графической иллюстрации будем изображать прямоугольником, а множества будем изображать внутри данного прямоугольника.
В
соответствии с введением множества
разность
будем называть дополнением множества
(до множества
)
и обозначать
.
Симметрическая разность
Симметрической
разностью множеств
и
называется множество, которое обозначается
(иногда
)
и определенное следующим образом:
.
Приведем графическую иллюстрацию операции симметрической разности двух множеств:
Пример. Записать с помощью операций над множествами выражение для множества, соответствующего заштрихованной области диаграммы:
►
или
.
◄
П
ример.
С помощью графической интерпретации
изобразить множество
,
если
образовано множествами
,
и
:
.
► Изобразим
множества
,
и
на диаграмме Эйлера-Венна, как показано
на рисунке ниже.
М
ножество
есть объединение трех множеств,
,
и
.
Рассмотрим множество
.
Его элементами являются элементы
множества
,
которые не принадлежат
и не принадлежат
.
Аналогично, множество
состоит из элементов
,
не принадлежащих
или
.
Элементы множества
– есть элементы
,
не принадлежащие ни
,
ни
,
ни
.
Таким образом, множество
на диаграмме Эйлера-Венна имеет вид
(заштрихованным областям соответствует
серый цвет):
◄
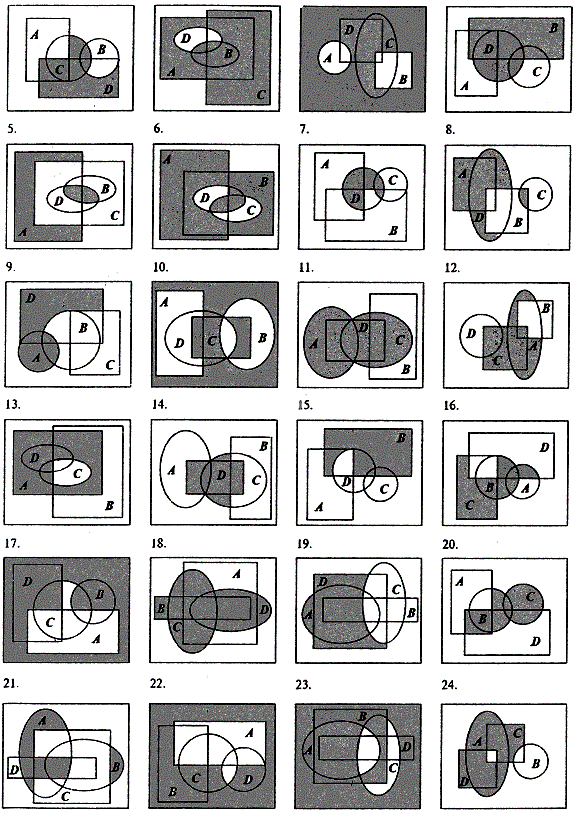
Задание.
Ниже приведены диаграммы Виенна. Представьте заштрихованную и отдельно незаштрихованную области максимально компактными аналитическими выражениями, в которых бы использовались минимальное количество логических операций и букв. Результаты проверьте по таблицам истинности.
1.3. Контрольные вопросы
1.3.1. Дайте определение конечного множества, элементов множества.
1.3.2. Какие существуют основные способы задания множества?
1.3.3. Какие множества называются равными? Что такое подмножество?
1.3.4. Назовите основные операции над множествами, какой наглядный инструмент используется для иллюстрации операций над множествами?
1.3.5.
Докажите свойство если
и
,
то
.
1.3.6.
Перечислите свойства операций над
множествами, докажите
,
.
1.3.7. Дайте определение прямому (декартовому) произведению множеств;
1.3.8. Записать с помощью операций над множествами выражение для множества, соответствующего закрашенной области диаграммы:
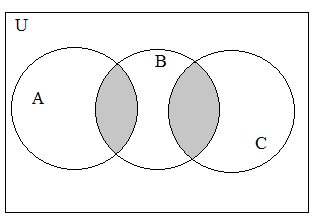
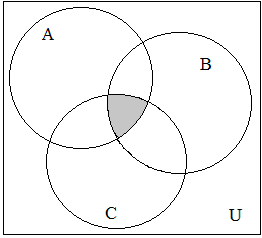
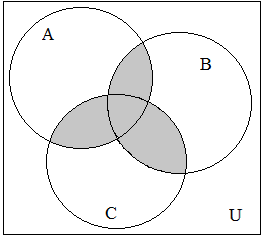
1.3.9.
С помощью графической интерпретации
изобразить множество
,
если
образовано множествами
,
,
и
:
;
;
;
;
;
.
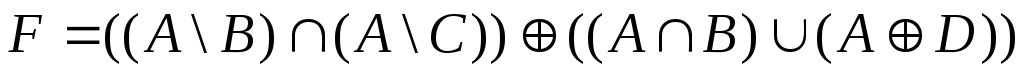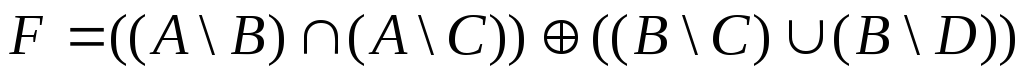1.3.10. Доказать тождества
;
;
;
;
;
;
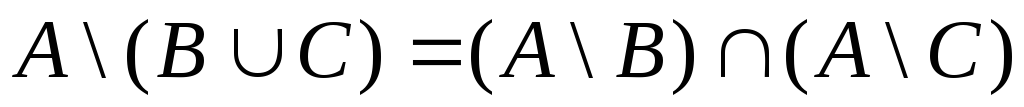
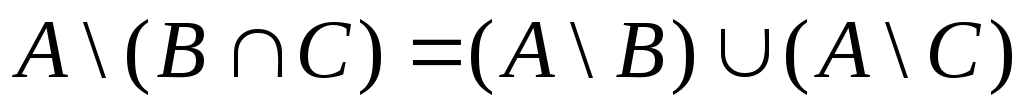
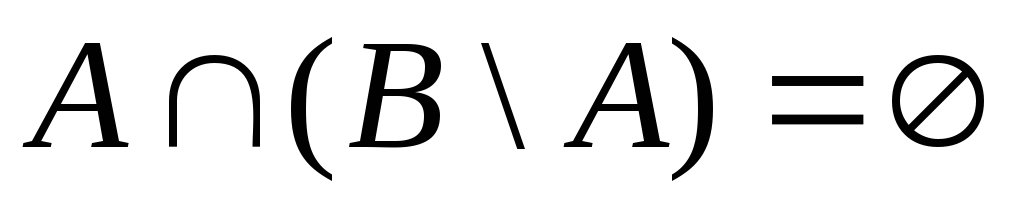