19.5. Понятие о математической лингвистике

Язык – важнейшее средство человеческого общения – социальное средство хранения и передачи информации, одно из средств управления человеческим поведением.

До начала XX в., говоря о языках, имели в виду только естественные языки (русский, английский и т.д.). В конце прошлого века была предпринята попытка создать искусственный язык – Эсперанто.

Лингвистика – наука о языках – сводилась в основном к изучению конкретных естественных языков, их классификации, выяснению сходств и различий между ними. Возникновение математики, логико-философского исследования языка науки, привели к появлению идеи структуралистского подхода к лингвистике [19].

Язык может быть описан математическими средствами, как преобразование некоторых абстрактных объектов – смыслов, в некоторые объекты – тексты и обратно [29].

Преобразование объектов языка выглядит следующим образом:

1) переход от смыслов к синтаксическим структурам без линейного порядка;

2) переход к линейным последовательностям слов;

3) получение цепочек звуков.

Язык – частный случай знаковой системы.

Наиболее хорошо исследованы знаковые системы, в которых знаками являются символы алфавитов, а последовательностями знаков – тексты; к таким знаковым системам относятся естественные языки, языки науки, а так же сильно развившиеся за последние 60 лет языки программирования.

Математическая лингвистика – математическая дисциплина, предметом которой является разработка формального аппарата для описания строения естественных и некоторых искусственных языков.

Математическая лингвистика является ответвлением математической логики.

Наибольших успехов математическая лингвистика достигла в изучении синтаксиса, где за последние годы сложился специальный математический аппарат – теория формальных языков и грамматик.

19.6. Формальный язык

Формальный язык в отличие от естественного, допускающего неоднозначность, двусмысленность, строится по математически строгим и точным правилам. Он применяется для описания искусственных языков, например, языков программирования.

Задается алфавит V={a,b,c,….x,y,z}, состоящий из букв или символов [4]. Иногда буквы нумеруют, как в алфавите русского языка «а» – первая буква, «я» – последняя. Тогда V^k – множество слов из k букв.

Цепочки.

Слово ωV^k называется еще цепочкой ω. Длина цепочки обозначается |ω|.

При k=0 получаем пустое слово, обозначаемое . ||=0.

V^* – множество всех слов – эквивалент универсума в теории множеств.

Нетрудно видеть, что V^* счетно. Пусть V={а,b}. Будем нумеровать слова [4]: а=1, b=2, аа=3=(12¹+12⁰), аb=4=(12¹+22⁰), bа=5=(22¹+12⁰), bb=6=(22¹+22⁰) и т.д. Получилась так называемая лексико-графическая нумерация. Таким образом, по каждой цепочке можно получить ее номер. У пустой цепочки номер 0. По номеру можно получить цепочку в заданном алфавите.

Пусть V={а,b,с}. Получим цепочку №20. Предварительно введем таблицу формирования номера в таком алфавите (табл. 89).

Таблица 89

Формирование номера цепочки в V={а,в,с}

27	9	3	1	а
162	18	6	2	b
243	27	9	3	с

Тогда 20=9+9+2, то есть (13²+33¹+23⁰), получаем цепочку асb.

Подобным образом можно нумеровать и другие объекты. Получим, например, номер формулы логики высказываний АВ. Алфавит: {А,В,,¯}, тогда номер цепочки: (13² +33¹+23⁰)=20.

В этой цепочке старший (левый) разряд А, номер символа А в алфавите равен 1, вес его =3²; следующий символ , номер символа  равен 2, вес его =3¹; младший (правый) символ В, номер символа В равен 3, вес =3⁰. Ясно, что не все номера представляют собой правильные формулы. Например, формула АВ – неправильная. Хотя в случае использования так называемой префиксной формы записи (символ бинарной операции ставится перед символами переменных – это польская инверсная запись ПОЛИЗ) эта формула будет правильной.

Получим номер автомата – распознавателя последовательности 0132 в алфавите {0,1,2,3}:

(13³+23²+43¹ +33⁰)=60.

Получим номер алгоритма по его логической схеме: в алфавите {}:=16186.

Получим номер модуса Barbara в виде ааа1 (1 – номер фигуры) в алфавите {a,i,e,o,1,2,3,4}, где буква – вид суждения, цифра – номер модуса:

(18³+18²+18¹ +58⁰)=589.

Над цепочками вводятся операции, например:

• конкатенации  (сцепления), например, аbbc=аbbс;

• итерации * (повторения), например: а(bbа)*=аbbаbbаbbа…;

• инверсии (реверса), например,;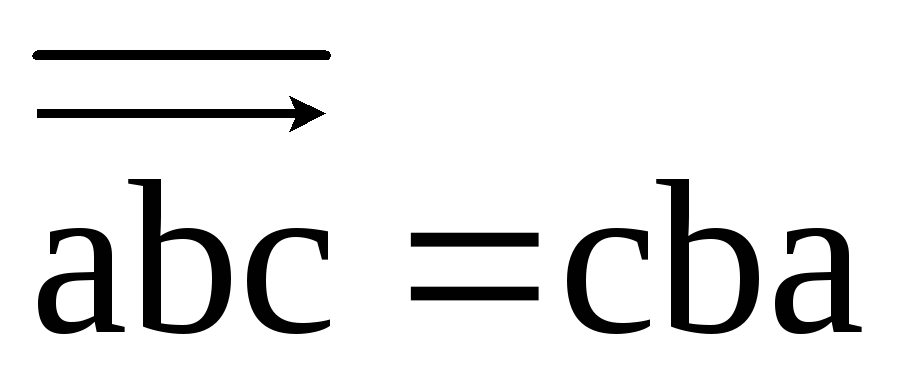

• циклического сдвига  (циклической перестановки символов), например, влево: (аbс)=bса, или вправо: (аbс)=саb;

• перестановки групп символов (подцепочек данной цепочки), например, (ав(вс)(ав))=ававвс;

• замены одной подцепочки данной цепочки другой цепочкой: (аbbс,bbd)=adc.

Ранее мы упоминали о генетических алгоритмах. В них цепочками представляются некоторые варианты решения комбинаторной задачи. Такие цепочки называют как в генетике – хромосомами. В процессе «скрещивания» двух хромосом образуется новая хромосома, то есть цепочка, состоящая из частей «родительских» цепочек. В дальнейшем в процессе «эволюции» остаются или «выживают» только самые жизнеспособные, т.е. лучшие варианты. Так происходит и в природе. Все мы носим эти цепочки хромосом с собой и, возможно, передадим их частички в будущее. Не будем забывать заветы великого Дарвина: «Выживает сильнейший», в смысле – умнейший. Хотя, точнее, – тот, кто приспосабливается к изменениям.

Операции над языками.

Формальный язык L в алфавите V – это некоторое подмножество: V^* LV^*.

Над языками, как над множествами вводятся теоретико-множественные операции: объединение, пересечение, разность. На декартово произведение похоже соединение (конкатенация) языков, например: L₁={па,ма,да}, L₂={па,к}, тогда L₁L₂={папа,пак,мапа,мак,дапа,дак}.

Очевидно, что L₂²={па,к}{па,к}={папа,пак,кпа,кк}.

Имеется также операция подстановки языка в язык [19]. Пусть заданы языки сумм:

L_cm={а,а+а,а+а+а,…} и произведений L_np={а,аа,ааа,…}. Подстановка L_cm(аL_np) дает язык сумм произведений L_cn={аа,ааа,…аа+а,…}.

Итерация языка – это объединение всех его степеней:

Определение языков – это их задание. Оно осуществляется следующими способами:

• перечислением всех правильных цепочек языка;

• порождением всевозможных цепочек и их «фильтрацией» с помощью так называемых распознавателей, которые распознают требуемые цепочки;

• заданием соответствующей формальной грамматики, определяющей правила построения языка.

Рассмотрим формальные грамматики.