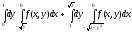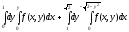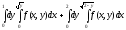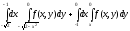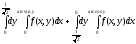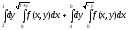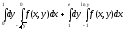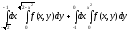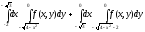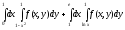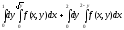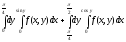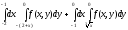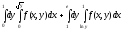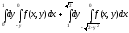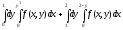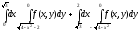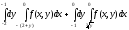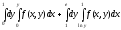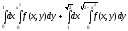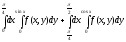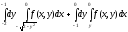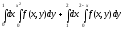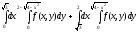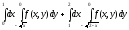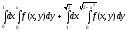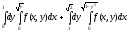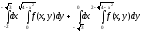Инд.зад.13, 14 кратн.и кривол.интегралы
.docxТема 13. КРАТНЫЕ ИНТЕГРАЛЫ
Задание 1. Написать уравнения линий, ограничивающих область интегрирования, и изменить порядок интегрирования.
-
Задание 2. Вычислить двойной интеграл по области s, ограниченной заданными линиями.
-
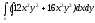
-
s: x=1, y=x2,
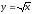
-
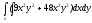
-
s: x=1, y= - x2,
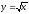
-
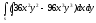
-
s: x=1, y= - x3,
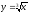
-
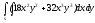
-
s: x=1, y= x3,
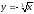
-
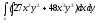
-
s: x=1, y= x2,

-
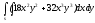
-
s: x=1, y= - x2,
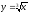
-
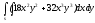
-
s: x=1, y= x3,
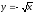
-
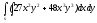
-
s: x=1, y= - x3,
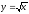
-

-
s: x=1, y= x2,
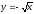
-
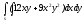
-
s: x=1, y= - x2,
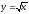
-
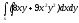
-
s: x=1, y= - x3,
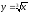
-
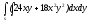
-
s: x=1, y= x3,
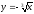
-
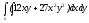
-
s: x=1, y= x2,
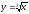
-
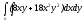
-
s: x=1, y= - x2,
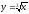
-
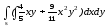
-
s: x=1, y= x3,
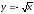
-
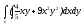
-
s: x=1, y= - x3,
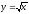
-
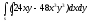
-
s: x=1, y= x2,

-
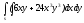
-
s: x=1, y= - x2,
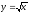
-

-
s: x=1, y= - x3,

-

-
s: x=1, y= x3,
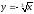
-
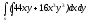
-
s: x=1, y= x2,
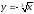
-

-
s: x=1, y= - x2,
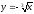
-
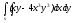
-
s: x=1, y= x3,
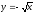
-
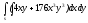
-
s: x=1, y= - x3,
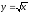
-
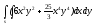
-
s: x=1, y= x2,
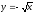
-

-
s: x=1, y= - x2,
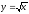
-
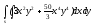
-
s: x=1, y= - x3,
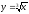
-
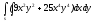
-
s: x=1, y= x3,
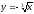
-
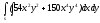
-
s: x=1, y= x2,
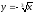
-
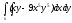
-
s: x=1, y=- x2,
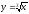
-
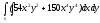
-
s: x=1, y= x3,
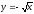
-

-
s: x=1, y= x2,
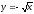
-
Задание 3. Вычислить двойной интеграл по заданной области.
-
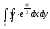
-
s: у=ln2, y= ln3, x=2, x=4
-
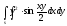
-
s: у=
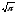 ,
,
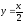 ,
x=0
,
x=0 -

-
s: у=
 ,
,
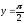 ,
x=1, x=2
,
x=1, x=2 -

-
s: у=2, y= x, x=0
-
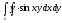
-
s: у=
 ,
,
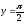 ,
x=1, x=2
,
x=1, x=2 -
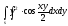
-
s: у=
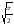 ,
,
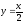 ,
x=0
,
x=0 -
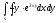
-
s: у=ln3, y= ln4,
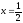 ,
x=1
,
x=1 -
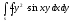
-
s: у=x,
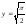 ,
x=0
,
x=0 -
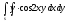
-
s: у=
 ,
,
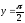 ,
,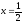 , x=1
, x=1 -
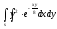
-
s: у=2,
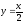 ,
x=0
,
x=0 -
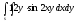
-
s:
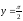 ,
,
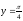 ,
x=2, x=3
,
x=2, x=3 -
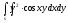
-
s: у=x,
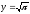 ,
x=0
,
x=0 -
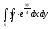
-
s: у=ln2, y=ln3, x=4, x=8
-
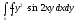
-
s: у=2x,
 ,
x=0
,
x=0 -

-
s:
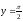 ,
,
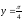 ,
x=1, x=2
,
x=1, x=2 -
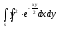
-
s: у=x,
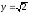 ,
x=0
,
x=0 -
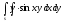
-
s:
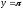 ,
,
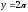 ,
,
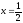 ,
x=1
,
x=1 -

-
s:
 ,
,
 ,
x=0
,
x=0 -
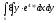
-
s: у=ln3, y= ln4,
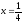 ,
,
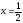
-
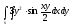
-
s: у=
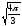 ,
,
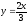 ,
x=0
,
x=0 -
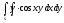
-
s:
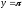 ,
,
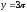 ,
x=1,
,
x=1,

-
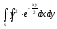
-
s: у=1,
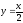 ,
х=0
,
х=0 -
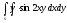
-
s:
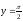 ,
,
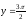 ,
,
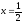 ,
x=2
,
x=2 -
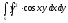
-
s: у=
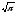 ,
,
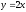 ,
x=0
,
x=0 -
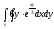
-
s: у=ln2, y= ln3,
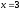 ,
,

-
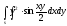
-
s: у=
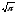 ,
,
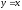 ,
x=0
,
x=0 -
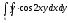
-
s:
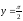 ,
,
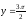 ,
,
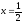 ,
x=2
,
x=2 -
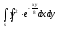
-
s: у=4, y=2x,

-
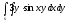
-
s:
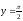 ,
,
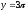 ,
,
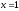 ,
x=3
,
x=3 -
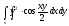
-
s:
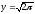 ,
,
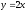 ,
,
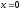
-
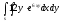
-
s: у=ln2, y= ln4,
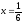 ,
,
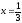
-
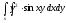
-
s:
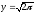 ,
,
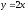 ,
,
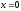
-
Задание 4. С помощью двойного интеграла найти площадь фигуры, ограниченной данными линиями.
-
 ,
у = 4ех, у = 3, у = 4.
,
у = 4ех, у = 3, у = 4. -
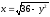 ,
,
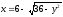 .
. -
х2 + у2 = 72, 6у = - х2, (
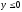 ).
). -
х = 8 – у2, х = 2у.
-
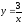 ,
у = 8ех, у = 3, у = 8.
,
у = 8ех, у = 3, у = 8. -
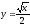 ,
,
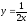 ,
х = 16.
,
х = 16. -
х = 5 – у2, х = -4у.
-
х2 + у2 = 12,
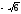 у
= - х2, (
у
= - х2, ( ).
). -
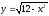 ,
,
 ,
х = 0, (
,
х = 0, (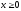 ).
). -
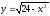 ,
,
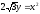 ,
х = 0, (
,
х = 0, (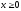 ).
). -
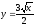 ,
,
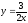 ,
х = 9.
,
х = 9. -
у = sin x, y = cos x, x = 0, (
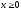 ).
). -
y = 20 – x2, y = - 8x.
-
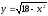 ,
,
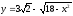 .
. -
y = 32 – x2, y = - 4x.
-
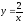 ,
у = 5ех,
у = 2, у = 5.
,
у = 5ех,
у = 2, у = 5. -
х2 + у2 = 36,
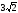 у
= х2, (
у
= х2, ( ).
). -
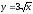 ,
,
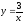 ,
х = 4.
,
х = 4. -
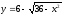 ,
,
 ,
x = 0, (
,
x = 0, (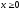 )
) -
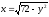 ,
,
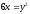 ,
y = 0, (
,
y = 0, ( )
) -
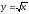 ,
,
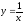 ,
х = 16.
,
х = 16. -
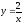 ,
у = 7ех,
у = 2, у = 7.
,
у = 7ех,
у = 2, у = 7. -
x = 27 – y2, x = - 6y.
-
y =
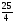 – x2,
– x2,
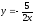 .
. -
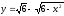 ,
,
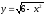 .
. -
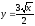 ,
,
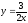 ,
х = 4.
,
х = 4. -
у = sin x, y = cos x, x = 0, (
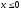 ).
). -
 ,
у = 6ех, у = 1, у = 6.
,
у = 6ех, у = 1, у = 6. -
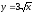 ,
,
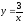 ,
х = 9.
,
х = 9. -
y = 11 – x2, y = - 10x.
-
х2 + у2 = 12,
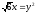 ,
(
,
(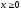 ).
). -
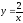 ,
у = 3ех, у = 1, у = 3.
,
у = 3ех, у = 1, у = 3.
-
Задание 5. При помощи двойного интеграла вычислить объем тела, ограниченного данными поверхностями.
-
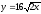 ,
,
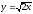 ,
z = 0, x
+ z = 2.
,
z = 0, x
+ z = 2. -
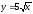 ,
,
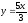 ,
z = 0,
,
z = 0,
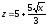 .
. -
x2 + y2 = 2,
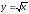 ,
,
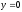 ,
z = 0,
,
z = 0,
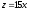 .
. -
x – y = 2,
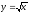 ,
z = 12y,
z = 0.
,
z = 12y,
z = 0. -
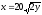 ,
,
 ,
z = 0, y
+ z =
,
z = 0, y
+ z =
 .
. -
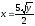 ,
,
 ,
z = 0,
,
z = 0,
 .
. -
x2 + y2 = 2,
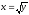 ,
,
 ,
z = 0,
,
z = 0,
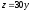 .
. -
x + y = 2,
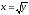 ,
,
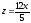 ,
z = 0.
,
z = 0. -
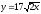 ,
,
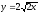 ,
z = 0, x
+ z =
,
z = 0, x
+ z =
 .
. -
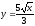 ,
,
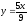 ,
z = 0,
,
z = 0,
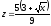 .
. -
x2 + y2 = 8,
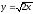 ,
,
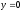 ,
z = 0,
,
z = 0,
 .
. -
x – y = 4,
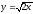 ,
z = 3y,
z = 0.
,
z = 3y,
z = 0. -
 ,
,
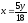 ,
z = 0,
,
z = 0,
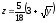 .
. -
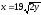 ,
,
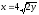 ,
z = 0, y
+ z =2.
,
z = 0, y
+ z =2. -
x2 + y2 = 8,
 ,
,
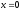 ,
z = 0,
,
z = 0,
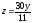 .
. -
x + y = 4,
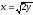 ,
,
 ,
z = 0.
,
z = 0. -
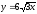 ,
,
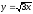 ,
z = 0, x
+ z =3.
,
z = 0, x
+ z =3. -
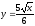 ,
,
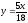 ,
z = 0,
,
z = 0,
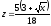 .
. -
x2 + y2 = 18,
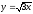 ,
,
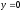 ,
z = 0,
,
z = 0,
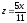 .
. -
x – y = 6,
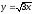 ,
z = 4y,
z = 0.
,
z = 4y,
z = 0. -
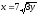 ,
,
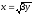 ,
z = 0, y
+ z =3.
,
z = 0, y
+ z =3. -
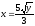 ,
,
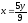 ,
z = 0,
,
z = 0,
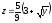 .
. -
x2 + y2 = 18,
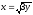 ,
,
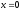 ,
z = 0,
,
z = 0,
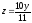 .
. -
x + y = 6,
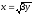 ,
,
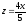 ,
z = 0.
,
z = 0. -
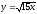 ,
,
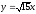 ,
z = 0,
,
z = 0,
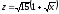 .
. -
x2 + y2 = 50,
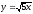 ,
,
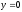 ,
z = 0,
,
z = 0,
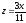 .
. -
x – y = 8,
 ,
z = 3y,
z = 0.
,
z = 3y,
z = 0. -
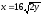 ,
,
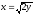 ,
z = 0, y
+ z =2.
,
z = 0, y
+ z =2. -
 ,
,
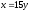 ,
z = 0,
,
z = 0,
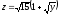 .
. -
x2 + y2 = 50,
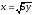 ,
,
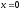 ,
z = 0,
,
z = 0,
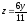 .
. -
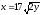 ,
,
 ,
z = 0, y
+ z =
,
z = 0, y
+ z = .
. -
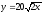 ,
,
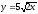 ,
z = 0, y
+ z =
,
z = 0, y
+ z = .
.
-
Задание 6. Вычислить двойной интеграл, переходя к полярным координатам.
-

-
s:
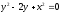 ,
,
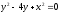 ,
, -
 ,
,
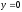 ,
,
 .
. -
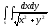
-
s:
 ,
,
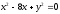 ,
, -
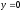 ,
,
 .
. -
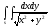
-
s:
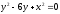 ,
,
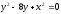 ,
, -
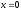 ,
,
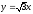 .
. -
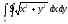
-
s:
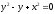 ,
,
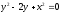 ,
, -
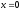 ,
,
 ,
,
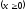 .
. -
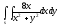
-
s:
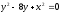 ,
,
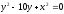 ,
, -
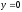 ,
,
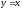 .
. -
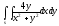
-
s:
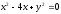 ,
,
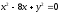 ,
, -
 ,
,
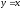 .
. -
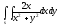
-
s:
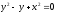 ,
,
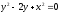 ,
, -
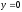 ,
,
 ,
,
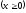 .
. -
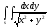
-
s:
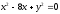 ,
,
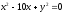 ,
, -
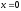 ,
,
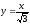 .
. -

-
s:
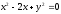 ,
,
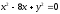 ,
, -
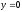 ,
,
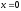 ,
,
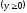 .
. -
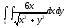
-
s:
 ,
,
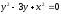 ,
, -
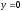 ,
,
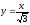 .
. -
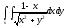
-
s:
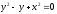 ,
,
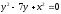 ,
, -
 ,
,
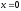 ,
,
 .
. -
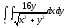
-
s:
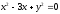 ,
,
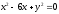 ,
, -
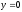 ,
,
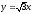 .
. -
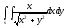
-
s:
 ,
,
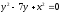 ,
, -
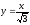 ,
,
 .
. -
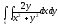
-
s:
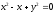 ,
,
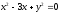 ,
, -
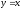 ,
,
 .
. -
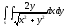
-
s:
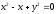 ,
,
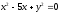 ,
, -
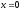 ,
,
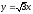 .
. -

-
s:
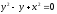 ,
,
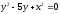 ,
, -
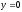 ,
,
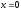 ,
,
 .
. -
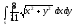
-
s:
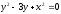 ,
,
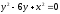 ,
, -
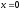 ,
,
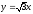 .
. -
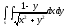
-
s:
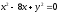 ,
,
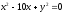 ,
, -
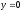 ,
,
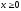 ,
,
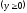 .
. -
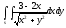
-
s:
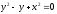 ,
,
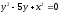 ,
, -
 ,
,
 ,
,
 .
. -
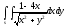
-
s:
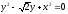 ,
,
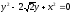 ,
, -
 ,
,
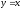 .
. -
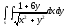
-
s:
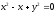 ,
,
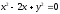 ,
, -
 ,
,
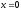 ,
,
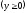 .
. -
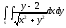
-
s:
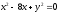 ,
,
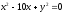 ,
, -
 ,
,
 ,
,
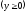 .
. -
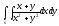
-
s:
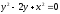 ,
,
 ,
, -
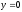 ,
,
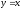 .
. -
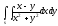
-
s:
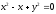 ,
,
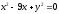 ,,
,, -
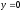 ,
,
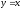 .
. -
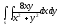
-
s:
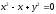 ,
,
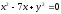 ,,
,, -
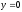 ,
,
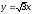 .
. -
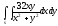
-
s:
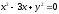 ,
,
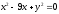 ,,
,, -
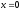 ,
,
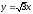 .
. -
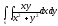
-
s:
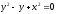 ,
,
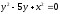 ,
, -
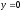 ,
,
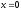 ,
,
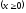 .
. -
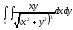
-
s:
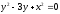 ,
,
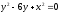 ,
, -
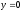 ,
,
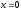 ,
,
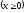 .
. -
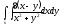
-
s:
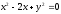 ,
,
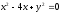 ,,
,, -
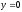 ,
,
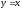 .
. -
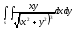
-
s:
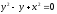 ,
,
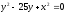 ,
, -
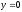 ,
,
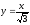 .
. -

-
s:
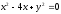 ,
,
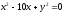 ,
, -
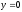 ,
,
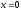 ,
,
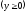 .
. -
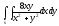
-
s:
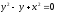 ,
,
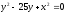 ,
, -
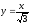 ,
,
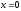 .
.
-
Задание 7. Пластинка s задана ограничивающими ее кривыми,
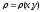 - поверхностная плотность. Найти массу
пластинки.
- поверхностная плотность. Найти массу
пластинки.
-
s: х2 + у2 = 1, х2 + у2 = 25, х = 0, у = 0, (
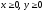 ),
),
 .
. -
s: х2 + у2 = 1, х2 + у2 = 4, х = 0, у = 0, (
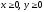 ),
),
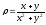 .
. -
s: х2 + у2 = 16, х2 + у2 = 25, х = 0, у = 0, (
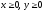 ),
),
 .
. -
s: х2 + у2 = 9, х2 + у2 = 16, х = 0, у = 0, (
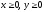 ),
),
 .
. -
s: х2 + у2 = 4, х2 + у2 = 16, х = 0, у = 0, (
 ),
),
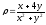 .
. -
s: х2 + у2 = 1, х2 + у2 = 16, х = 0, у = 0, (
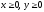 ),
),
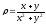 .
. -
s: х2 + у2 = 1, х2 + у2 = 9, х = 0, у = 0, (
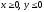 ),
),
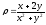 .
. -
s: х2 + у2 = 4, х2 + у2 = 25, х = 0, у = 0, (
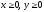 ),
),
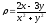 .
. -
s: х2 + у2 = 4, х2 + у2 = 9, х = 0, у = 0, (
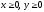 ),
),
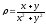 .
. -
s: х2 + у2 = 1, х2 + у2 = 9, х = 0, у = 0, (
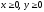 ),
),
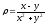 .
. -
s: х2 + у2 = 9, х2 + у2 = 25, х = 0, у = 0, (
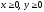 ),
),
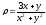 .
. -
s: х2 + у2 = 9, х2 + у2 = 25, х = 0, у = 0, (
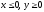 ),
),
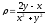 .
. -
s: х2 + у2 = 16, х2 + у2 = 25, х = 0, у = 0, (
 ),
),
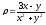 .
. -
s: х2 + у2 = 4, х2 + у2 = 16, х = 0, у = 0, (
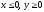 ),
),
 .
. -
s: х2 + у2 = 9, х2 + у2 = 16, х = 0, у = 0, (
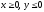 ),
),
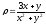 .
. -
s: х2 + у2 = 9, х2 + у2 = 16, х = 0, у = 0, (
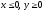 ),
),
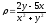 .
. -
s: х2 + у2 = 1, х2 + у2 = 9, х = 0, у = 0, (
 ),
),
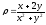 .
. -
s: х2 + у2 = 1, х2 + у2 = 16, х = 0, у = 0, (
 ),
),
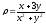 .
. -
s: х2 + у2 = 1, х2 + у2 = 4, х = 0, у = 0, (
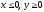 ),
),
 .
. -
s: х2 + у2 = 1, х2 + у2 = 4, х = 0, у = 0, (
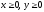 ),
),
 .
. -
s: х2 + у2 = 9, х2 + у2 = 25, х = 0, у = 0, (
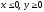 ),
),
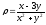 .
. -
s: х2 + у2 = 1, х2 + у2 = 9, х = 0, у = 0, (
 ),
),
 .
. -
s: х2 + у2 = 4, х2 + у2 = 9, х = 0, у = 0, (
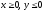 ),
),
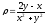 .
. -
s: х2 + у2 = 1, х2 + у2 = 25, х = 0, у = 0, (
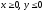 ),
),
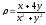 .
. -
s: х2 + у2 = 4, х2 + у2 = 25, х = 0, у = 0, (
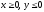 ),
),
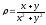 .
. -
s: х2 + у2 = 4, х2 + у2 = 16, х = 0, у = 0, (
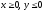 ),
),
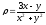 .
. -
s: х2 + у2 = 9, х2 + у2 = 16, х = 0, у = 0, (
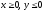 ),
),
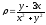 .
. -
s: х2 + у2 = 4, х2 + у2 = 9, х = 0, у = 0, (
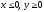 ),
),
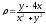 .
. -
s: х2 + у2 = 1, х2 + у2 = 4, х = 0, у = 0, (
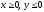 ),
),
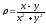 .
. -
s: х2 + у2 = 4, х2 + у2 = 9, х = 0, у = 0, (
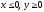 ),
),
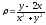 .
.