
- •Розділ ііі. Молекулярна фізика і термодинаміка Лекція 1. Молекулярно-кінетична теорія речовини
- •1. Атомно-молекулярна будова речовини.
- •Лекція 2. Елементи статистичної фізики.
- •1. Розподіл молекул ідеального газу за їхніми швидкостями.
- •2. Барометрична формула, розподіл Больцмана.
- •3. *Зіткнення молекул, середня довжина вільного пробігу молекул.
- •4. *Поведінка газів за умов низького тиску.
- •5. *Вакуумна техніка.
- •Лекція 3. Основи термодинаміки.
- •2. Внутрішня енергія системи як функція стану.
- •3. Перше начало термодинаміки.
- •4. Термодинамічні діаграми.
- •5. Ізопроцеси в газах.
- •6. Адіабатний процес.
- •Для адіабатного процесу,
- •7. Теплоємність газів.
- •Лекція 4. Друге начало термодинаміки
- •1. Термодинамічні цикли, робочі цикли теплових та холодильних машин.
- •2. Цикл Карно.
- •3. Оборотні та необоротні процеси.
- •4. Ентропія. Друге начало термодинаміки та його статистичне розуміння. *Теорема Нернста.
- •Лекція 5. Реальні гази
- •Лекція 6. Тверді тіла. Рідини
Лекція 2. Елементи статистичної фізики.
Розподіл молекул ідеального газу за їхніми швидкостями.
Барометрична формула, розподіл Больцмана.
*Зіткнення молекул, середня довжина вільного пробігу молекул.
*Поведінка газів за умов низького тиску.
*Вакуумна техніка.
1. Розподіл молекул ідеального газу за їхніми швидкостями.
Через хаотичний
рух молекул та їх взаємні зіткнення,
швидкість кожної молекули постійно
змінюється як за величиною, так і за
напрямом. В газі будуть як швидкі, так
і повільні молекули. Хоча швидкості
окремих молекул змінюються, властивості
газу в цілому у стані термодинамічної
рівноваги (![]() )
не змінюються, тобто макропараметри
системи (
)
не змінюються, тобто макропараметри
системи (![]() ,
,![]() )
залишаються сталими.
)
залишаються сталими.
Дж. Максвелл
теоретично розв’язав задачу про розподіл
молекул ідеального газу за швидкостями
поступального руху. Він встановив закон,
що дає змогу визначити, яка кількість
молекул
![]() із загальної кількості
із загальної кількості![]() молекул ідеального газу мають при даній
температурі швидкості, що лежать в
інтервалі від
молекул ідеального газу мають при даній
температурі швидкості, що лежать в
інтервалі від![]() до
до![]() .
.
Дж. Максвелл припускав, що газ складається з великої кількості n однакових молекул, температура в усіх частинах посудини з газом стала і зовнішні дії на газ відсутні.
Якщо температура газу не змінюється, то характер розподілу молекул за швидкостями знаходиться у стані рівноваги, тобто встановлюється стаціонарний незмінний у часі процес, що описується статистичним законом. Цей закон вперше отримав Дж. Максвел:
![]() –розподіл
Максвела,
–розподіл
Максвела,
де
![]() – маса молекули,
– маса молекули,
k
– стала Больцмана
![]() ,
,
![]() –швидкість
молекули,
–швидкість
молекули,
![]() –функція
розподілу молекул за швидкостями,
яка дозволяє визначити кількість
молекул, швидкість яких лежить в інтервалі
від
–функція
розподілу молекул за швидкостями,
яка дозволяє визначити кількість
молекул, швидкість яких лежить в інтервалі
від
![]() до
до![]() :
:
![]() .
.
Н
![]()
![]()
![]()
![]() .
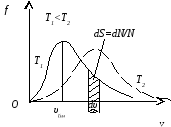
Функція
.
Функція![]() зростає від нульового до максимального
значення, а потім асимптотично спадає
до нуля. Крива несиметрична відносно
максимального значення
зростає від нульового до максимального
значення, а потім асимптотично спадає
до нуля. Крива несиметрична відносно
максимального значення![]() .
Максимум функції
.
Максимум функції![]() залежить від температури
залежить від температури![]() і роду газу
і роду газу![]() .
При збільшенні температури (або зменшенні
маси молекул) максимум кривої
.
При збільшенні температури (або зменшенні
маси молекул) максимум кривої![]() зміщується у бік більших швидкостей, а
його абсолютна величина зменшується,
причому площа, яка охоплена кривою
зміщується у бік більших швидкостей, а
його абсолютна величина зменшується,
причому площа, яка охоплена кривою![]() і віссю
і віссю![]() ,
залишається незмінною.
,
залишається незмінною.
Відносна кількість
молекул
![]() ,
швидкості яких лежать в інтервалі від
,
швидкості яких лежать в інтервалі від![]() до
до![]() ,
чисельно дорівнює площі заштрихованої
ділянки на рисунку.
,
чисельно дорівнює площі заштрихованої
ділянки на рисунку.
Швидкість
![]() ,
яку мають найбільша кількість молекул
за даної температури називаютьнайбільш
ймовірною швидкістю.
,
яку мають найбільша кількість молекул
за даної температури називаютьнайбільш
ймовірною швидкістю.
![]() ,
,
оскільки
![]() ,
,
![]() .
.
Середня арифметична
швидкість молекул
![]() визначається за формулою:
визначається за формулою:
 .
.
Отже, є три швидкості, які характеризують стан газу:
|
Найбільш
ймовірна швидкість
|
Середня арифметична
швидкість
|
Середня квадратична
швидкість
|
|
|
|
|
2. Барометрична формула, розподіл Больцмана.
З а
відсутності дії зовнішніх сил,
молекули рівномірно розподіляються по
всьому об’єму посудини. Молекули
будь-якого газу завжди перебувають в
полі сил тяжіння Землі. Якщо б не було
гравітаційного тяжіння, то молекули
повітря земної атмосфери розсіялися
по всьому Всесвіту. Але якщо молекули
повітря земної атмосфери не перебували
б у тепловому русі, то всі вони “впали”
б на Землю. Тяжіння i тепловий рух
приводять до стаціонарного стану газу,
при якому його тиск i концентрація
зменшується з висотою.
а
відсутності дії зовнішніх сил,
молекули рівномірно розподіляються по
всьому об’єму посудини. Молекули
будь-якого газу завжди перебувають в
полі сил тяжіння Землі. Якщо б не було
гравітаційного тяжіння, то молекули
повітря земної атмосфери розсіялися
по всьому Всесвіту. Але якщо молекули
повітря земної атмосфери не перебували
б у тепловому русі, то всі вони “впали”
б на Землю. Тяжіння i тепловий рух
приводять до стаціонарного стану газу,
при якому його тиск i концентрація
зменшується з висотою.
Тиск ідеального газу, що знаходиться в однорідному полі тяжіння за умови сталості температури газу змінюється з висотою за експоненціальним законом, який називають барометричною формулою (П. Лаплас, 1821 р.):
![]() .
.
Із цієї формули
можна зробити висновок, що тиск газу
зменшується із висотою експоненціально
і тим швидше, чим важчий газ (чим більше
![]() )
і чим нижча температура (див. рис.).
)
і чим нижча температура (див. рис.).
Барометрична формула дозволяє знайти співвідношення між концентраціями газу на різній висоті.
Використаємо
рівняння стану ідеального газу у
вигляді
![]() ,
де
,
де![]() –
концентрація молекул газу. При
–
концентрація молекул газу. При![]() отримуємо
отримуємо
![]() ,
,
де
![]() – концепція молекул на висоті
– концепція молекул на висоті![]() ,
а скільки
,
а скільки![]() ,
а
,
а![]() ,
то
,
то
![]() .
.
Якщо молекули, що перебувають у стані хаотичного теплового руху, знаходяться у зовнішньому потенціальному полі (наприклад, у полі тяжіння Землі), то розподіл молекул описується законом Больцмана:
![]() або
або
![]() –розподіл
Больцмана,
–розподіл
Больцмана,
де
![]() – концентрація молекул на висоті
– концентрація молекул на висоті![]() (
(![]() ),
),
![]() –концентрація
молекул на висоті
–концентрація
молекул на висоті
![]() =0м,
=0м,
μ – молярна маса газу,
![]() –висота над
поверхнею землі,
–висота над
поверхнею землі,
![]() –потенціальна
енергія молекули (наприклад, у полі
тяжіння Землі).
–потенціальна
енергія молекули (наприклад, у полі
тяжіння Землі).
Із
закону Больцмана випливає, що
у полі тяжіння Землі:
із збільшенням висоти концентрація молекул газу зменшується за експоненціальним законом,
при високих температурах концентрація молекул n незначно зменшується з висотою і при

 ,
тобто підвищення температури викликає
вирівнювання концентрації газу за
висотою,
,
тобто підвищення температури викликає
вирівнювання концентрації газу за
висотою,при

 ,
тобто всі молекули під дією сили тяжіння
опускаються на дно посудини.
,
тобто всі молекули під дією сили тяжіння
опускаються на дно посудини.
