5.2. Модель угловых коэффициентов

5.2.1 (0,3,3) СХЕМА ПОЛНОЙ РАНДОМИЗАЦИИ Количественное определение активности фактора VIII

Предположим, в лаборатории выполняют количественное определение активно­сти фактора VIII в концентратах по образованию окрашенного продукта. Предположим также, что лаборатория не имеет опыта в проведении количественного определения подобного рода, но тем не менее попыталась выполнить эту процедуру. Готовят по три эквивалентных разведения для стандартного и испытуемого препаратов. Дополни­тельно готовят препарат «плацебо», хотя и не ожидается наличия линейной зависимо­сти эффекта от дозы в области малых доз. Число повторений для каждого из разведе­ний равно восьми, что несколько больше, чем требуется при выполнении ежедневных количественных определений.

Графическое представление данных показывает, что зависимость результата от дозы действительно не линейна в области малых доз. На этом основании результаты, полученные при анализе препарата «плацебо», не будут использоваться при расчетах ( в дальнейшем для подтверждения данного решения, безусловно нужно будет провес­ти повторные определения с препаратом «плацебо»). Используя формулы, приведен­ные в Таблицах 3.3.3.1-1 и 3.3.3.1.-2, получаем следующие результаты:

Ps = 0,6524 Pt = 0,5651

Ls = 1,4693 Lt = 1,2656

as = 0,318 a_t = 0,318

bs = 0,329 Ьт = 0,271

Gs = 0,1554 Gt = 0,1156

Js = 4,17х10^-8 Jt = 2,84х10^-6

и

Hi = 0,09524 a' = 0,05298 K = 1,9764

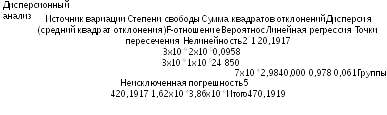
Далее выполняют дисперсионный анализ по формулам, приведенным в Табли­цах 3.3.3.1.-3 и 3.3.3.1.-4.

Высокая значимость регрессии и отсутствие значимых отклонений от линейности и точки пересечения оси ординат, дают основание для расчета активности.

Угловой коэффициент стандартного препарата b_s = ^{6 х 1,469 - 36 х 0,0530} = 00822

^s 84 Угловой коэффициент испытуемого препарата b_T = ^{6 х1.266 - 36 х 0,0530} = 00677

По формуле 3.3.5.1.-3 получаем R = ⁰⁰⁶⁷⁷ = 0823

0 0822

0 0822²

c

0,0822² - 3,86 ■ 10^-6 x 2,018² x 0,0357 k = 0,000083 x 0,75 = 0,000062

=1 000083

а 95% доверительный интервал равен

0823 ±j0,000083 x 1,678 + 0,000062 x (-1,646) = 0,823 ± 0,006

Таким образом, полученная активность равна 0,823 с 95% доверительным ин­тервалом от 0,817 до 0,0826.

Таблица 5.2.1.-1.

T2

0,02 0,188 0,188 0,190 0,190 0,190 0,191 0,191 0,190 0,1898

T3

0,03 0,254

0,253 0,255 0,258 0,257 0,257 0,255

0,254 0,2554

Испытуемый препарат T (в МЕ/мл)

Показатели оптической плотности

S1 0,01 0,133 0,133 0,131 0,136 0,137 0,136 0,138 0,137 0,1351

S2

0,02 0,215

0,215 0,216 0,218 0,220 0,220 0,219

0,218 0,2176

Стандартный препарат S (в МЕ/мл)

S3 0,03	T1 0,01
0,299	0,120
0,299	0.119
0,299	0,118
0,297	0,120
0,297	0,120
0,305	0,121
0,299 0,302	0,121 0,121
0,2996	0,1200

5.2.2 (0,4,4,4) СХЕМА ПОЛНОЙ РАНДОМИЗАЦИИ

Количественное определение активности вакцины против гриппа in vitro

Содержание антигена гемаглютинина (НА) в двух вакцинах против гриппа опре­деляли методом радиальной иммунодиффузии. На этикетках обеих вакцин была ука­зана активность 15 мкг НА на одну дозу, что эквивалентно содержанию 30 мкг НА/мл. Стандартный препарат имел установленную активность 39 мкг НА/мл.

Исследовали четыре концентрации стандартной и испытуемой вакцин, рассчи­танных исходя из предполагаемых и обозначенных на этикетке активностей; в каждом случае число повторений равно двум. После установления равновесия между внутрен­ним и внешним реагентами, измерялась площадь кольцевых зон осадка. Результаты приведены в Таблице 5.2.2.-1.

Графическое представление данных не выявило никаких необычных особенно­стей расположения данных.

Используя формулы, приведенные в Таблицах 3.3.3.1-1 и 3.3.3.1.-2, получаем

и

Hi = 0,0093 a' = 11,04 K = 14785,8

Далее выполняют дисперсионный анализ по формулам, приведенным в Табли­цах 3.3.3.1.-3 и 3.3.3.1.-4. Результаты представлены в Таблице 5.2.2.-2.

Высокая значимость регрессии и отсутствие значимых отклонений от линейности и точки пересечения позволяют рассчитать активность.

Угловой коэффициент стандартного препарата bs = ^{6 х 3011} - ^{60 х 11,04} = ^S 180

Угловой коэффициент испытуемой вакцины Т

Ь'т

6 х 292,1 - 60 х 11,04 180

6,056

Угловой коэффициент испытуемой вакцины U

U

6 х 234,1 - 60 х11,04 180

4 123

В результате получаем следующие отношения активностей 6,056/6,356=0,953 для вак­цины Т и 4.123/6.356=0,649 для вакцины U.

C = ₂ ⁶³⁵⁶² ₂ = 10056

6,356² -1,068 х 2,179² х 0,0444

K = 0,0056 х 0,625 = 0,0035

Доверительные интервалы вычисляют по формуле 3.3.5.1.-4. Для вакцины Т

0,955 ± V0,0056 х 1,913 + 0,0035 х (-1,913) = 0,955 ± 0,063 Для вакцины U

0,649 ±70,0056 х 1,423 + 0,0035 х (-1,301) = 0,649 ± 0,058

Содержание НА в 1 мл вакцины находят путем умножения отношения активно­стей и доверительных интервалов на предполагаемую активность 30 мкг/мл. Результа­ты приведены в Таблице 5.2.2.-3.

Концентра­ция ( мкг/мл) 7,5

15,0 22,5

30,0

Площадь зоны осадка (мм²)

I

18,0 22,8

30,4

35,7

II

18,0 24,5 30,4

36,6

Стандартный препарат S

I

15,1 23,1 28,9

34,4

Испытуемый препарат T

II

16,8 24,2 27,4

37,8

Таблица 5.2.2.-1.

I

15,4 20,2 24,2

27,4

Испытуемый препарат U

II

15,7

18,6 23,1

27,0

40-

^яз 35-

3"

§■30-

25-

15-

10-

го 20­3" о ц

5 -

0

Рисунок 5.2.2.-1.

Таблица 5.2.2.-2.