Згинаючі моменти ;

(тут стрибок)

На ділянці 2-3 .

Отже, епюра Q на ділянці - пряма, паралельна вісі.

У перерізі 3 справа ;

4 справа ;

Будуємо епюру M . Поле епюри

Мірило епюри M:

Перевіряємо вірність побудови епюр. Видно, що зосереджені моменти не викликають ніяких змін в епюрі Q . У перерізах, де прикладені зосереджені моменти, на епюрах M є "стрибки" на величину цих моментів.

Зауваження. Слід відзначити, що епюра M легко може бути побудова­на так званим "векторним" способом.

Завдання № 3. Побудувати епюри Q та M для консольної балки, навантаженої зосередженими силами та моментами (навантаження задані цифровими значеннями - мал.20).

Приклад рішення

1.Поперечні сили:

; ;

.

Епюра Q . Поле епюри - 40 мм

Мірило

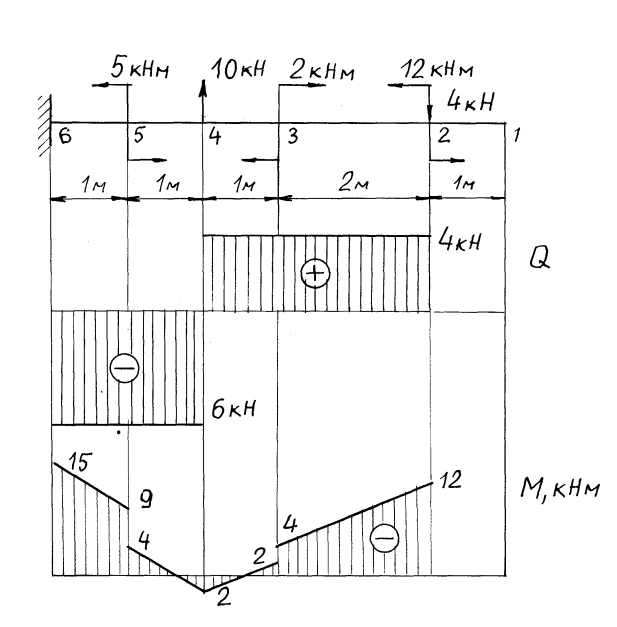
Мал.20

2.Згинаючі моменти

; ;

; ;

;

; ;

.

Епюра М .Поле епюри: - 42,5мм.

Мірило

Небезпечним є переріз 6 (защемлення), для якого , .

Завдання 4.Побудувати епюриQтаMдля балки, навантаженої зосередженою силою, моментом та рівномірно розподіленим навантаженням по схемі на мал.21.

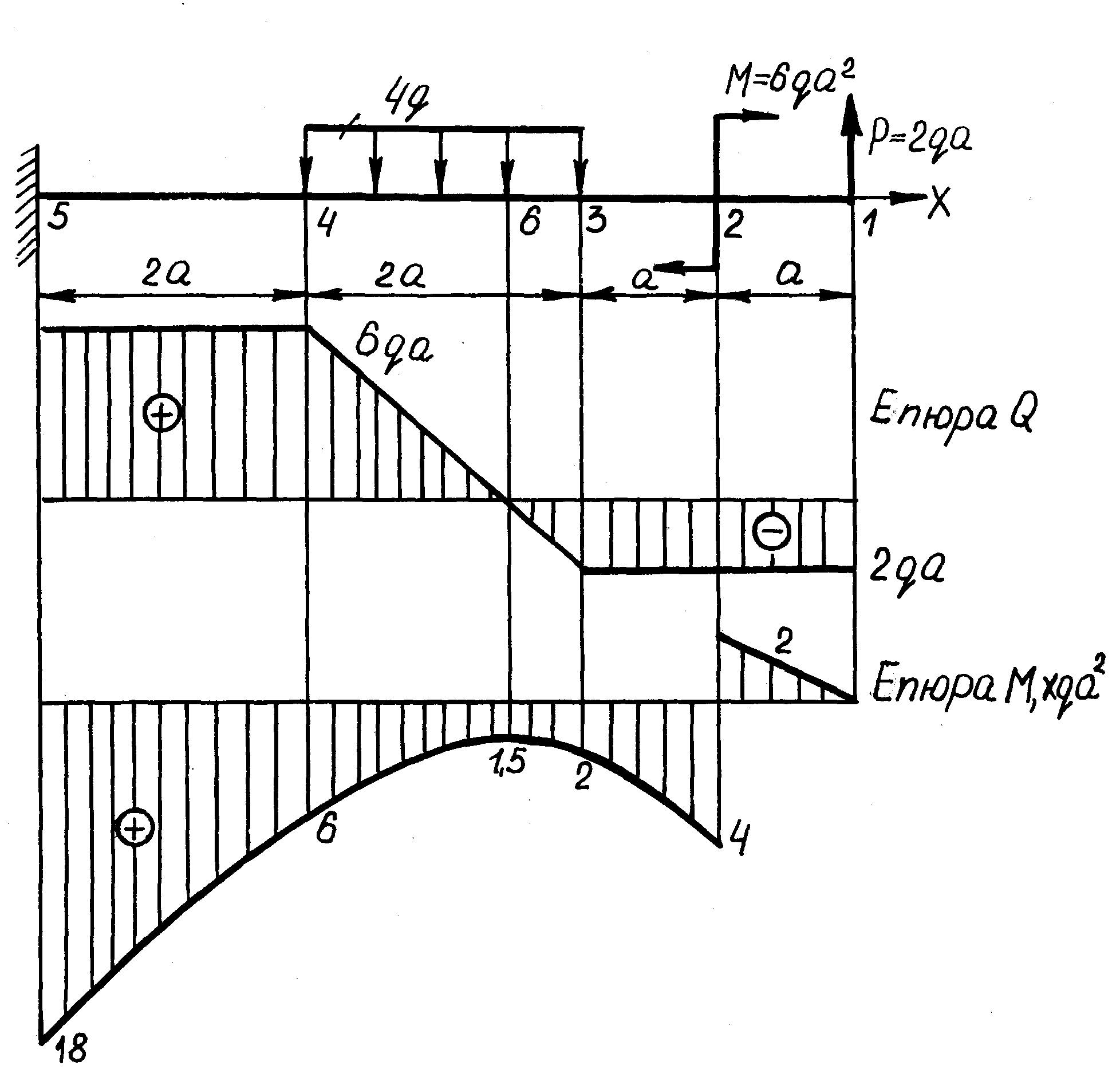
Мал.21

Відмічаємо характерні перерізи балки точками 1 5. Будемо розглядати праві від перерізу частини балки, оскільки зліва опорні реакції невідомі. Визначаємо поперечні сили

; .

Епюра Q .Поле епюри

Мірило .

Зауважимо, що епюра Q на дільниці з розподіленим навантаженням пере- тинає базис, тобто поперечна сила дорівнює нулю, а епюра M у цьому перерізі повинна мати екстремум. Переріз, відповідний , позначимо точкою 6.

Визначаємо згинаючі моменти.

; ; ;

; ;

;

Визначаємо закон зміни згинаючого моменту на ділянці 3-4 з рівномірно розподіленим навантаженням. Для довільного перерізу на відстані х від перерізу 3 згинаючий момент дорівнює

;

Одержаний вираз є рівнянням другого ступеню та графічно зобра­жується параболою. Для побудови епюри на цій ділянці необхідно визна­чити величини згинаючих моментів для кількох перерізів ; практично результат виходить задовільним, якщо взяти крім крайніх перерізів ділянки з розподіленим навантаженням ще один переріз.

Придаючи змінній значення x=0 та x=2a , одержимо значення моментів на кінцях ділянки в точках 3 та 4.

Третім перерізом в даному випадку краще всього взяти той, у якому поперечна сила Qдорівнює нулю. У цьому перерізі згинаючий момент приймає екстремальне значення. Визначимо абсцису епюри екст­ремального значення згинаючого моменту, відповідного нульовому зна­ченню поперечної сили:

; ;

Зауваження. Координата нульового значення епюри поперечних сил на цій дільниці може бути визначена різними способами , а саме:

а) на основі розгляду подібності трикутників (мал.21)

б) з рівняння рівності нулю поперечної сили для лівої чи пра­вої частини балки ;

в) з диференційних залежностей між Q та q.

Останній спосіб найбільш простий. З диференційних залежностей

і ;

де - кут нахилу епюри поперечних сил на даній дільниці (мал.22), звідки

або

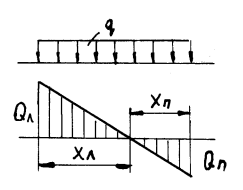
Мал. 22 абоТаким чином, відстань до нульової точки епюри поперечних сил дорівнює відношенню ординати епюри до величини інтенсивності рівномірно розподіленого навантаження:

або

Екстремальне значення згинаючого моменту у перерізі 6

По трьох точках можлива побудова параболи.

Будуємо епюру М. Поле епюри:.

Мірило .

Відкладаючи знайдені ординати та з'єднуючи послідовно точки відповідно з законом зміни моменту в межах ділянок одержуємо епюру М. Епюра дає можливість визначити величини згинаючих моментів у будь-якому перерізі, треба тільки виміряти ординату, відповідну даному перерізу і помножити на мірило епюри.

Перевірка вірності побудови: для додатних значень епюри Q спостерігається зростання значень епюри моментів, а для від'ємних - спад; у перерізі 2 під зосередженим моментом є стрибок ; по іншим критеріям відповідність також зберігається.

Небезпечний переріз буде у защемленні, де абсолютна величина згинаючого моменту найбільша . У цьому перерізі найбільша поперечна сила, яка дорівнює .

Завдання 5. Побудувати епюри Q та M для двохопорної балки, навантаженої по схемі на мал.23.

Позначимо опори балки А і В та відмітимо характерні перерізи точками 1+5 (зліва-направо). Рівнодіючі розподілених навантажень прикладені на серединах ділянок 1-2 та 4-5, тобто на відстані a від опор. Величини їх дорівнюють і .

Так як навантаження прикладені перпендикулярно до вісі балки, тоді на опорах можуть виникнути тільки вертикальні складові реакцій. Приймемо , що реакція спрямована угору, а - вниз. Визначимо опорні реакції. Із рівняння моментів відносно точки А

Знаходимо .

Від'ємний знак реакції свідчить про те, що напрям її вибрано невірно.

47