Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Киевский национальный университет технологий и дизайна

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Metodichka_dlya_zaochnik_2_sem (1)

.pdf

Скачиваний:

Добавлен:

04.02.2016

Размер:

515.54 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 44

Приклад 42.	Знайти частинний	розв’язок диференціального					рівняння
y′′−3y′+ 2 y = 4sin 2x , який задовольняє початковим умовам: y (0)= −1,							y′(0)=1.
Розв’язання. Відповідне однорідне рівняння
	y′′−3y′+ 2 y = 0 ,
його характеристичне рівняння k 2 −3k + 2 = 0 , корені якого				k	= 2, k	2	=1, отже
				1		2
загальний розв’язок однорідного рівняння має вигляд
	y = C e2 x +C		ex .
	1	2
Тепер, оскільки	f (x)= 4sin 2x , то згідно (56) маємо α = 0, β = 2 ; частинний

розв’язок шукаємо у вигляді

y =(Acos 2x + B sin 2x) x0 = Acos 2x + Bsin 2x .

Тут r = 0 , оскільки ±2i не є коренем характеристичного рівняння. Тепер диференціюємо y двічі:

y′ = −2 Asin 2x +2B cos 2x; y′′ = −4Acos 2x −4Bsin 2x.

Підставимо отримані вирази в рівняння:

−4Acos 2x −4Bsin 2x −3(−2Asin 2x +2B cos 2x)+2Acos 2x +2Bsin 2x = 4sin 2x .

Зведемо подібні члени і прирівняємо коефіцієнти при відповідних членах: cos 2x(−4 A −6B +2 A)+sin 2x(−4B +6 A +2B)= 4sin 2x

−6B −2 A = 0,		A = −3B,		A =	3		= 0,6

				5
						1
−2B +6 A = 4,	−2B −18B = 4,		B = −				= −0, 2
						5

Отже, частинний розв’язок неоднорідного рівняння є y = 0,6cos 2x −0, 2sin 2x .

Тоді загальний розв’язок неоднорідного рівняння запишемо у вигляді y = y + y = C1e2 x +C2ex +0,6cos 2x −0, 2sin 2x .

Знайдемо тепер частинний розв’язок, що задовольняє початковим умовам. Підставимо x = 0, y = −1 в розв’язок:

−1 =C1 +C2 +0,6 .

Продиференціюємо y та підставимо в отриманий вираз x = 0, y′ =1:

y′ = 2C1e2 x +C2ex −1, 2sin 2x −0, 4 cos 2x, 1 = 2C1 +C2 −0, 4.

Отже, для знаходження C1 і C2 маємо систему

−1,6 =C1 +C2 ,

1, 4 = 2C1 +C2 .

Віднімемо від другого рівняння системи перше:

1, 4 +1,6 = 2C1 −C1 +C2 −C2 3 =C1 ,

отже, з першого рівняння тоді

C2 = −1,6 −C1 = −4,6.

Запишемо остаточну відповідь: частинний розв’язок диференціального рівняння має вигляд

y = 3e2 x −4,6 ex +0,6cos 2x −0, 2sin 2x .

КОНТРОЛЬНА РОБОТА №3

81-90. Знайти невизначені інтеграли.

81.а) ∫x2 +2 dx ;

x2 +1

г) ∫(x +2)e3x dx ;

82.а) ∫x2 −2 dx ;

x2 +2

г) ∫(x +3)e−2 x dx ;

83.а) ∫ x2 −1 dx ;

x2 +2

г) ∫2 +x dxx +1 ;

84.а) ∫ 2x +1 dx ;

x2 +4

г) ∫(x +3)sin 2xdx ;

85.а) ∫ 2x2−+x5 dx ;

г) ∫(x −3)cos 2xdx ;

86.а) ∫ 1+2x dx ;

x2 −5

г) ∫x ln (x +5)dx ;

87.а) ∫ 2x2−−x6 dx ;

г) ∫ln (x2 +2)dx ;

б) ∫

;

в) ∫

;

x2 +4x −3

2 + x

д) ∫(sin 5x +e−5 x

+ tg 3x −5)dx .

б) ∫

;

в) ∫

xdx

;

x2 +2x +11

1+ x −1

д) ∫(cos 4x +e4 x −ctg 2x −9)dx .

б) ∫

;

в) ∫(x +3)e2 x dx ;

x2 −2x +9

д) ∫(cos 6x −tg 3x +24 x −7)dx .

б) ∫

;

в) ∫

x dx

;

x2 −4x +7

3 + x +1

д) ∫(tg 3x −e4 x +cos3x −3)dx .

б) ∫

в) ∫

x dx

;

x2 +6x +11

1+ x +4

д) ∫(ctg 2x −e−2 x

+sin 5x +3)dx .

б) ∫

в) ∫

x dx

;

x2 −6x +10

1+ x +3

д) ∫(sin 3x −cos 4x +e−4 x + tg 2x −1)dx .

б) ∫	dx	;	в) ∫	x dx	;
	x2 +8x +17			3 + x + 2

д) ∫(tg 3x −cos3x +e3x −3)dx .

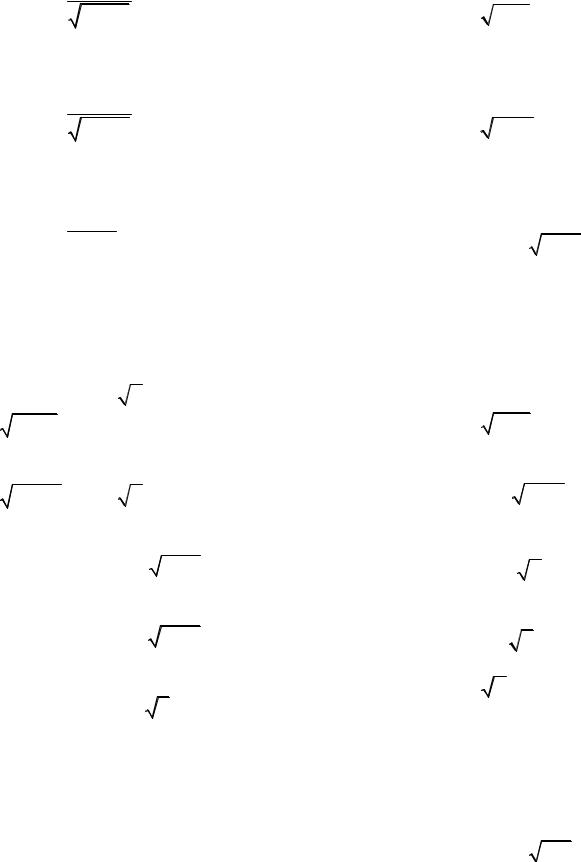
88.а) ∫ 4x2−+x6 dx ;

г) ∫xsin 5xdx ;

89.а) ∫ xx2+−42 dx ;

г) ∫arctg 2xdx ;

90.а) ∫x2 +7 dx ;

x2 +6

г) ∫arcctg 3x dx ;

б) ∫	dx	;		в) ∫		x dx		;
	x2 −8x +18					4 + x +1
д) ∫(ctg 4x −cos 4x +e−4 x					+4)dx .
б) ∫	dx				∫	x dx
			;	в)					;
	x2 +10x + 26					4 − x +2
д) ∫(sin 5x −tg 5x −e−5 x +5)dx .
б) ∫	dx		;			в) ∫	xdx			;
	x2 −10x +27						4 + x −2

д) ∫(cos 6x +ctg 6x −e6 x −6)dx.

91-100. Обчислити визначені інтеграли.

91.

а) ∫1

x dx

;

б)

∫4

x dx

96. а)

π∫sin 4x dx ;

б)

∫3

x +

0 3 + x

x +1 +2

92.

а) ∫2

x dx

;

б)

∫9

x +1

dx .

97. а)

∫1 e3x dx ;

б)

∫1

x +2

x +

−7 3 + 2 − x

а) ∫3

∫1

∫9

93.

;

б)

98. а)

∫2

tg 2x dx ;

б)

1 2x −7

−2 4 + x +3

0 12 +

x dx

а) ∫

∫

94.

;

б)

99. а) ∫ctg

dx ;

б)

∫

9 +

−1

2 + x +5

95.

dx .

x dx

а) ∫cos3x dx; б)

∫

100. а) ∫2 dx ;

б) ∫

0 4 + x

x +8

101-110. Обчислити невласні інтеграли або довести їх розбіжність.

∞

x dx

∞

x dx

∞

101. ∫0

102. ∫0

103. ∫0

104. ∫e

2x +5

x2 +3

x2 +4

ln x

+∞

∞

x dx

105.

−∞∫

106.

∫e

107. ∫1

108. ∫1

x2 +2x +9

x 3 ln x

3x +1

x2 +6

∞

109.

∫e

110.

∫0

x ln2 x

x2 +7

111. Обчислити площу фігури, яка обмежена лініями y = 3 − x2 та

y =3 − 3x .

112. Обчислити площу фігури, яка обмежена лінією ρ = 2 +cosϕ .

113. Обчислити площу фігури, яка обмежена лініями xy = 3, x =1, x = 3 ,

y= 0 .

114.Обчислити площу фігури, яка обмежена лінією ρ = 2 +sinϕ .

115.Обчислити площу фігури, яка обмежена лініями x =3y2 , y = 3x .

116.Обчислити площу фігури, яка обмежена лінією ρ = 3 −cosϕ .

117. Обчислити площу фігури, яка обмежена лініями x = 4 y2 , x = 4 y .

118.Обчислити площу фігури, яка обмежена лінією ρ = 3 −sinϕ .

119.Обчислити площу фігури, яка обмежена лініями 4 y = x2 , y = x .

120.Обчислити площу фігури, яка обмежена лінією ρ = 3 +cosϕ .

121. Обчислити довжину дуги лінії x =8sin t +6cos t, y = 6sin t −8cos t ,

0 ≤t ≤ π2 .

122. Обчислити об’єм тіла, яке утворюється при обертанні навколо осі Ox лінії y = sin x, 0 ≤ x ≤π .

123. Обчислити довжину дуги лінії x = 2(t −sin t ), y = 2(1−cost ),

0 ≤ t ≤ 2π .

124. Обчислити об’єм тіла, що утворюється обертанням навколо осі Oy

фігури, яка обмежена лініями xy = 4, y =1, y = 4, x = 0 .

125.Обчислити довжину дуги лінії y =ln cos x, 0 ≤ x ≤ π4 .

126.Обчислити об’єм тіла, яке утворюється обертанням навколо осі Oy

фігури, яка обмежена лініями x = 2 y, x = 3 − y, x = 0.

127.Обчислити довжину дуги лінії y = ln sin x, π4 ≤ x ≤ π2 .

128.Обчислити об’єм тіла, яке утворюється обертанням навколо осі Ox

фігури, яка обмежена лініями y = x3 , y = 0, x = 2 .

129. Обчислити довжину дуги лінії x =3(t −sin t ), y =3(1−cost), 0 ≤ t ≤ 2π . 130. Обчислити об’єм тіла, яке утворюється при обертанні навколо осі Ox

фігури, яка обмежена лініями x = y2 , x = 4, y = 0 .

КОНТРОЛЬНА РОБОТА №4


131-140. Знайти частинні похідні			∂z ,	∂z		,	∂2 z	функції z = f (x, y).
131-140. Знайти частинні похідні			∂z ,	∂y		,		функції z = f (x, y).
			∂x	∂y			∂x∂y
131.	z = e3x−4 y2 .	132.	z = ex2 +3 y .						133.	z = 25x+2 y3 .
134.	z = 24 x2 −2 y .	135.	z = ln (x2 −5y).						136.	z = ln (3x − y2 ).
137.	z = arctg (3x − y2 ).	138.	z = arctg (x2 +4 y).
139.	z = arcsin (2x + y3 ).	140.	z = arccos (x3 −2 y).
141-150. Знайти екстремум функції z = f (x, y).
141.	z = x2 + y2 −8x −2 .		142.		z = 3x2 + y2 + 4 y +5 .
143.	z = x2 + xy + 2 y2 −5x + y .		144.		z = 5x2 − y2 + 20x +1.
145.	z = xy (1− x − y).		146.		z = xy (1+ x + y).

147.	z = x2 −2 y2 + 4 y −6x +1.	148.	z = x2 + xy + y2 −2x + y .
149.	z = x2 + y2 + 4 y +5 .	150.	z = 3x2 + y2 + xy +11x + 2 .
151-160. Знайти рівняння прямої		y = ax +b методом найменших квадратів,

користуючись таблицею значень. 151.

	x	1	2	3		4			5

	y	2,92	1,04	0,06			−0,94		−2,03
152.

	x	1	2	3		4		5

	y	1,03	3,96	6,98		10,02		12,94
153.

	x	1	2		3		4	5

	y	0,04	2,96		5,98		9,08	11,94

154.

	x	1	2	3		4		5

	y	0,06	1,98	4,02		5,96		8,08

155.

156.

	x	1	2	3		4		5

	y	0,02	3,92	7,94		12,04		15,96
157.

	x	1	2		3	4		5

	y	0,04	4,94		9,92	15,06		19,98
158.

	x	1	2	3		4	5

	y	3,98	3,02	1,96		1,08	0,02

159.

	x	1	2	3		4	5

	y	3,04	1,98	1,06		0,08	−0,96

160.

x	1	2	3	4	5

y	0,08	0,96	2,02	3,04	3,92

x	1	2	3	4	5

y	4,52	3,96	3, 48	3,02	2,54

161-170. Знайти загальний розв’язок диференціальних рівнянь.

		(		2	)	′		2			(		2	)		′		2
161.	а)		x		−1 y		+2xy		= 0 ;	б)		xy + x			y		= y		.

162.	а)	x2 y2 y′ = y +3 ;								б)	xy′+ y = x +1.

163.

а)

2 +2)y′+2xy2 = 0 ;

б) (2xy + y2 )y′ = y2 .

164.

а)

(

3x + xy2 )y′= 4 ;

б) 2xyy′ = x2 − y2 .

165.

а)

(x2 +2)y′= 2x − xy2 ;

б)

xy′+ 4 y = x4 .

166.

а)

y2 +4 =(x2 y −4 y)y′;

б)

xy′+ 2 y = x2 .

167.

а) (

+ x2 )y′=3x +3y2 ;

б)

x2 y′ = xy − y2 .

168.

а) (

+ x2 )y′= x +3xy ;

б)

y′− y = ex .

(

)

′

= x +2xy ;

′

169.

а)

1+ x

б)

= x

+ y

170.

а)

2 +2)y′= −2xy2 ;

б)

xy′+ y = x +1.

171-180. Знайти частинний розв’язок диференціального рівняння, що задовольняє початковим умовам.


171.	y′′+3y′+2 y =8x2 +4;	y (0)=1,			y′(0)= 0 .
172.	y′′−3y′+2 y =18xe−x ;	y (0)= −1,			y′(0)=1.
173.	y′′−4 y′+4 y =8cos x;	y (0)= 2,			y′(0)= −1.
174.	y′′+4 y′+4 y = x2 + x +2;		y (0)= −2, y′(0)=1.
175.	y′′−2 y′+5y =3xe2 x ;	y (0)=1, y′(0)= 0 .
176.	y′′−2 y′+15 y = −45x2 +7, 2;			y (0)= 2,		y′(0)= −2 .
177.	y′′+ y′−6 y =39sin 3x;	y (0)=3,			y′(0)= −1.
178.	y′′− y′−6 y = 27cos 2x;		y (0)=1,		y′(0)= 0.
179.	y′′+10 y′+25y = −25x2 +25;			y (0)= 4,		y′(0)=3 .
180.	y′′+4 y′+8 y =8x2 +16x +6;			y (0)= 2,		y′(0)= 0.

<<< < Предыдущая 1 2 34 / 44

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.12.2018681.47 Кб7Metod G1.doc
#
24.12.2018416.26 Кб13Metod-G2.doc
#
04.02.20161.37 Mб48Metod-Z.pdf
#
04.02.2016291.33 Кб13Metodichka po English.doc
#
15.11.2019455.68 Кб6Metodichka.doc
#
04.02.2016515.54 Кб9Metodichka_dlya_zaochnik_2_sem (1).pdf
#
05.02.20161.15 Mб15Metodichni_vkazivki_1-3_lab_roboti.pdf
#
26.11.2018527.36 Кб2Metodichni_vkazivki_dlya_zaochnikiv_z_angl_movi....doc
#
04.02.2016872.79 Кб9metodichni_vkazivki_Excel.pdf
#
24.11.2019738.3 Кб2Metodichni_vkazivki_z_vikonannya_kursovoyi_robo...doc
#
05.02.2016781.32 Кб11MetodLabMOV.pdf