Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Киевский национальный университет технологий и дизайна

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Metodichka_dlya_zaochnik_2_sem (1)

.pdf

Скачиваний:

Добавлен:

04.02.2016

Размер:

515.54 Кб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

Міністерство освіти і науки України Київський національний університет технологій та дизайну

Методичні вказівки та контрольні роботи з вищої математики

для студентів-заочників дистанційної форми навчання технологічних спеціальностей 7.0918

Київ КНУТД 2003

Основною формою навчання студентів-заочників є самостійна робота. Студентові необхідно самому працювати з підручниками, вивчати теоретичний матеріал і навчатися засвоєний матеріал застосовувати до розв’язування задач. Запропоновані методичні вказівки мають на меті допомогти студентам самостійно оволодіти курсом вищої математики. Вони складаються з програми курсу, списку рекомендованої літератури, коротких відомостей із теорії, зразків розв’язання типових задач і прикладів та задач для контрольних робіт.

ПРОГРАМА КУРСУ ВИЩОЇ МАТЕМАТИКИ

2СЕМЕСТР

1.Інтегральне числення

1.Первісна і невизначений інтеграл, властивості.

2.Невизначене інтегрування заміною змінної та частинами.

3.Стандартна техніка невизначеного інтегрування. Інтегрування з застосуванням таблиць, інтеграли, які не виражаються через елементарні функції.

4.Визначений інтеграл: означення, властивості, практичне тлумачення, прості практичні задачі.

5.Похідна інтеграла зі змінною верхньою межею. Формула Ньютона-Лейбніца.

6.Стандартна техніка визначеного інтегрування. Оцінки інтегралів. Інтегрування з застосуванням таблиць та пакетів програм.

7.Геометричні застосування визначеного інтеграла (площа фігури, довжина лінії, об’єми деяких тіл та площі поверхонь).

8.Деякі фізичні застосування визначеного інтеграла (робота, сила тиску тощо). Різні схеми застосування визначеного інтеграла.

9.Невласні інтеграли з нескінченними межами інтегрування та від необмежених функцій. Дослідження на збіжність, ознаки збіжності.

10.Наближене обчислення визначених інтегралів. Формули прямокутників, трапецій, точність формул. Застосування тейлорової формули.

2.Диференціальне числення функцій багатьох змінних

1.Означення функції n змінних. Границі повторні і кратні. Неперервність.

2.Частинні похідні. Повний диференціал. Геометричне тлумачення. Застосування. Похідна складеної функції, повна похідна.

3.Скалярне поле, похідна за напрямком, градієнт, практичне тлумачення.

4.Частинні похідні і повні диференціали вищих порядків.

5.Екстремум. Необхідні і достатні умови у випадку довільного числа змінних, гессіан.

6.Метод найменших квадратів, випадки лінійної та квадратичної залежностей.

3.Диференціальні рівняння

1.Основна термінологія. Диференціальні рівняння (ДР) першого порядку, існування і єдиність розв’язку задачі Коші. Інтегрування в квадратурах у стандартних випадках (рівняння з відокремлюваними змінними, однорідні, лінійні, Бернуллі).

2.ДР вищих порядків. Задача Коші. Крайова задача. ДР, які допускають зниження порядку.

3.Лінійна залежність та незалежність функцій. Визначник Вронського.

4.Лінійні однорідні ДР, структура загального розв’язку, розв’язування таких рівнянь зі сталими коефіцієнтами.

5.Лінійні неоднорідні ДР, структура загального розв’язку. Розв’язування методом варіації сталих.

6.Системи ДР. Задача Коші для нормальної системи. Матрична форма нормальної системи.

7.Розв’язування нормальної системи лінійних ДР зі сталими коефіцієнтами.

8.ДР в моделюванні, природничих, інженерних, економічних ситуацій.

9.Наближене розв’язування ДР, методи ітерацій, Ейлера.

ЛІТЕРАТУРА

1.Дубовик В.П., Юрик І.І. Вища математика. – К.: А.С.К., 2001.

2.Пак В.В., Носенко Ю.Л. Вища математика. – К.: Либідь, 1996.

3.Шнайдер В.Е., Слуцкий А.Н., Шумов А.С. Краткий курс высшей математики (в двух томах). – М.: Высшая школа, 1978. – Т. 1,2.

4.Пискунов Н.С. Дифференциальное и интегральное исчисление для вузов. –

М.: Наука, 1986. – Ч. 1,2.

5.Вища математика: збірник задач. Навчальний посібник. За ред. В.П. Дубовика, І.І. Юрика. – К.: Вища школа, 1999.

6.Кулініч Г.Л. Підручник з вищої математики. – Кн. 1,2. – К.: Либідь, 1996.

7.Інтегральне числення

7.1.Невизначений інтеграл

Вдиференціальному численні розв’язували таку задачу: для заданої функції знайти її похідну. В інтегральному численні розв’язують обернену задачу: по заданій похідній відновити первісну функцію.

Невизначеним інтегралом для неперервної функції f (x) називають множину всіх первісних функцій F (x) і позначають

∫ f (x)dx = F (x)+C .

Основні властивості невизначеного інтеграла:

1)∫kf (x)dx = k ∫ f (x)dx ;

2)∫(f (x)±ϕ(x))dx = ∫ f (x)dx ± ∫ϕ(x)dx .

Таблиця основних інтегралів:

∫dx = x +C ;

∫cos u du = sin u +C ;

∫uα du =

uα+1

+C,

(α ≠ −1);

∫

= tg u +C ;

α +1

cos

∫duu

= ln

+C ;

∫

= −ctg u +C ;

sin2 u

10.

= ln

+C ;

∫a

∫sin u

du = ln a +C ;

∫eu du = eu +C ;

11.

∫

= ln

tg (

+ π4 )

+C ;

cos u

∫sin u du = −cos u +C ;

12.

∫tg u du = −ln

cos u

+C ;

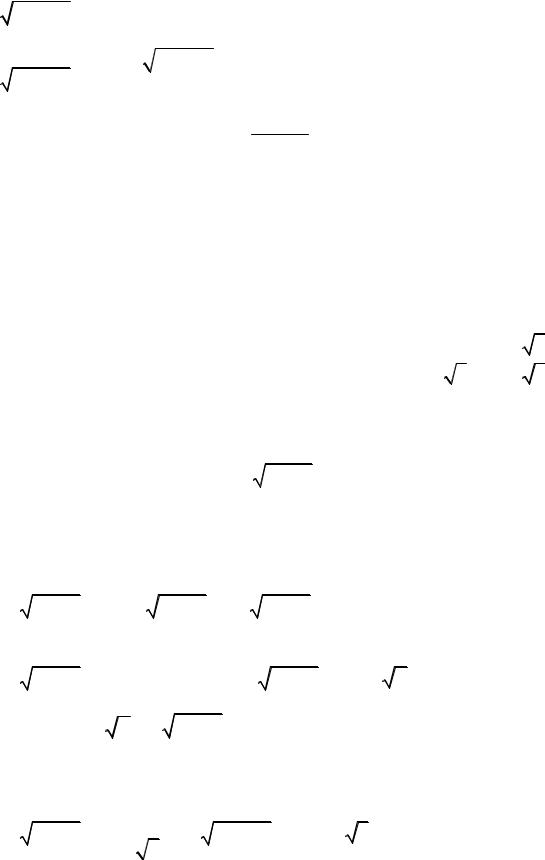
13.

∫ctg u du = ln

sin u

+C ;

16. ∫

= a arctg a +C ;

u2 + a2

14.

∫

= arcsin u

+C ;

17. ∫

u − a

+ C .

a2 −u2

u + a

u 2 − a2

15.

∫

= ln

u +

u2 +a2

+C ;

±a

Приклад 21. Знайти інтеграл ∫x22+12 dx . x −3

Розв’язання. Виділимо цілу частину підінтегральної функції. Для цього поділимо чисельник на знаменник способом ділення многочлена на многочлен, або припишемо в чисельнику −3 та +3 і розглянемо суму дробів. Одержимо

x2 −3 +3 +12

x2 −3

x2 −

−3

x2 +12

x −

dx =

dx +15

=x +

+C .

∫

−3

∫

−3

∫

∫x

−3

2 3

x +

Приклад 22. Знайти інтеграл ∫

3x −2

dx .

5 − x

Розв’язання. Розглянемо різницю двох інтегралів і до кожного із них застосуємо відповідну формулу із таблиці інтегралів. Одержимо

∫

3x −2

dx =3∫

xdx

−2∫

= I ,

5 − x2

∫

xdx

u =5 − x2

∫

−2xdx

∫

∫u

−

= −

2 du =

5 − x

= −

−2

5 − x

2xdx

= −1 u

= − u = − 5 − x2 ;

u = x

∫

du = dx

= ∫

= arcsin

;

5 − x

a =

−u

I = 3(− 5 − x2 )−2arcsin	x	+C = −3 5 − x2 −2arcsin	x	+C .
	5		5

Приклад 23. Знайти інтеграл ∫x2 +dx5x +9 .

Розв’язання. Виділимо повний квадрат у знаменнику підінтегральної функції і зможемо застосувати відповідну формулу із таблиці інтегралів. Одержимо

x2 +5x +9 =

∫

= x

5x +

= ∫

−

+9 =

x2 +5x +9

x +

= x +

u = x + 5

= ∫

2x +5

du = dx

+C =

+C.

= a arctg a

arctg

u2 +a2

a =

Приклад 24. Знайти інтеграл ∫

x −3 +5

Розв’язання. Часто доводиться вводити заміну для спрощення обчислення

інтегралу. Замінимо x −3 на нову змінну. Одержимо

∫

x dx

x −3

=t, dx = 2t dt

= ∫

(t2 +3)2t dt

x −3 +5

x −3

x =t

t +5

= 2

∫

3 +

dt = 2

∫

−5t +28 −

140

t +

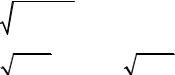
_ t3 +3t

t +5

= 2∫t2 dt −10∫t dt +56∫dt −280∫

140

t3 +5t2

t2 −5t +28 −

t +5

−10

+56t −280ln

t +5

+C =

_ −5t2 +3t

−5t2 −25t

(x −3)3 −5(x −3)+

_ 28t

28t +140

+56

x −3 −280ln

x −3 +5

+C.

−140

Приклад 25. Знайти інтеграл ∫x2 cos 2x dx .

Розв’язання. Серед методів інтегрування важливим є метод інтегрування частинами. Формула інтегрування частинами має вид

∫u dv =uv −∫v du .

(24)

При інтегруванні цю формулу застосовують один чи декілька раз. Застосуємо формулу для знаходження інтеграла:

∫x2 cos 2x dx =

u = x2 , du = 2x dx

1 x2 sin 2x −

1 ∫sin 2x 2xdx =

dv = cos 2x dx, v =

sin 2x

1 x

2 sin 2x −∫xsin 2x dx =

u = x,

du = dx

dv =sin 2x dx, v = −

cos 2x

sin 2x −

−

x cos 2x −

−

cos 2x dx =

sin 2x +

∫

cos 2x −

1 ∫cos 2x dx =

sin 2x +

cos 2x −

1 sin 2x +C.

Приклад 26. Знайти інтеграл ∫x2 ln (x +2)dx .

Розв’язання. Для знаходження інтеграла застосуємо формулу (24). Одержимо

u = ln (x +

2), du =

∫x

ln (x +2)dx

x +

ln (x

+ 2)

−∫

dv = x2 dx,

v =

_ x3

x +2

−

∫

dx =

x +2

−

+2x

−2x +4 −

x +2

_ −2x

−

3 ∫

−2x +4 −

dx =

x +2

−

x +2

−2x2 −4x

−

1 ∫x2

dx +

2 ∫x dx

− 4

∫dx

∫

_ 4x

x +

4x +8

x +2

−

3 x +

−8

+	8	ln	x +2	+C =		x3	ln	x +2			−		x3	+	x2	−	4x	+		8	ln	x +2		+C.
	8					x3							x3		x2		4x			8
	3					3							9		3		3			3
	3					3							9		3		3			3
		Приклад 27. Знайти інтеграл ∫(e−3x +ctg 5x − 3																					x +2)dx.
		Розв’язання.
		∫(e−3x +ctg 5x − 3						x +2)dx = ∫e−3x dx + ∫ctg 5x dx −∫3																	x dx + 2∫dx =
		= −1 e−3x −					1			3x		4							1 e−3x −				1				3 3
							1		−	3x		3	+2x +C = −										1			−	3 3	x4	+ 2x +C.
					5sin2 5x				−	4			+2x +C = −										5sin2 5x			−	4	x4	+ 2x +C.
		3			5sin2 5x					4									3				5sin2 5x				4

7.2. Визначений інтеграл

Для обчислення визначеного інтеграла застосовують формулу, яка зв’язує визначений інтеграл та первісну функцію. Ця формула має вигляд

∫b	f (x)dx = F (x)	b	= F (b)− F (a),	(25)
a		a

де F (x) – первісна функція, а a та b – межі (границі) інтегрування і її називають формулою Ньютона-Лейбніца.

Приклад 28. Обчислити інтеграл ∫1 e2 x dx .

Розв’язання. При обчисленні визначеного інтеграла за формулою (25)

необхідно знайти первісну функцію для функції e2 x . Одержимо

∫1 e2 x dx =	1 e2 x	1	=	1	(e2 1 −e0 )=		1	(e2	−1).
0	2	0		2			2
Приклад 29. Обчислити інтеграл				11∫	dx	.
Приклад 29. Обчислити інтеграл				11∫	x −2 +3	.
				6	x −2 +3

Розв’язання. Для знаходження первісної в заданому інтегралі необхідно застосувати метод заміни змінної. Разом із заміною змінної поміняємо межі інтегрування. Одержимо

x −

2 =t,

x =t2

+2,

при

x = 6 : t1

∫6

x −2 +3

x −2

=t2 , dx = 2t dt, при x =11: t2

(t +3)−3 dt = 2

= ∫2t dt

= 2∫

∫dt −3∫

= 2t

t +

t +3

=2(3 −2)−6(ln 6 −ln 5)= 2 −6ln 65 .

7.3.Невласні інтеграли

=6 −2 = 2, =

=11−2 = 3

−6ln t +3 =

Невласними інтегралами з нескінченними межами називають інтеграли виду

+∞∫	f (x)dx = blim→+∞ ∫b	f (x)dx,	∫b	f (x)dx = alim→−∞ ∫b	f (x)dx.	(26)
a	a		−∞	a

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.12.2018681.47 Кб7Metod G1.doc
#
24.12.2018416.26 Кб13Metod-G2.doc
#
04.02.20161.37 Mб48Metod-Z.pdf
#
04.02.2016291.33 Кб13Metodichka po English.doc
#
15.11.2019455.68 Кб6Metodichka.doc
#
04.02.2016515.54 Кб9Metodichka_dlya_zaochnik_2_sem (1).pdf
#
05.02.20161.15 Mб15Metodichni_vkazivki_1-3_lab_roboti.pdf
#
26.11.2018527.36 Кб2Metodichni_vkazivki_dlya_zaochnikiv_z_angl_movi....doc
#
04.02.2016872.79 Кб9metodichni_vkazivki_Excel.pdf
#
24.11.2019738.3 Кб2Metodichni_vkazivki_z_vikonannya_kursovoyi_robo...doc
#
05.02.2016781.32 Кб11MetodLabMOV.pdf