§ 5. Правила Кiрхгофа

Кірхгоф установив правила розв'язку задач для розгалуженого електричного кола. Розгалуженим електричним колом називається коло, в якому є 2 і більше вузлів струму. Вузол  це точка зєднання кола, де сходяться 3 і більше струмів. Наприклад, на Мал.26 представлено вузол у точці Y в яку входять струми І₁ та І₃ , а виходять струми І₂ та І₄.

П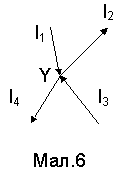ерше правило Кірхгофа. Для сталого або квазисталого струму у вузлах не відбувається накопичення зарядів і виконується закон збереження заряду. Звідси випливає перше правило Кірхгофа: сума струмів, що приходять у вузол, дорівнює сумі струмів, що виходять із вузла. Якщо струмам, що виходять із вузла приписати від'ємний знак, а струмам, що входять  додатний, то перше правило Кірхгофа можна записати у вигляді

, (1)

де алгебраїчна сума береться по всім k струмам вузла. Для наведеного на малюнку 6 прикладу, за першим правилом Кірхгофа буде

І₁ + І₃ - І₂ - І₄ = 0.

Друге правило Кірхгофа. В розгалужених колах виділяються окремі замкнені контури, вершинами яких є вузли. Кожна із сторін контуру розглядається як неоднорідна дільниця струму з потенціалами _і та _і+1, струмом І_і, опором R_і, електрорушійною силою Е_і та напругою U_i=R_iI_i. За додатній прийнято напрямок обходу контуру проти годинникової стрілки, тобто напрямок 132 для прикладу, зображеного на малюнку 27. Виведемо 2-ге правило Кірхгофа. Запишемо вирази для напруги на ділянках 1,2, 3 :

Я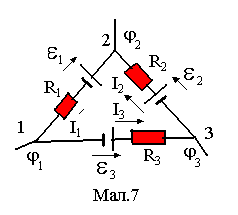кщо додати ліві та праві частини записаних рівностей, то в правій частині послідовно взаємознищуються потенціали і в результаті одержимо 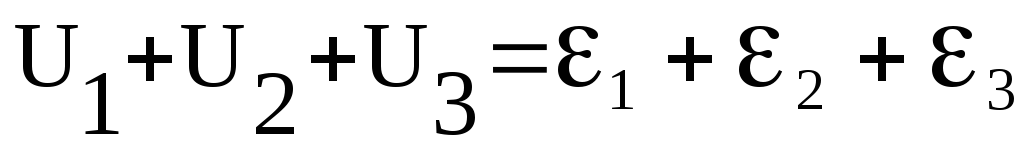. Одержана рівність

(2)

виражає друге правило Кірхгофа. В (2) напруги беруться із знаком "+", якщо відповідні їм струми за напрямком співпадають із напрямком обходу контуру, а в противному їм приписується знак "-". За додатній напрямок ЕРС береться напрямок від полюса "-" до полюса "+", як це показано на Мал.7. Знак ЕРС в правій частині (2) визначається співпаданням напрямку ЕРС із напрямком обходу (знак "+"), чи ні (знак"-"). За законом Ома U_i = I_iR_i і друге правило Кірхгофа можна записати також у вигляді

. (3)

Розв'язок електротехнічних задач на основі правил Кірхгофа. Методика розв'язування цих задач полягає в тому, що в розгалужених колах виділяються вузли й окремі замкнені контури. Вказується додатній напрям обходу контурів: проти годинникової стрілки. Далі визначаються струми та ЕРС і їх напрями на кожній зі сторін контуру. Знаки струмів та ЕРС додатні, якщо їх напрямки співпадають із напрямком обходу контуру. Для вузлів записують перше, а для контурів друге правило Кірхгофа. Таким чином можна одержати необхідну систему незалежних лінійних рівнянь відносно невідомих опорів R, струмів I та ЕРС.

Магнетизм §6. Закон Бiо - Савара – Лапласа та його застосування

Закон Бiо - Савара - Лапласа.

Біо та Савар експериментально дослідили величину індукції магнітного поля dВ, створеного елементом електричного струму dl, а Лаплас узагальнив ці дослідження, зв’язавши відповідні величини у витончену формулу

, (1)

де

,

а

є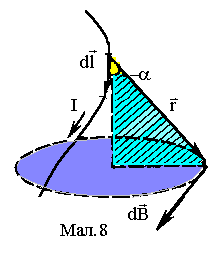магнітна стала, радіус-вектор положення точки спостереження відносно елемента струму, Ісила струму в провіднику. Напрямок задається напрямком струму. Вектор, як векторний добуток двох векторів, є векторплощині, якувони утворюють, і направлений так, що з його вершини поворот вектора донайкоротшим шляхом видно проти годинникової стрілки (див.Мал.8). Величина векторадорівнює

.

Із закону Біо-Савара-Лапласа випливає принцип суперпозиції, який визначає, що магнітне поле, створене декількома струмами, має індукцію , яка визначається векторною сумоюN індукцій , створених кожним струмомI_i окремо

.

Якщо взяти деякий провідник із струмом, то індукція магнітного поля в точці, що визначається вектором r,тепер може бути записана у вигляді

, (2)

де інтеграл береться по заданій довжині провідника із струмом з точки 1 до точки 2.

У магнітних середовищах, у порівнянні з вакуумом, величина індукції магнітного поля збільшується вразів і становить

.

Коефіцієнт називається магнітною проникливістю середовища.

Індукція є силовою характеристикою магнітного поля. Для зручності розрахунків інших характеристик поля введено поряд з індукцієюще напруженість поля, яка визначається так

. (3)

Нижче буде докладніше розглянуто визначення та зміст напруженості магнітного поля.

Магнітне поле заряду, що рухається.

Струм

(4)

в елементі провідника dl створюють dN електронів із зарядом q=е, які рухаються з дрейфовою швидкістю , причому . За законом Біо - Савара - Лапласа ці dN електронів створюють індукціюмагнітного поля, а тому індукція поля, створеного одним зарядом, може бути обчислена так

,

, .(5)

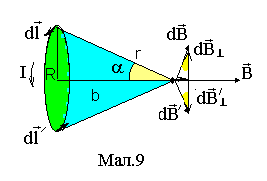
Магнітне поле колового струму.

Нехай по провіднику у вигляді кола радіусаR тече струм І. Визначимо за допомогою закону Біо - Савара - Лапласа індукцію магнітного поляВ на осі контуру в точці А, що створюється цим струмом (див Мал. 9). Виділимо два симетричних відносно центру кола елементи струму та , які створюють відповідні вектори індукції та .Ці вектори можна розкласти на складові вздовж () та поперек () осі контурута . Індукціявизначається векторною сумоюпо всім.З малюнка видно, що ця сума складається попарно із сум поперечних антипаралельних складових _,які взаємно знищуються та паралельних складових, тобто їх сума і є величиною індукції. За напрямком векторнаправлений вздовж осі контуру.Із малюнка видно,що

Тепер знайдемо величину вектора індукції

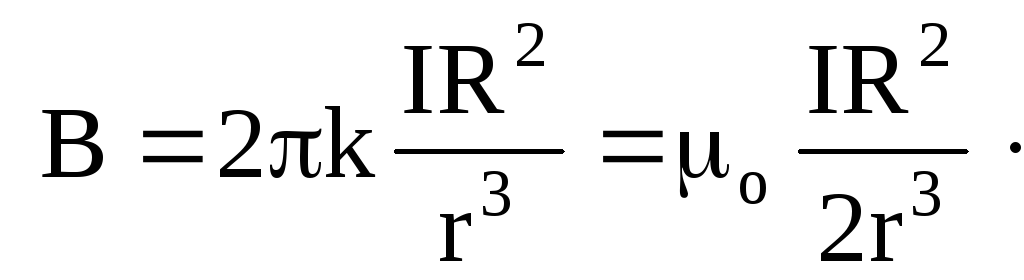(5)

Якщо точка А співпадає з центром кола, то r = R і в центрі колового струму буде

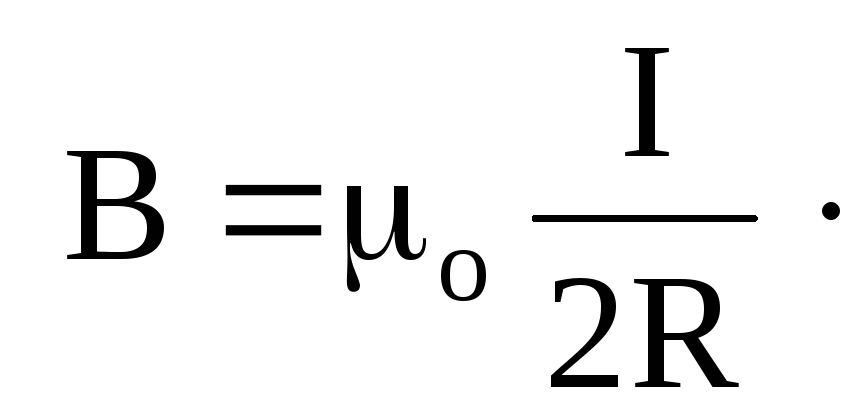(6)