Шпоры / шпоры тау / 2006 г. ЭВТд-ТАУ / 5-2005г.Метод фазовых траекторий

4

Метод фазовых траекторий

Метод удобен для исследования нелинейных систем второго порядка, когда рассматривается фазовая траектория на плоскости.

Фаза – составляющая процесса, явления, системы, состояния вещества; составляющая динамического процесса в системе.

В декартовой системе координат в качестве независимой переменной по оси абсцисс откладывается регулируемая величина y, по оси ординат –dy/dt. Для систем второго порядка (y, dy/dt) достаточно для характеристики процесса в системе.При движении системы изображающая точка (y, ) изменяет своё положение на фазовой плоскости, прочерчивая фазовую траекторию, совокупность которых называется фазовым портретом.

Анализ поведения системы по фазовому портрету:

1. Определение возможных режимов работы;

2. Суждение об устойчивости системы и ее границах;

3. Выявление автоколебательных режимов и определение их амплитуды и частоты;

4. Суждение о типе переходного процесса (колебательный или апериодический) для определённой области начальных условий;

5. Точное определение переходного процесса в системе для заданной совокупности начальных условий;

6. Оценка величины перерегулирования реакции системы на скачкообразное входное воздействие;

7. Влияние отдельных нелинейностей (сопоставление с линейными системами и нелинейными с другими нелинейностями);

8. Рекомендации по коррекции системы линейными и нелинейными средствами.

Особую точку в начале координат, на которую навёртываются все траектории, называют фокусом. Фазовую траекторию, превращающуюся в замкнутую кривую, называют предельным циклом (в системе устанавливается режим автоколебаний).

Сепаратриссы – особые фазовые траектории, разделяющие фазовый портрет нелинейной системы на области с различным видом фазовых траекторий.На фазовом портрете могут быть устойчивые и неустойчивые узлы, особые отрезки, седла, центры.

Свойства фазовых траекторий :

1. В верхней полуплоскости, где dy/dt>0, изображающая точка всегда движется слева направо (в сторону увеличения y), а в нижней – справа налево;

2. Фазовые траектории пересекают ось y под прямым углом.

Построение фазовых траекторий

САУ называется автономной, если при рассматриваемых процессах она не подвергается внешним воздействиям и не содержит параметров, изменяющихся во времени.

Если в дифференциальное уравнение второго порядка автономной системы

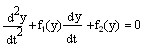
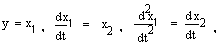
подставить то оно может быть записано в форме

системы двух дифференциальных уравнений первого порядка:

.

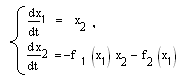Разделив почленно уравнения, получим

, решение которого-уравнение фазовой траектории. (1)

Фазовая траектория в декартовой системе координат есть интегральная кривая дифференциального уравнения (1) при заданных начальных условиях : и .

Проинтегрировав это уравнение, находим уравнение интегральной кривой на

фазовой плоскости, где с-постоянная интегрирования, определяемая из начальных условий.

Точки , в которых наклон траектории не определен, называются ОСОБЫМИ.

При построении фазовых траекторий удобно пользоваться методом ИЗОКЛИН:

положим наклон

-

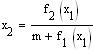тогда из (1) получим - уравнение линии, в любой из точек которой

фазовая траектория имеет один и тот же угол наклона, т.е. будет уравнением изоклины.

На фазовой плоскости наносят семейство изоклин для различных значений m, после чего вдоль каждой изоклины вычерчивают ряд параллельных отрезков с углом наклона α (tgα=m). Фазовая траектория получается построением плавной кривой, пересекающей каждую изоклину под соответствующим углом.

Построение кривой переходного процесса по фазовой траектории

Пусть имеется фазовая траектория системы. Известно, что значение координаты y во времени будет или .

Отсюда .

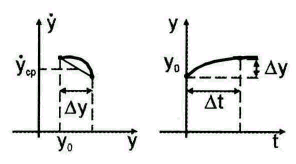
Фазовая траектория аппроксимируется прямолинейными отрезками и определяются значения в середине каждого отрезка. Проекция этого отрезка на ось y даёт . При этом

и .

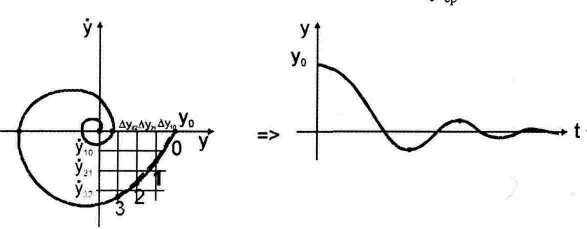
Методы вычисления времени по фазовой траектории имеют существенный недостаток: трудность точного считывания координат кривой.