14

Системы автоматического управления с ЦВМ

Литература:

1. Бесекерский В.А. Цифровые автоматические системы. М.: Наука, 1976.

2. Куо Б. Теория и проектирование цифровых систем управления. М.: Машиностроение, 1986.

3. Микропроцессорные системы автоматического управления. Под общ. ред. В.А. Бесекерского. Л.: Машиностроение, 1988.

4. Проектирование микропроцессорных систем автоматического управления. Ч.1. Синтез системы автоматического управления: Учеб. пособие/ Г.Г.Диркс, В.Г. Коломыцев; ПГТУ. Пермь, 1997.

5. Фёдоров С.М., Литвинов А.П. Автоматические системы с цифровыми управляющими машинами. М.-Л.: Энергия, 1965.

6. Теория автоматического управления. Под ред. В.Б.Яковлева. М.: Высшая школа, 2003.

7. Дорф Р., Бишоп Р. Современные системы управления. М.: Лаборатория базовых знаний. 2002.

8. Филлипс Ч., Харбор Р.Системы управления с обратной связью. М.: Лаборатория Базовых Знаний, 2001.

В многорежимных и многомерных САР, в системах с перестраиваемой структурой, многосвязных, высокоточных и многих других видах САУ получили широкое применение цифровые вычислительные машины.

ЦВМ выполняют функции задатчиков, сравнивающих устройств, устройств коррекции, автоматических регуляторов с быстроперестраиваемыми программами, коммутаторов, управляющих автоматов и других устройств.

Функциональная схема САУ с ЦВМ

АЦП обычно проектируют 10–20 разрядными, а ЦАП можно применить с пониженной разрядностью (не менее 7), так как входной сигнал ЦАП имеет малое число двоичных разрядов.

Применение микроЭВМ позволяет:

• упростить САУ путём применения простых и надёжных модулей;

• расположить цифровую вычислительную часть системы в непосредственной близости от основных элементов канала управления;

• сложную обработку поступающей информации;

• решение нескольких задач при обслуживании разных каналов управления с разделением во времени поступающей для обработки информации;

• реализовать практически любой алгоритм управления;

• осуществлять операции оптимизации САУ по статическим и динамическим показателям качества;

• проводить операции контроля и поиска неисправностей.

Структурная типовая схема ЦАС

Экстраполятор нулевого порядка

;

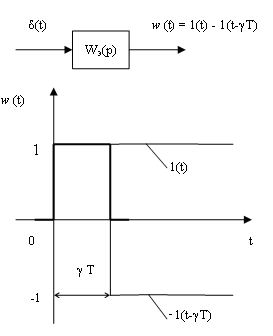
при =1- передаточная функция экстраполятора 0-го порядка.

Т – такт работы ЦВМ по преобразованию информации (0,011с).

- передаточная функция ЦВМ, учитывающая временное запаздывание сигнала при прохождении по каналу АЦП–процессор–ЦАП; учитывается в W₀(p);<<T(1мс);

k_АЦП– передаточный коэффициент АЦП;

k_ЦАП– передаточный коэффициент ЦАП;

 - (ИЭ1) идеальный импульсный элемент первого рода, который непрерывную функцию преобразует в решетчатую;

 - (ИЭ2) идеальный импульсный элемент второго рода, преобразующий решетчатую функцию y_м[n] в последовательность дельта-функций.

_{При проектировании цифровых систем автоматического управления стремятся выбрать период Т так, чтобы он был намного меньше основной постоянной времени непрерывной части системы.}

_{Период квантования Т можно определить с помощью приближенной формулы: ,}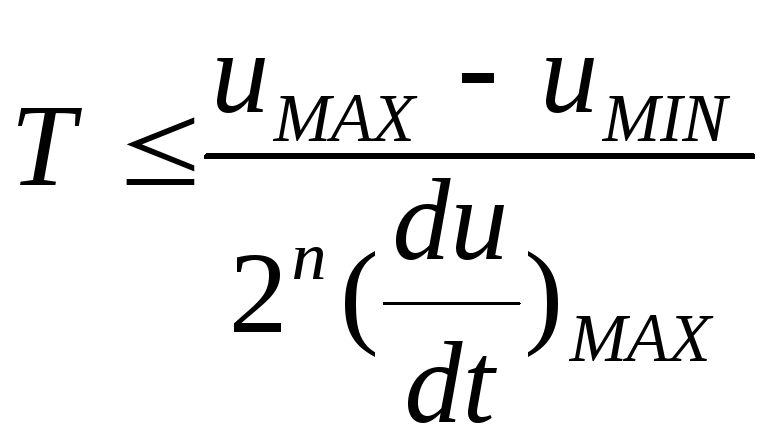

_{где n – число двоичных разрядов;}

- максимальная скорость изменения непрерывного сигнала.

Квантование по времени - важнейший признак класса цифровых систем, а квантование по уровню – нелинейных систем.

В приближенных расчетах шумами квантования по уровню и нелинейностями статических характеристик АЦП и ЦАП пренебрегают.

Математическое описание работы идеального амплитудно–импульсного элемента в пространстве Фурье

Преобразование Фурье сигнала

имеет вид ,

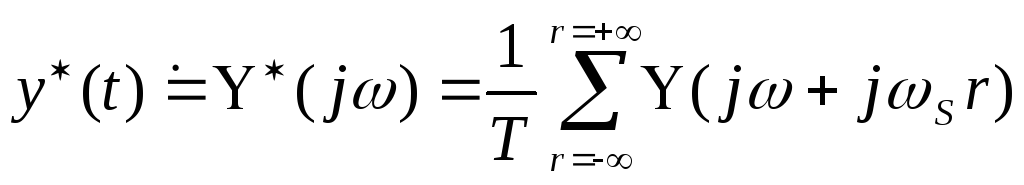где r– номер гармоники,

- частота квантования.

Неискаженная информация получается, если .

При достаточно большой частоте импульсов, образующих выходной сигнал импульсного элемента, непрерывная часть системы реагирует только на низкочастотную составляющую сигнала, несущую информацию о непрерывном сигнале на входе импульсного элемента. Дискретность работы импульсного элемента обусловливает лишь в качестве побочного явления возникновение на выходе системы высокочастотной составляющей в виде помехи, частотный спектр которой кратен частоте f=1/Tимпульсного элемента.

Условие допустимости сведения импульсной системы к непрерывной

,

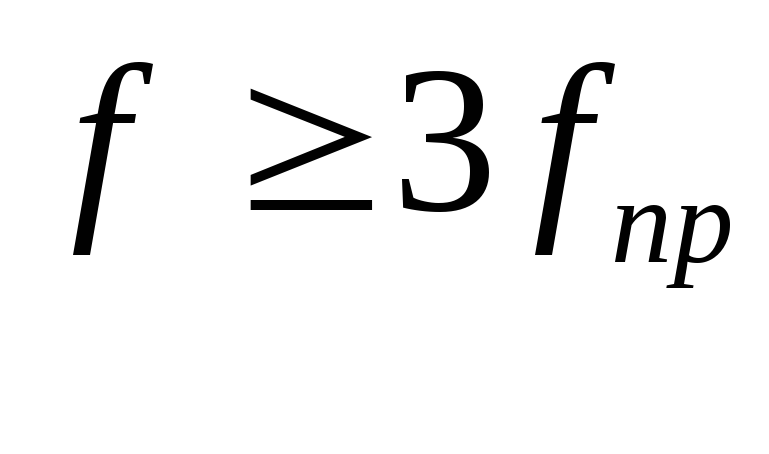где - наибольшая частота сигнала, пропускаемого непрерывной частью системы, Гц.

Расчет цифровых САУ следует вести так, чтобы выполнялись условия импульсной теоремы Котельникова – Шеннона:

«Для того чтобы передаваемая в виде импульсов информация могла быть воспроизведена без существенных искажений, наивысшая частота гармоник со значимыми амплитудами в спектре входного сигнала не должна превышать ½ частоты прерывания – частоты следования импульсов».

Разностные уравнения

Аналогом первой производной непрерывной функции для решетчатой функции является либо первая обратная разность

f[n] =f[n] -f[n-1],

либо первая прямая разность

f[n] =f[n+1] -f[n].

Прямая разность определяется в момент времениt=nTпо будущему значению решетчатой функции приt=(n+1)*Т. Это можно сделать в тех случаях, когда будущее значение известно.

Обратная разность определяется для момента времени t=nTпо прошлому значению решетчатой функции в момент времени (n- 1)*Т.

Аналогом второй производной служат вторые разности:

Обратная .

Для вычисления k-й разности используют рекуррентную формулу

или формулу общего вида

, (1)

где биномиальные коэффициенты (число сочетаний) .

Обратные разности обладают важной особенностью: если решетчатая функция определена только для положительных значений аргумента, то есть

при n<0, то в точкеn=0k-я разность

для любого целого положительного k.

Аналогами интегралов непрерывных функций в пределах от 0 до tдля решетчатых функций являются неполные суммы

и полные суммы

.

В качестве аналогов дифференциальных уравнений рассматриваются уравнения в конечных разностях.

При использовании обратных разностей уравнение в конечных разностях будет иметь вид

.

С учетом формулы (1) последнее выражение приобретает вид

,

коэффициенты уравнения определяются выражениями

, .

Общее решение однородного разностного уравнения при некратных корнях характеристического уравнения может быть записано следующим образом: , (2)

где (i=1,2,…,m) – корни характеристического уравнения

,

а - произвольные постоянные.

Из (2) вытекает условие того, чтобы свободное движение системы, описываемой разностным уравнением, было бы затухающим (условие устойчивости): ||<1 (i=1,2,…,m).

Для исследования решений разностных уравнений используются дискретное преобразование Лапласа, z– преобразование,w– преобразование, а также частотные методы.