Шпоры / шпоры тау / 2006 г. ЭВТд-ТАУ / 7-2006 г. Структ. сх. цифр.- Пример 2

8

Структурные схемы цифровых систем и их дискретные передаточные функции

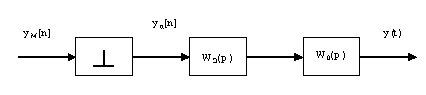
1. Последовательное соединение микроЭВМ с непрерывными динамическими звеньями.

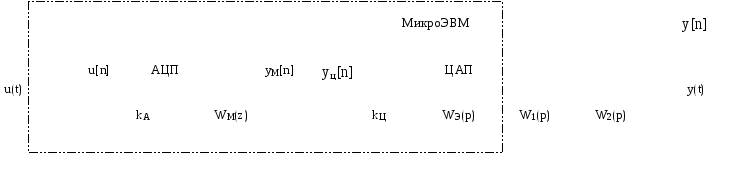
В форме преобразований Лапласа:

, обозначим , ,

применим z-преобразование, имея в виду, что

.

,

отсюда .

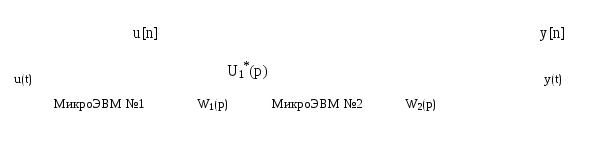Если система состоит из двух микроЭВМ, соединенных последовательно с непрерывными динамическими звеньями:

,

то ,

.

После z-преобразования

,

отсюда .

2. Система управления с отрицательной обратной связью.

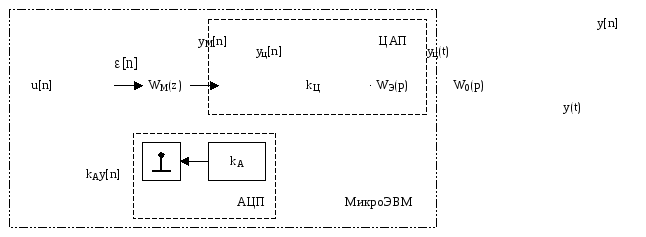
Базовая структурная схема цифровой САУ

САУ описывается следующей системой уравнений:

тогда

,

,

,

где - дискретная передаточная функция системы по сигналу рассогласования.

- в форме z - преобразований.

Так как ,

то ,

где - дискретная передаточная функция системы по каналу управления.

- дискретная передаточная функция системы с отрицательной обратной связью по каналу управления.

Определим дискретную передаточную функцию системы по каналу возмущения, воздействующего на объект:

ε₁(t)

;

;

тогда

Параметры входного воздействия входят в полученное выражение неявно.

Получить передаточную функцию не удается, так как входное воздействие выражено неявно.

Устойчивость работы цифровых САУ

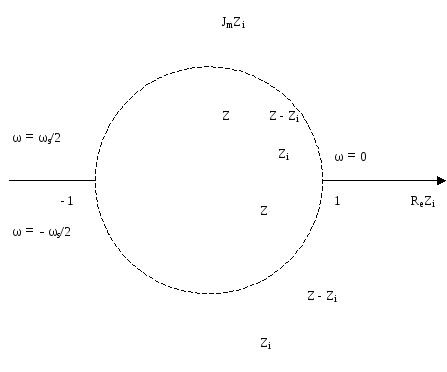Пусть известен многочлен знаменателя передаточной функции замкнутой цифровой САУ , где . , если расположен внутри круга единичного радиуса,

, если - вне круга, при изменении .

Будем рассматривать .

Комплексный спектр дискретной передаточной функции может быть назван также частотной передаточной функцией дискретной цепи.

1. Корневой метод анализа устойчивости.

Для того чтобы замкнутая цифровая система была устойчивой, необходимо и достаточно, чтобы модули корней характеристического уравнения замкнутой системы были меньше 1.

2. Критерий Михайлова.

Для того чтобы система была устойчива, необходимо и достаточно, чтобы при изменении ω от 0 до характеристический вектор имел приращение аргумента , где n – степень характеристического уравнения системы.

Кривая Михайлова должна поворачиваться на угол n.

3. Критерий Найквиста.

Так как при единичной отрицательной обратной связи, то , если .

В этом случае

при изменении ω от 0 до ,

где n - общее число корней;

m - число корней по модулю больше 1 в разомкнутой системе.

Для того чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы при изменении ω от 0 до вектор F(z) равный 1+W(z) имел приращение аргумента m, где m - число корней характеристического уравнения разомкнутой цифровой системы, лежащих вне круга единичного радиуса.

Пример 1. Пример 2.

Для того чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы при изменении ω от 0 до амплитудно-фазовая характеристика разомкнутой системы охватывала точку с координатами (-1,j0) m/2 раз против часовой стрелки, где m - число корней характеристического уравнения разомкнутой системы по модулю > 1.

4. Критерий Гурвица.

Формулировка критерия Гурвица для непрерывных систем справедлива и для дискретных систем, если в характеристическом уравнении системы произвести замену

w - преобразование.

Введем комплексную переменную w, связанную с комплексной переменной z билинейным преобразованием :

, где ;

.

При изменении частоты в пределах псевдочастота Ω пробегает все значения от - до +, а комплексная переменная w движется по оси мнимых чисел от -j до +j. Внутренняя часть круга единичного радиуса отображается при этом на левую полуплоскость.

При помощи w - преобразования осуществляется конформное отображение внутренности окружности единичного радиуса на плоскости z в левую полуплоскость w. При этом контур окружности единичного радиуса переходит в мнимую ось плоскости w.

ReZi

При исследовании дискретных систем по преобразованным при помощи w - преобразования передаточным функциям могут использоваться обычные приемы и критерии, справедливые для непрерывных систем, в том числе и

jω

JmZi

критерий Гурвица.

Логарифмические псевдочастотные характеристики

цифровых систем

Осуществим подстановку , ,

где - относительная безразмерная псевдочастота.

Введем понятие абсолютной псевдочастоты :

, с^-1;

.

При малых углах , тогда при выполнении условия можно в расчетах заменить псевдочастоту действительной круговой частотой, что может быть использовано, в частности, при расчетах реакции ЦАС на медленно меняющиеся гармонические сигналы на входе.

Пример 1. Пусть - интегратор; , .

.

Тогда .

Чтобы перейти к логарифмическим частотным характеристикам произведем подстановку : 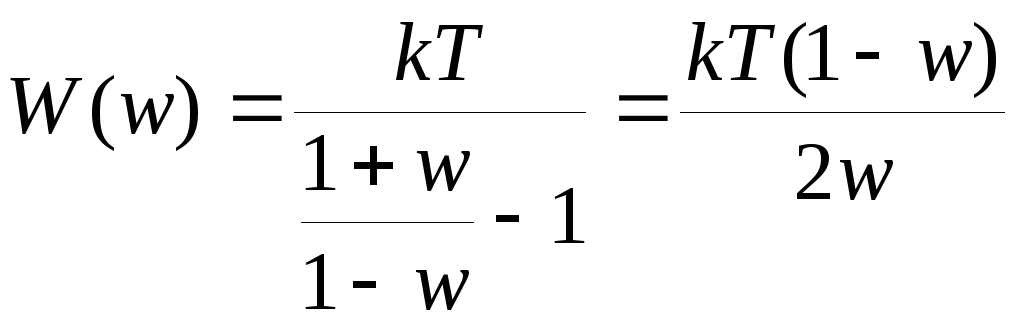, если вместо w подставить , получим псевдочастотную функцию : .

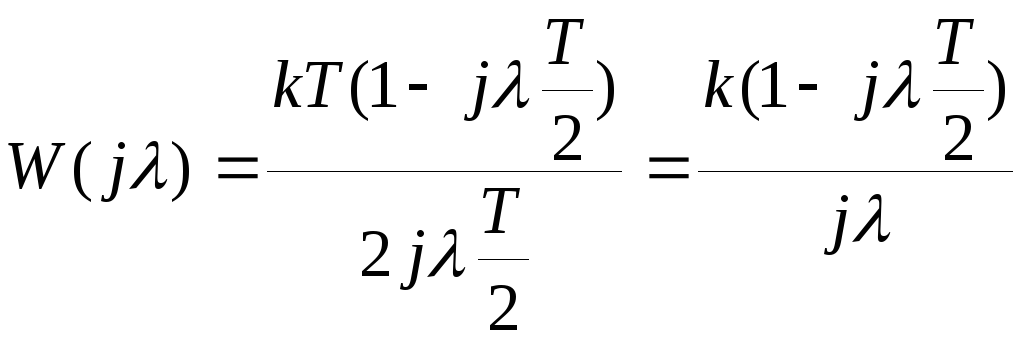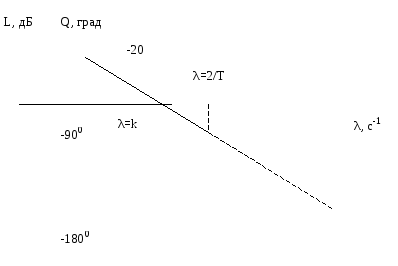- комплексный передаточный коэффициент интегрирующего звена с фиксатором 0-го порядка.

Свойства :

1. C уменьшением периода дискретизации (T0, =2/T ) характеристика приближается к характеристике непрерывной системы;

2. Предельный фазовый сдвиг равен -, такая замкнутая система приближается к границе устойчивости при больших k.

Пример 2.

Пусть , тогда

,

где .

.

Перейдем к псевдочастотным функциям :

,

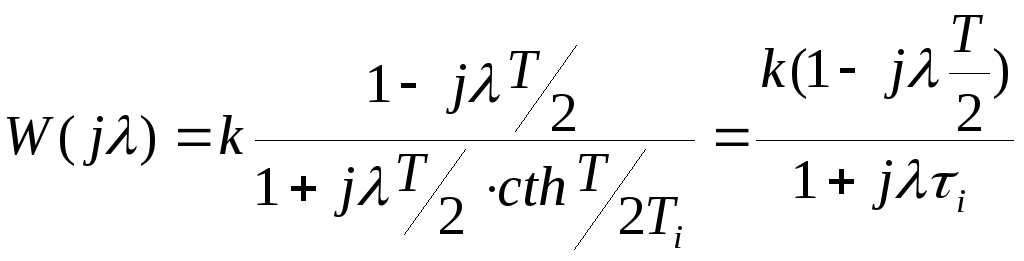так как 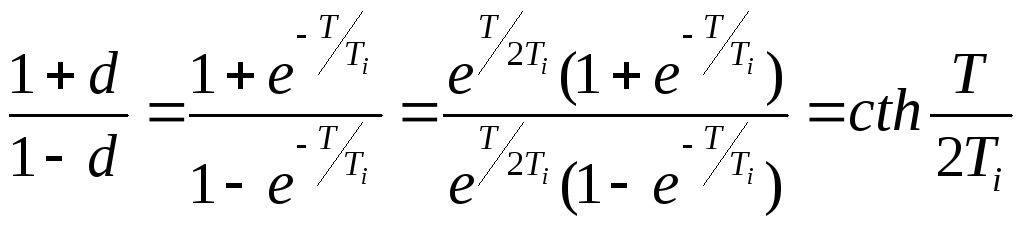. (1)

Исследуем это выражение :

1. Пусть период дискретности 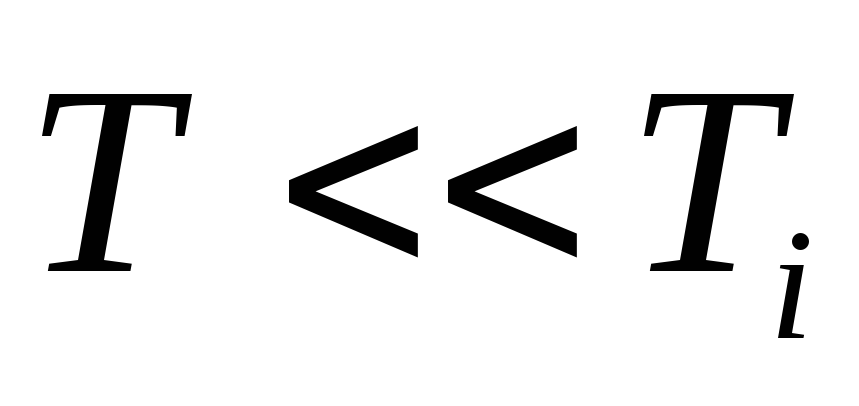[] и определим :

, это видно из выражения (1), отсюда , при этих соотношениях .
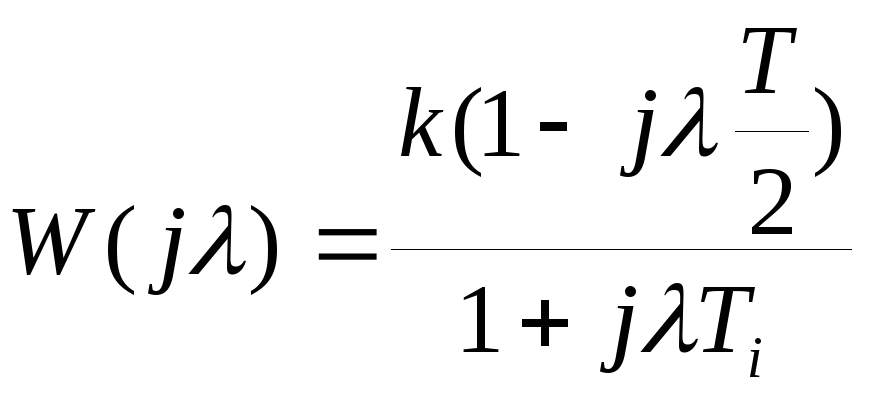