Шпоры / шпоры тау / 2006 г. ЭВТд-ТАУ / 9-2005г.CAУ с ЦВМ

5

Системы автоматического управления с ЦВМ

Литература:

1. Бесекерский В. А. Цифровые автоматические системы. М.: Наука, 1976.

2. Куо Б. Теория и проектирование цифровых систем управления. М.: Машиностроение, 1986.

3. Микропроцессорные системы автоматического управления. Под общ. ред. В. А. Бесекерского. Л.: Машиностроение, 1988.

4. Проектирование микропроцессорных систем автоматического управления. Ч. 1. Синтез системы автоматического управления: учеб. Пособие / Г. Г. Диркс, В. Г. Коломыцев; ПГТУ. Пермь, 1997.

5. Фёдоров С. М., Литвинов А. П. Автоматические системы с цифровыми управляющими машинами. М.-Л.: Энергия, 1965.

В многорежимных и многомерных САР, в системах с перестраиваемой структурой, многосвязных, высокоточных и многих других видах САУ получили широкое применение цифровые вычислительные машины.

МикроЭВМ выполняют функции задатчиков, сравнивающих устройств, устройств коррекции, автоматических регуляторов с быстроперестраиваемыми программами, коммутаторов, управляющих автоматов и других устройств.

Функциональная схема САУ с ЦВМ.

Применение микроЭВМ позволяет:

• Упростить САУ путём применения простых и надёжных модулей;

• Расположить цифровую вычислительную часть системы в непосредственной близости от основных элементов канала управления;

• Сложную обработку поступающей информации;

• Решения нескольких задач при обслуживании разных каналов управления с разделением по времени поступающей для обработки информации;

• Реализовать практически любой алгоритм управления;

• Осуществлять операции оптимизации САУ по статическим и динамическим показателям качества;

• Проводить операции контроля и поиска неисправностей.

Структурная типовая схема ЦАС

T- такт работы ЦВМ по преобразованию информации (0,01÷1с);

Wτ(p)= - передаточная функция ЦВМ, учитывающая временное запаздывание сигнала при прохождении по каналу АЦП-процессор-ЦАП; учитывается в ; τ<<T (τ=1мс);

Кацп – передаточный коэффициент АЦП;

Кцап- передаточный коэффициент ЦАП;

-(ИЭ1) идеальный импульсный элемент первого рода, который преобразует непрерывную

функцию в решетчатую

-(ИЭ2) ) идеальный импульсный элемент второго рода, преобразующий решетчатую функцию yм[n] в последовательность дельта-функции.

При проектировании цифровых САУ стремятся выбрать период Т так, чтобы он был намного меньше основной постоянной времени непрерывной части системы.

Период квантования Т можно определить с помощью приближенной формулы:

, где n-число двоичных разрядов,

-максимальная скорость изменения непрерывного сигнала.

Квантование по времени- важнейший признак класса цифровых систем, а квантование по уровню- нелинейных систем.

В приближенных расчетах шумами квантования по уровню и нелинейностями статистических характеристик АЦП и ЦАП пренебрегают.

Экстраполятор нулевого порядка

при =1 - передаточная функция

фиксирующего устройства нулевого порядка.

Математическое описание работы

модуляторов во временном пространстве

Аналого-цифровой модулятор. Вид модуляции: кодо-импульсная.

, где .

Условие допустимости сведения импульсной системы к непрерывной

,

где - наибольшая частота сигнала, пропускаемого непрерывной частью системы, Гц.

Расчет цифровых САУ следует вести так, чтобы выполнялись условия импульсной теоремы Котельникова – Шеннона:

«Для того чтобы передаваемая в виде импульсов информация могла быть воспроизведена без существенных искажений, наивысшая частота гармоник со значимыми амплитудами в спектре входного сигнала не должна превышать ½ частоты прерывания – частоты следования импульсов».

Аналогом первой производной непрерывной функции для решетчатой функции является либо первая обратная разность

f[n] = f[n] - f[n-1].

Аналогом второй производной служат вторые обратные разности:

.

Обычно разностные уравнения записывают в виде

,

решают уравнения применением дискретного преобразования Лапласа, z- или ω-преобразований.

Для решётчатых функций введено понятие дискретного преобразования Лапласа в соответствии с формулой

z-преобразование вытекает из дискретного преобразования Лапласа путем введения новой переменной :

Цифровой И-регулятор

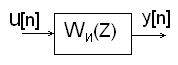Численное интегрирование функции u(t) при нулевых начальных

условиях по методу Эйлера:

,

отсюда -рекуррентное уравнение при интегрировании входного воздействия.

Применим дискретное преобразование Лапласа:

отсюда

Цифровой Д-регулятор

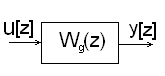
Численное дифференцирование функции u(t) при нулевых

начальных условиях методом простой разности

,отсюда

Цифровой ПИД-регулятор

Разностное уравнение регулятора:

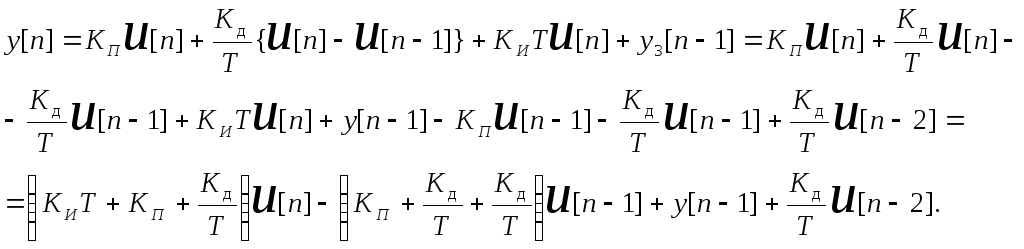
преобразование разностного уравнения имеет вид

отсюда

откуда

где Т-такт квантования сигналов.