П3.3. Параллельные алгоритмические системы

В теории параллельных алгоритмов дается конструктивное определение модели коллектива вычислителей. Пусть дано счетное множество универсальных машин Тьюринга с дополнительным набором операций коллективных взаимодействий (Т,К,Н,Q) и задана целочисленнаяn-мерная решеткаL,n=1,2,3. В решетке все узлы находятся на одинаковых расстояниях друг от друга по всем координатам (расстояние произвольное, но конечной длины). Узлы в решетке соединены ребрами, и в каждом узле помещена машина Тьюринга (рис.П3.4). Полученная решетчатая структураL_Мс размещенными в ее узлах машинами Тьюринга называется структурной схемой модели коллектива вычислителей.

Структурной схеме модели коллектива вычислителей ставится в соответствие решетчатый граф с переменной структурой G_V(рис.П3.5). Переменные вершиныVграфа G_Vпредставляют собой контуры с множествами изолированных полюсов р и матрицей К(t), с помощью которой задаются всевозможные коммутации на множестве полюсов р посредством звеньев - совокупности реберp_i-k_ij(t)-p_j, проведенных внутри контура:

К(t)=|k_ij(t)|, i,j=1,...m;

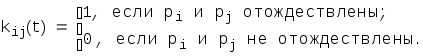
Меняя k_ij(t), можно задавать всевозможные отождествления между полюсами.

Пусть задана целочисленная решетка Gвn-мерном пространстве (n=1,2,3), узлами которой являются вершиныV, а ребрами - пучки звеньев, отождествляющих полюсы соседних вершин.

Решетка Gс множеством вершинVназывается решетчатым графом с переменной структуройG_V. Решетчатому графуG_Vставится в соответствие структурная схема модели коллективаL_M. Решетчатый графG_Vс выделенным множеством полюсов для машин Тьюринга называется структурной моделью коллектива вычислителейG_V-L_M. При функционировании моделиG_V-L_Mпредполагается, что работа всех машин Тьюринга осуществляется одновременно. За время одного шага в структурной модели символ, обозреваемый головкой одной из машин Тьюринга, может быть воспринять любой другой машиной в том же такте. Модель функционирует путем последовательного прохода ряда фаз: настройки (задается коммутацияK(t)для каждой из вершинVграфаG_V); обмена (задаются Т- или К-обмены); работы (независимое вычисление каждой машиной Тьюринга); управления (проверяется выполнение коллективного условного переходаQ) (рис.П3.6).

В теории параллельных алгоритмов установлены следующие важные свойства модели коллектива вычислителей:

модель в предложении неограниченного наращивания числа вычислителей (машин Тьюринга) является алгоритмически универсальной, структурно универсальной, универсальной при реализации параллельных алгоритмов;

производительность модели, пропорциональная производительности вычислителя и числу вычислителей, неограниченно растет при неограниченном росте числа вычислителей. Допускается наращивание производительности путем простого добавления вычислителей в модель;

модель является живучей, т.е. при выходе отдельных вычислителей сохраняется работоспособность модели при несколько сниженной производительности;

сложность вычислительных средств на основе данной модели не превышает существенно сложности вычислительных средств на основе модели вычислителя, если последняя реализует требуемую производительность.