
- •ЛЕКЦИЯ №3
- •ПОВЕРХНОСТИ
- •3.1. ПОВЕРХНОСТИ. кЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ
- •3.1.1. Кривые линии
- •3.1.2. Образование и задание поверхностей
- •3.1.3. Классификация поверхностей
- •3.1.4. Гранные поверхности и многогранники
- •3.1.5. Развертываемые линейчатые поверхности
- •3.1.6. Неразвертываемые линейчатые поверхности
- •3.3. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ПЛОСКОСТЯМИ ЧАСТНОГО ПОЛОЖЕНИЯ
- •3.3.1. Методы решения задач
- •3.3.2. Пересечение гранных поверхностей проецирующими плоскостями
- •3.3.3. Сечение криволинейных поверхностей проецирующими плоскостями
- •3.4. ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКОВ И КРИВЫХ ПОВЕРХНОСТЕЙ ПЛОСКОСТЬЮ ОБЩЕГО ПОЛОЖЕНИЯ
- •3.4.1. Сечение гранных поверхностей плоскостью общего положения
- •3.4.2. Сечение криволинейных поверхностей плоскостями общего положения
- •3.5. ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
- •3.5.1. Общие положения
- •3.5.2. Взаимное пересечение многогранников
- •3.5.3. Построение линии взаимного пересечения поверхностей с использованием в качестве посредников плоскостей частного положения.
- •3.5.4. Построение линии взаимного пересечения поверхностей с помощью метода сфер
- •3.5.5. Частные случаи взаимного пересечения поверхностей
- •3.6. Вопросы для самоконтроля
ЛЕКЦИЯ №3
ПОВЕРХНОСТИ План лекции:
3.1.Поверхности. Классификация поверхностей
3.2.Точки и линии на поверхности
3.3.Пересечение поверхностей плоскостями частного положения
3.4.Пересечение многогранников и кривых поверхностей плоскостью общего положения
3.5.Взаимное пересечение поверхностей
3.6.Вопросы для самоконтроля
3.1. ПОВЕРХНОСТИ. КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ
3.1.1. КРИВЫЕ ЛИНИИ
Кривую линию можно рассматривать как: а) траекторию движения точки;
б) линию пересечения поверхности плоскостью; в) линию пересечения поверхностей.
Кривые линии разделяются на плоские и пространственные. Все точки плоской кривой лежат в одной плоскости. Точки пространственной кривой не лежат в одной плоскости.
Порядок кривой определяется степенью уравнения, описывающего эту кривую. Геометрически порядок кривой определяется количеством точек «n» пересечения кривой с прямой линией (рис. 3.1).
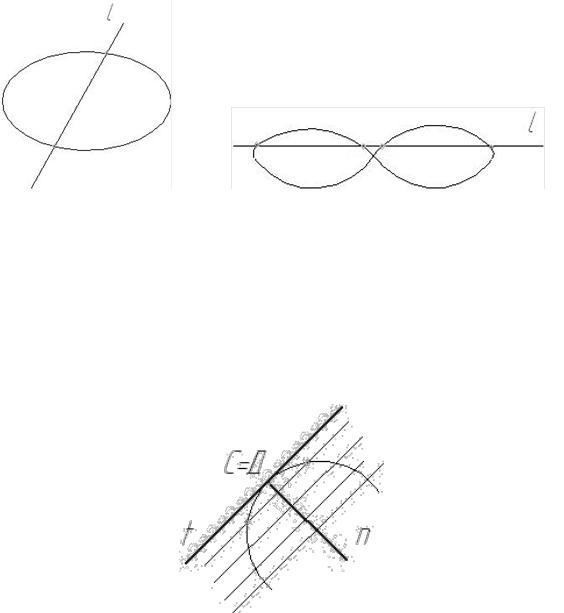
а) эллипс (n=2) |
б) лемниската Бернулли (n=4) |
|
Рис. 3.1. |
Прямая линия, |
соединяющая две бесконечно близкие |
(практически совпадающие) точки С=Д кривой называется касательной «t» (рис.3.2)
Рис. 3.2.
Прямая «n», проведенная в плоскости кривой перпендикулярно к касательной в точке касания называется нормалью.
Точка перегиба кривой – это точка М на рис. 3.3. в которой изменяется направление вращения касательной «t» (касательная переходит на другую сторону кривой).

Рис.3.3
Кплоским кривым линиям относятся окружность, эллипс, парабола, гипербола и другие.
Кпространственным кривым относятся цилиндрические и коническая винтовые линии, спираль Архимеда и ряд незакономерных кривых линий, которые не описываются уравнением.
Одной из широко распространенных в технических изделиях является цилиндрическая винтовая линия – это пространственная спиральная кривая, расположенная на поверхности кругового цилиндра и пересекающая все его образующие под одинаковым углом
(рис. 3.4).
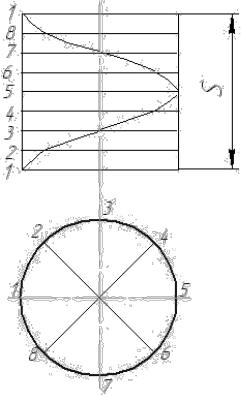
Рис. 3.4
Величина «S» перемещения точки винтовой линии в направлении оси, соответствующую одному полному обороту ее вокруг оси, называется шагом винтовой линии.
Для построения винтовой линии окружность ее горизонтальной проекции разделена на 8 равных частей. На такое же число равных частей делится и ее шаг «S». Через точки деления окружности проводят вертикальные линии связи. Через точки деления окружности проводят вертикальные линии связи. Через соответствующие точки деления шага проводят горизонтальные линии. Точки пересечения соответствующих линий определит фронтальную проекцию цилиндрической винтовой линии.
Более полные сведения о кривых линиях можно получить из лекции на эту же тему для самостоятельной работы студентов.
К началу лекции 3.1.2. ОБРАЗОВАНИЕ И ЗАДАНИЕ ПОВЕРХНОСТЕЙ
В начертательной геометрии поверхность рассматривается как геометрический образ, полученный движением некоторой линии в пространстве.
Способы задания поверхностей; а) аналитический; б) кинематический; в) каркасный.
При аналитическом способе поверхность задается уравнением. Способ образования поверхности непрерывным перемещением
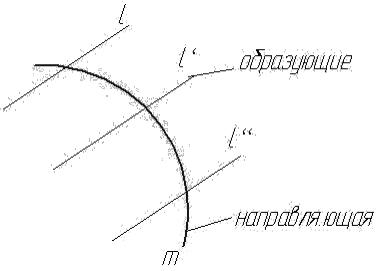
некоторой линии (образующей) по определенному закону называется кинематическим.
Закон перемещения образующей определяется линиями, называемыми направляющие (m) по которым скользит образующая «l». При своем движении (рис. 3.5) образующая остается параллельной самой себе (l || l’|| l” и т.д.)
Рис. 3.5
При каркасном способе задания поверхность рассматривается как совокупность достаточно плотной сети линий, определяющих поверхность. Эта сеть линий и называется каркасом (рис. 3.6).
