видимость прямых на П2. Очевидно, что координата точки «2», больше, чем «1», поэтому на П2 видима прямая АВ, на которой лежит точка «2».

При определении видимости на П1 очевидно, что координата «Z»

точки «4» больше, чем «3». Поэтому на П1 видима прямая АВ (4 AB).

План лекции

2.10. ПРОЕКЦИИ ПЛОСКИХ УГЛОВ

Если обе стороны любого угла параллельны плоскости проекций, то он проецируется на нее в натуральную величину.

Если хотя бы одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость прямой угол проецируется в натуральную величину (теорема о проецировании прямого угла).

Для доказательства теоремы воспользуемся геометрической моделью на рис. 2. 19.

Дано: АСВ = 90 0; [ВС] || П1

Для доказательства теоремы продлим отрезок АС до пересечения с плоскостью П1 (рис. 2.19) и получим горизонтальный след прямой Н1, одновременно принадлежащую прямой и ее проекции. Из свойств ортогонального проецирования следует, что [ВС] || [В1С1]. Если через точку Н1 проведем прямую Н1Д1 || С1В1, то она будет параллельна и СВ, а, следовательно, С1Н1Д=900 и

А1С1Д1=900, что и требовалось доказать.

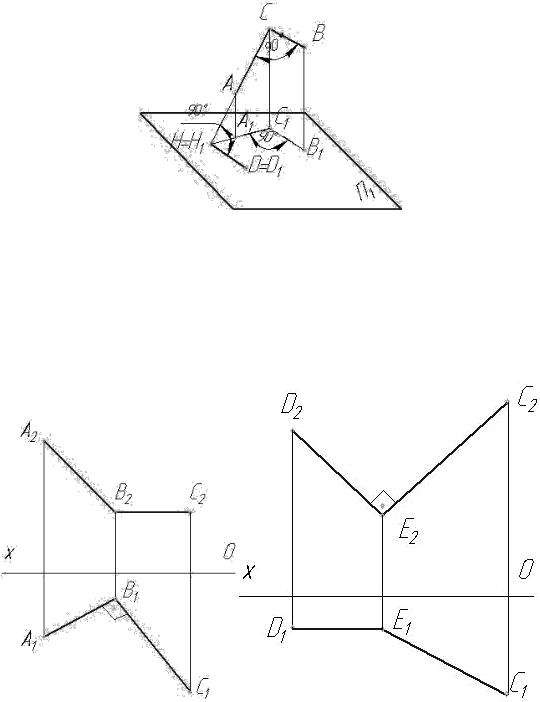
Рис. 2.19

На рис. 2.20 и 2.21 изображены прямые углы, одна из сторон которых параллельна одной из плоскостей проекций и проецирующиеся на них в натуральную величину.

2.11. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1.Перечислите названия прямых в зависимости от их положения по отношению к плоскостям проекций.

2.Какая прямая называется прямой общего положения?

3.Какие прямые называются профильными прямыми уровня?

4.Какие прямые называются проецирующими?

5.Что такое след прямой линии?

6.Сформулируйте правила построения следов прямой линии.

7.Назовите условие принадлежности точки прямой линии.

8.Определите длину отрезка и углы его наклона к плоскостям проекций методом прямоугольного треугольника.

9.Охарактеризуйте варианты взаимного положения двух

прямых.

10.Сформулируйте порядок определения видимости ребер гранных поверхностей методом конкурирующих точек.

11.Сформулируйте теорему о проецировании прямого угла.

План лекции