
- •Федеральное агентство по образованию
- •1.Краткие теоретические сведения
- •1.1.Микросостояние. Вероятность. Средние значения
- •1.2. Распределение Максвелла
- •1.3.Распределение молекул по модулям скорости
- •1.6. Распределение молекул по энергиям
- •2. Описание экспериментальной установки и методики измерений
- •3. Порядок выполнения работы
- •4. Требования к оформлению отчета
- •5. Контрольные вопросы
- •6.Список литературы
Федеральное агентство по образованию
ГОУ ВПО Рыбинская государственная авиационная
технологическая академия им. П. А. Соловьева
Кафедра Общей и технической физики
Лаборатория «Статистическая физика и термодинамика»
УТВЕРЖДЕНО
на заседании методического
семинара кафедры физики
« » _________ 2007 г.
Зав.каф. Пиралишвили Ш.А.
ЛАБОРАТОРНЫЕ РАБОТЫ
ПО СТАТИСТИЧЕСКОЙ ФИЗИКЕ И ТЕРМОДИНАМИКЕ
ЛАБОРАТОРНАЯ РАБОТА №CТ-1
Измерение функции распределения электронов
вольфрамового термокатода
Методическое руководство
разработано доц. Суворовой З.В.
Рецензент Шувалов В.В.
Рыбинск, 2007 г.
УКАЗАНИЯ ПО
ТЕХНИКЕ БЕЗОПАСНОСТИ
К работе с прибором допускаются лица, ознакомленные с устройством, принципом работы и прошедшие инструкцию по технике безопасности.
Запрещается включать установку в сеть без заземления.
Запрещается работать со снятым кожухом установок.
Прибор имеет подключение к электрической сети. Соблюдайте формы электробезопасности и требования инструкции №170 по технике безопасности. Не включайте прибор в сеть, пока не ознакомитесь с его конструкцией и основными требованиями к работе с ним.
Перед началом работы убедитесь, что тумблеры выключены, а переключатели находятся в крайнем левом положении.
Цель работы: исследование функции распределения термоэлектронов и определение параметров Максвелловского закона распределения.
1.Краткие теоретические сведения
1.1.Микросостояние. Вероятность. Средние значения
Для исследования
и количественного описания статистических
закономерностей в статистической физике
вводят многомерное пространство, которое
называется фазовым пространством. Это
такое пространство, в котором в качестве
координатных осей выбираются координаты
![]() и импульсыpi
частиц,
входящих в макроскопическую систему
А.
Если в систему входит N частиц, то
размерность фазового пространства
3N+3N=6N
(3N
координатных осей- проекции координат
всех частиц системы А,
3N
координатных осей- проекции импульсов).
и импульсыpi
частиц,
входящих в макроскопическую систему
А.
Если в систему входит N частиц, то
размерность фазового пространства
3N+3N=6N
(3N
координатных осей- проекции координат
всех частиц системы А,
3N
координатных осей- проекции импульсов).

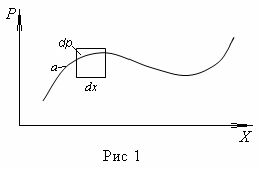 Если система
характеризуется одной степенью свободы,
то фазовое пространство двумерно (см.
рис.1). Точка а
фазового пространства характеризует
микросостояние системы А
(т.е. совокупность всех координат
Если система
характеризуется одной степенью свободы,
то фазовое пространство двумерно (см.
рис.1). Точка а
фазового пространства характеризует
микросостояние системы А
(т.е. совокупность всех координат
![]() и
импульсовpi
всех частиц
системы А)
в некоторый момент времени и называется
фазовой точкой.
и
импульсовpi
всех частиц
системы А)
в некоторый момент времени и называется
фазовой точкой.
Из-за взаимодействия частиц между собой и с окружающим пространством положение фазовой точки а в следующий момент времени изменится, т.е. фазовая точка сместится по фазовой траектории (кривая на рис.1).
Если через каждые
![]() измерять
измерять![]() иpi
частиц
системы А
и наносить точку в фазовом пространстве,
то спустя большие время Т
в фазовом
пространстве получается облако точек.
Эти точки изображают возможные
микросостояния системы А,
совместимые с данным макросостоянием.
За время Т
система А
побывает во всех возможных микросостояниях,
которые совместимы с данным макросостоянием.
иpi
частиц
системы А
и наносить точку в фазовом пространстве,
то спустя большие время Т
в фазовом
пространстве получается облако точек.
Эти точки изображают возможные
микросостояния системы А,
совместимые с данным макросостоянием.
За время Т
система А
побывает во всех возможных микросостояниях,
которые совместимы с данным макросостоянием.
Рассмотрим
некоторый объем dV
фазового пространства, соответствующий
значениям координат и импульсов частиц,
лежащих в интервале
![]() ,
,
![]()
Если dt
- время, в течение которого микросостояние
системы А
изображается фазовыми точками,
находящимися в объеме dV,
то величину
![]() можно рассматривать как частоту события
(точнее - как вероятность) того, что при
наблюдении за системойА
эта система в произвольный момент
времени находится в одном из микросостояний
с координатами x;
х+dx и импульсом
p; p+dp.
Ясно, что чем больше выбран объем dV,
тем больше вероятность застать в нем
фазовую точку, т.е.
можно рассматривать как частоту события
(точнее - как вероятность) того, что при
наблюдении за системойА
эта система в произвольный момент
времени находится в одном из микросостояний
с координатами x;
х+dx и импульсом
p; p+dp.
Ясно, что чем больше выбран объем dV,
тем больше вероятность застать в нем
фазовую точку, т.е.
![]() ,
,
где
![]() - функция статистического распределения.
- функция статистического распределения.
Рассмотрим
случай, когда случайная величина х
имеет непрерывный характер (например,
скорости молекул). Для этого разобьем
всю область изменения х
на отдельные
интервалы и будем считать число попаданий
случайной величины в тот или иной
интервал. Во избежание заметных флуктуаций
интервалы должны быть достаточно
большими, чтобы в каждом интервале
число попаданий было
![]() >>1
и чтобы можно было определить вероятность
попадания случайной величины в данный
интервал. Вместе с тем, интервалы должны
быть достаточно небольшими, чтобы более
детально характеризовать распределение
величиных.
>>1
и чтобы можно было определить вероятность
попадания случайной величины в данный
интервал. Вместе с тем, интервалы должны
быть достаточно небольшими, чтобы более
детально характеризовать распределение
величиных.
Итак, мы имеем
достаточно большое число достаточно
небольших интервалов. Допустим, нам
известна вероятность
![]() попадания
в тот или иной интервал ∆x.
Сама величина ∆
попадания
в тот или иной интервал ∆x.
Сама величина ∆![]() весьма мала, поэтому в качестве
характеристики случайной величины
берут отношение ∆
весьма мала, поэтому в качестве
характеристики случайной величины
берут отношение ∆![]() /∆x,
которое для достаточно малых ∆х
не зависит от величины самого интервала
∆x.
Это отношение
при ∆х
—>
0 называют функцией распределения
f(х)
случайной величины х:
/∆x,
которое для достаточно малых ∆х
не зависит от величины самого интервала
∆x.
Это отношение
при ∆х
—>
0 называют функцией распределения
f(х)
случайной величины х:
![]() .
(1)
.
(1)
 Видно,
что функции распределения f(х)
можно приписать смысл плотности
вероятности, т.е. вероятности интересующей
нас величины оказаться в единичном
интервале вблизи значения х.
Видно,
что функции распределения f(х)
можно приписать смысл плотности
вероятности, т.е. вероятности интересующей
нас величины оказаться в единичном
интервале вблизи значения х.
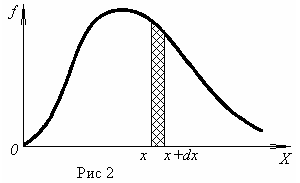
В разных
случаях функция распределения имеет
совершенно различный вид, один из
которых в качестве примера приведен
на рис. 2. В соответствии с (1) площадь
полоски шириной
dx
на этом
рисунке равна вероятности того, что
случайная величина х
окажется в пределах интервала (x,
x
+ dx):
![]() . Вероятность того, что величинах
попадает в интервал (a,b)
определяется выражением:
. Вероятность того, что величинах
попадает в интервал (a,b)
определяется выражением:![]() .
.
Ясно, что вероятность
того, что величина х
может принять хотя бы какое-нибудь
значение (достоверное событие), равна
единице. Это условие называют условием
нормировки:
![]() ,
где интегрирование производится по
всему интервалу возможных значений
величиных.
Из этого условия следует, что вся площадь
под кривой f(x)
равна единице (см. рис. 1).
,
где интегрирование производится по
всему интервалу возможных значений
величиных.
Из этого условия следует, что вся площадь
под кривой f(x)
равна единице (см. рис. 1).
Среднее значение величины x можно найти, зная ее нормированную на единицу функцию распределения f(x):
![]() ,
,
интегрирование
проводится по интересующему нас
интервалу значений х.
Аналогичные формулы справедливы для
любой функции φ(x),
например, для
![]() среднее значение определится так
среднее значение определится так
![]() .
.
