minimum_znaniy-1

1. Определенный интеграл

Пусть на некотором промежутке задана функция .

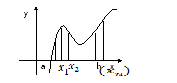
Произведём разбиение отрезка точками . Внутри каждого отрезка возьмём произвольную точку .

- интегральная сумма.

Устремим . Максимум - мелкость разбиения (характеристика разбиения).

Фигура под кривой называется криволинейной трапецией.

- определение определенного интеграла (если предел существует).

Геометрический смысл определенного интеграла - это площадь фигуры, ограниченной прямыми , осью и графиком функции .

2. Формула Ньютона-Лейбница. 

Если f(x) непрерывна на отрезке [a, b], и F(x) - некоторая первообразная функции , то .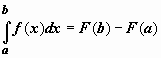 

3. Формула интегрирования по частям

Если u(x), v(x) - непрерывно дифференцируемые функции, то .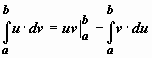 

Замена переменной в определённом интеграле. 

Пусть функция 

1. определена, непрерывно дифференцируема и монотонна на отрезке ,

2. ,

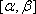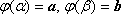3. функция 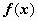 непрерывна на отрезке [a, b].

Тогда .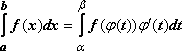

4. Признаки Деламбера и Коши сходимости рядов с неотрицательными членами.

Признак Даламбера:

Пусть дан знакоположительный числовой ряд

(7)

и пусть существует предел При p<1 ряд (7) сходится, при p>1 ряд (7) расходится.

Признак Коши:

Пусть дан знакоположительный числовой ряд u1+u2+…+un… (7)

и пусть существует предел При p<1 ряд (7) сходится, при p>1 ряд (7) расходится.

5. Степенной ряд. Теорема Абеля.

Важным случаем функциональных рядов являются степенные ряды:

(13)

или

Для выяснения свойств степенных рядов достаточно ограничиться рассмотрением рядов вида (13), так как ряд по степеням 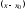легко свести к виду (13) заменой переменных 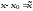, т.е. переносом начала координат в точку

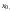
Для выяснения характера области сходимости степенного ряда сформулируем следующую теорему:

Теорема 6.1. (Абеля):

Пусть степенной ряд (13) сходится в точке 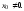Тогда он сходится абсолютно в любой точке х, для которой 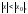и равномерно в любой области .

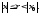Если степенной ряд (13) расходится в точке 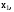то он расходится и во всех точках таких, что .

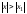Для определения области сходимости степенного ряда используется либо признак Даламбера, либо признак Коши.

6. Ряд Тейлора

Пусть функция f(x) имеет в точке х = а и некоторой ее окрестности производные порядка до (n+1) включительно.{ Т.е. и все предыдущие до порядка n функции и их производные непрерывны и дифференцируемы в этой окрестности}.

2) Пусть х- любое значение из этой окрестности, но а  х Тогда между точками х и а найдется такая точка , что справедлива формула: это выражение называется формулой Тейлора, а выражение: называется остаточным членом в форме Лагранжа.

7. Частные производные.

Пусть z=f(x,y). Зафиксируем какую-либо точку (x,y), а затем, не меняя закрепленного значения аргумента y, придадим аргументу x приращение . Тогда z получит приращение, которое называется частным приращением z по x и обозначается  и определяется формулой .

Аналогично, если x сохраняет постоянное значение, а y получает приращение , то z получает частное приращение z по y,.

Определение. Частной производной по x от функции z=f(x,y) называется предел отношения частного приращения по x к приращению при стремлении  к нулю, т.е.

Частная производная обозначается одним из символов.

Аналогично определяется частная производная по y:

                                 .

Таким образом, частные производные функции двух переменных вычисляются по тем же правилам, что и производные функции одного переменного.

8. Двойной интеграл. Сведение двойного интеграла к повторному.

Определение двойного интеграла. Пусть на плоскости XY задана функция 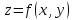и область (P) (область задания функции f(x,y)), её площадь P. Произведём разбиение площади сеткой кривых Pi, где Pi – частичная область. Внутри частичной области возьмём произвольную точку с координатами (ξi,ηi). Составим интегральную сумму: 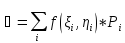. Пусть λ – характеристика разбиения, которая равна 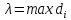, где di – диаметр частичной области. Диаметр – максимальное расстояние между любой парой точек в области. Устремим λ к нулю. Если существует предел интегральных сумм 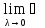, то этот предел и называется двойным интегралом: .

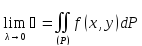Сведение к повторному:

Формула в общем виде: .

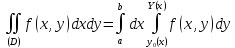9. Уравнения с разделяющимися переменными

Дифференциальное уравнение первого порядка y' = f(x,y) называется уравнением с разделяющимися переменными, если функцию f(x,y) можно представить в виде произведения двух функций, зависящих только от x и y:

где p(x) и h(y) − непрерывные функции.  Рассматривая производную y' как отношение дифференциалов , перенесем dx в правую часть и разделим уравнение на h(y):

Разумеется, нужно убедиться, что h(y) ≠ 0. Если найдется число x₀, при котором h(x₀) = 0, то это число будет также являться решением дифференциального уравнения. Деление на h(y) приводит к потере указанного решения.  Обозначив , запишем уравнение в форме:

Теперь переменные разделены и мы можем проинтегрировать дифференциальное уравнение:

где C − постоянная интегрирования.  Вычисляя интегралы, получаем выражение

описывающее общее решение уравнения с разделяющимися переменными

10. уравнение n-ого порядка с постоянными коэффициентами.

Дифференциальное уравнение вида

                                 (1)

где , f - известная функция, называется линейным дифференциальным уравнением n - го порядка с постоянными коэффициентами.

Если , то уравнение (1) называется однородным, в противном случае - неоднородным.