Minimum_po_integrallam

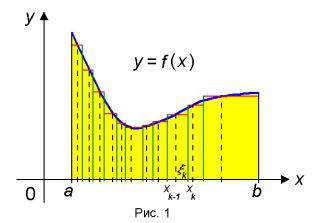
1. Определённый интеграл

Пусть на некотором промежутке x [a;b] задана функция y = f(x).

Произведём разбиение отрезка [a;b] точками x0 = a < x1 < x2 < ... < xk-1 < xk = b

Внутри каждого отрезка ∆xk = xk+1 — xk, (k = 1, ..., n) возьмём произвольную точку ξk и составим сумму:

n

σ = f(ξ1)∆x1 + f(ξ2)∆x2 + ... + f(ξn)∆xn = ∑ f (ξk )∆ xk

k=1

↑ интегральная сумма

Устремим n →∞, а max|∆xk| = λ →0 (Мелкость разбиений)

Отсюда выражаем определённый интеграл :

Геометрический смысл определённого интеграла - площадь фигуры, ограниченной прямыми x = a, x = b, осью ox и графиком функции f(x).

2. Формула Ньютона-Лейбница:

10. Степенной ряд:

Степенным рядом называется функциональный ряд вида:

∞

C0 +C1 (x−x0)+C2 (x−x0)2 +...+Cn (x−x0)n +...=∑ Cn( x−x0)n ,

n=0

Где Сn — не зависимая от x, но зависимая от n; X0 — конкретное число.

Радиус сходимости:

Радиус сходимости — такое число r, что ряд сходится при |x - x0| < R и расходится при |x - x0| > R. На границе радиуса сходимости ряд может как сходиться, так и расходиться.

Вычислить радиус сходимости можно по следующим формулам:

11. Дифференциал:

Если приращение функции ∆u = A1∆x1 + A2∆x2 + ... + Am∆xm + α1∆x1 + α1∆x1 + ... + α1∆x1 — называется приращением функции или дифференциалом.

Если проще, то дифференциал - произвольное бесконечно малое приращение переменной величины.

12. Градиент

Градиентом функции z = f(x,y) в точке M0(x0,y0) называется направленный отрезок grad z(M0) = zx'(M0)*i + zy'(M0)*j, отложенный

от точки M0, который показывает наискорейшее возрастание функции z = f(x,y) в данной точке.

Если проще, то градиент функции в точке M0 — это вектор, указывающий направление наибыстрейшего роста данной функции в точке M0.

13. Дифференциальные уравнения

Дифференциальное уравнение — уравнение, в которое входит неизвестная функция под знаком производной или

дифференциала.

Дифференциальное уравнение вида F(x, y, y', y'', ..., y(n)) = 0 называется дифференциальным уравнением n-ого порядка. Если проще, то порядком дифференциального уравнения называют максимальный порядок производной неизвестной

функции, входящей в дифференциальное уравнение.

Алгоритм и пример решения дифференциальных уравнений 1-ого порядка:

Общее решение дифференциального уравнения вида y' = f(x) на заданном интервале x можно отыскать, проинтегрировав обе части этого уравнения:

∫ y ' dy=∫f (x )dx

По свойствам определённого интеграла мы придём к искомому общему решению: y = F(x) + C, где F(x) — первообразная функции f(x) на промежутке x, а С — произвольная постоянная.

Если в условии не указывается промежуток x, то имеется ввиду что решение следует искать при всех x, входящих в ОДЗ.

При поиске частного решения уравнения y' = f(x), удовлетворяющее начальному условию y(x0) = y0, следует после нахождения

общего интервала вычислитьб значение постоянной С = С0, используя начальное условие, т.е. уравнение получит вид: y0 = F(x) + C0

Пример:

xy '= y

Далее смотрим, можно ли разделить переменные, т.е. в правой части оставить только x, а в левой только y

dyy =dxx

Далее интегрируем обе части уравнения:

Самым лучшим решением является решение вида y = y(x,C), поэтому пробуем привести наше уравнение к такому виду. Для этого нам достаточно произвольную постоянную следует занести под знак логарифма, т.е.

ln|y|=ln|x|+ln|C| , из свойств логарифма ln|y|=ln|Cx| , а отсюда получаем y=Cx

Ответ: y = Cx, где С = const.