Глава 1. Предварительный анализ данных
1.1. Описательные статистики
Если исследователь хочет обобщить и описать распределение одной переменной, а также выяснить, существует ли зависимость между двумя или более переменными, то он применяет методы описательной статистики.
Основными показателями описательной статистики являются: - среднее:
х = |
∑ |
хi |
; |
(1.1) |
n |
|
|||
|
|
|
|
- стандартная ошибка:
μx = sn ;
-медиана (Ме) – значение признака, приходящегося на середину ряда распределения;
-мода (Мо) – это значение признака, которое чаще всего встречается в выборке;
-выборочная дисперсия:
)2 |
1 |
|
∑(хi − х) |
2 |
|
|
|
S |
= |
|
|
|
; |
(1.2) |
|
n −1 |
|
||||||
- среднее квадратическое отклонение:
S) = |
|
1 |
∑(хi − х)2 ; |
(1.3) |
n |
−1 |
-эксцесс – характеристика островершинности статистического
распределения: для нормального распределения Ek =0, если Ek<0, то распределение будет более островершинным, чем нормальное; если Ek>0, то более плосковершинным:
|
μ |
4 |
|
n(n +1) |
n |
x |
i |
− x |
4 |
3(n −1) |
2 |
|
|||
Ek = |
|
−3 = |
|
∑ |
|
|
|
− |
|
|
|
, |
|||
σ |
4 |
(n −1)(n −2)(n −3) |
|
|
s |
(n − |
2)(n −3) |
||||||||
|
|
|
i=1 |
|
|
|
|
|
|||||||
где μ4 – выборочный центральный момент 4-го порядка;
-коэффициент асимметрии (skewness), для нормального распределения этот коэффициент равен нулю:
|
|
|
n |
n x |
i |
− x |
3 |
||
|
Аs |
= |
|
∑ |
|
|
|
; |
|
|
(n −1)(n −2) |
|
|
s |
|||||
- |
размах выборки: |
|
i=1 |
|
|
|
|||
|
R = xmax − xmin ; |
|
|
|
|
||||
|
|
|
|
|
|
|
|||
- |
максимальное значение выборки |
|
xmax ; |
||||||
- |
минимальное значение выборки |
xmin ; |
|
||||||
n
- сумма всех значение выборки ∑xi ;
i=1
- объем выборки n;
- наибольшее значение признака, имеющее разность с порядком xmax k единиц;
- наименьшее значение признака, имеющее разность с порядком xmin k единиц;
- уровень надежности (предельную ошибку выборки:
x = tα μx ,
где tα - значение распределения Стьюдента для уровня значимости
α и числа степеней свободы k=n-1.
Решим задачу в программе Excel с помощью пакета «Анализ данных». Для проведения процедуры описательной статистики на панели инструментов выберите «Сервис», затем «Надстройки» и при появлении окна поставить флажок на «Пакет анализа», нажать ОК. Для решения задачи
введем данные задачи в столбце А (рис.1.3).
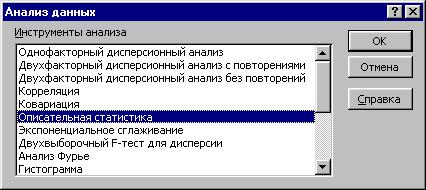
Выберите еще раз «Сервис» и «Анализ данных». При появлении окна «Анализ данных» - нажмите курсором на инструмент анализа: «Описательная статистика» (см. рис. 1.1).
Рис. 1.1. - Окно «Анализ данных»
Появится окно «Описательная статистика» (рис. 1.2).
Необходимо отметить Входной интервал курсором, поставить флажок
вГруппирование – по столбцам и отметить флажком Итоговая статистика.
Врезультате появится рис. 1.3.
Рис. 1.2 - Окно «Описательная статистика»
Рис. 1.3 - Результаты решения задачи
1.2. Анализ зависимостимежду переменными
Установление и анализ взаимосвязей между переменными является основной частью эконометрического анализа данных.
Для оценки силы линейной зависимости между двумя переменными X и Y исчисляют ковариацию:
n
∑(xi − x)(yi − y)
cov(x, y) = |
i=1 |
|
, |
(1.4) |
|
n |
|||
|
|
|
|
где выборочные средние (1.1)
х = ∑nхi ; у = ∑nуi .
Ковариация имеет размерность, равную произведению размерностей случайных величин. Если ковариация положительна, то связь между переменными прямая, то есть с увеличением одного признака, второй также увеличивается, если ковариация отрицательная, то связь между X и Y обратная. Если ковариация равна нулю, то данные не связаны.
Если рассматриваем многомерную выборку, то возможно получить ковариационную матрицу:
|
2 |
cov(1,2) |
|
s1 |
|
cov(2,1) |
s22 |
|
сov(i, j) = |
|
... |
... |
||
|
|
cov(n,2) |
cov(n,1) |
||
... cov(1,n)
... cov(2,n)
... ... .
... sn2
Ковариационная матрица симметрична относительно главной диагонали. На главной диагонали матрицы стоят дисперсии (1.2).
Являясь мерой линейной зависимости между переменными, ковариация не позволяет оценить ее относительную силу.
Относительная сила связи между переменными, образующими двумерную выборку, измеряется выборочным коэффициентом корреляции:
rxy |
= |
cov(x, y) |
, |
(1.5) |
|
||||
|
|
sx sy |
|
|
где Sx и Sy – среднее квадратическое отклонение (1.3).
Коэффициент корреляции изменяется от –1 до +1. Аналогично ковариации, если коэффициент положителен, то связь между признаками прямая, если отрицателен, то обратная. Если rxy по абсолютной величине близок к нулю, то говорят об отсутствии связи, если близок к единице – то тесной.
Для многомерной выборки рассчитывается корреляционная матрица:
1 |
r |
... |
r |
|
|
|
12 |
|
1n |
|
|
r21 |
1 |
... |
r2n |
, |
|
r(i, j) = |
... |
... |
... |
|
|
... |
|
|
|||
r |
r |
... |
1 |
|
|
n1 |
n2 |
|
|
|
|
которая симметрична главной диагонали, на которой стоят единицы. Иногда, для анализа связи между переменными достаточно построить
поле корреляции или точечную диаграмму.
Задача 1
На основании данных об издержках обращения и изменения товарооборота, приведенных в таблице:
Издержки обращения, тыс. |
1,1 |
1,3 |
1,4 |
1,1 |
1,9 |
1,7 |
1,4 |
1,2 |
1,9 |
1,9 |
руб. (у) |
|
|
|
|
|
|
|
|
|
|
Товарооборот, тыс. руб. (x) |
4 |
5 |
6 |
3 |
8 |
9 |
6 |
4 |
6 |
9 |
Вычислите выборочные коэффициенты ковариации и корреляции.
Решение
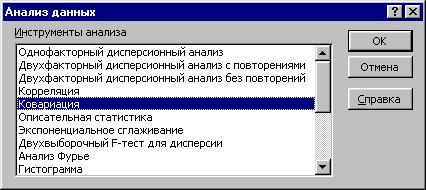
Введите данные таблицы по столбцам, затем выберите Сервис→Анализ данных→Ковариация (рис. 1.4).
Рис. 1.4 - Окно «Анализ данных»
При появлении окна «Ковариация» отметьте курсором Входной интервал – два столбца X и Y , Группирование – по столбцам, Параметры выхода – любую ячейку. В этой ячейке выведется результат (рис. 1.5).
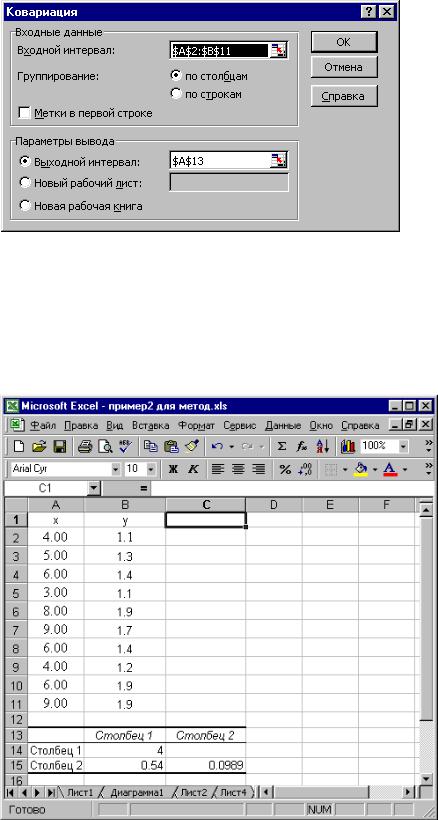
Рис. 1.5 - Окно «Ковариация»
Из анализа таблицы ковариационного анализа (рис.1.6) видно, что связь между товарооборотом Х и издержками обращения Y прямая (коэффициент ковариации равен 0,54). На главной диагонали стоят дисперсии признаков:
дисперсия s2х=4; s2у=0,0989.
Рис. 1.6 – Расчет задачи с помощью инструмента «Ковариация»
Аналогично проведем корреляционный анализ. Для этого:
1.Сервис→Анализ данных→Корреляция→ОК;
2.Входной интервал определяется курсором (буквы х и у не обводить);
3.Выходной интервал: любая ячейка, в которой появится результат.
4. ОК.
Результаты представлены на рис. 1.7.
Рис. 1.7 – Расчет задачи с помощью инструмента «Корреляция»
Как видно из рис. 1.7 коэффициент корреляции между переменными Х и Y равен 0,8585. Это означает, что между товарооборотом Х и издержками обращения Y наблюдается тесная положительная связь.
Построение точечной диаграммы проводится в продолжение этого примера в регрессионном анализе (парная регрессия).