
Ohrimenko+ / Barnsley. Superfractals
.pdf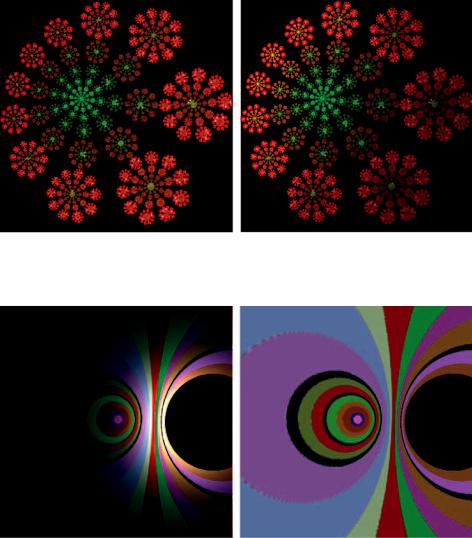
120 |
Transformations of points, sets, pictures and measures |
Figure 2.18 A picture (left) and a picture of a measure (right) both of which are invariant under the Mobius¨ rotation defined in Equation (2.3.4). Mobius¨ transformations are discussed in Section 2.6.
Figure 2.19 These pictures illustrate an invariant picture (right) and a closely related invariant measure (left) for the same Mobius¨ transformation as that discussed in Figure 2.6. See also Figure 2.20.
T h e o r e m 2.4.8 Let fn : H(X) → H(X) be a contractive transformation on (H(X), dH ) with contractivity factor ln , for n = 1, 2, . . . , N for some finite positive integer N . Then F : H(X) → H(X) defined by
F(B) = f1(B) f2(B) · · · fN (B) for all B H(X)
is a contractive transformation with contractivity factor l = max{ln : n =
1, 2, . . . , N }.

2.4 Fixed points and fractals |
121 |
Figure 2.20 This pair of pictures illustrates part of an invariant picture, on the left, and a closely related invariant measure, on the right, for the Mobius¨ transformation in Equation (2.2.1). See also Figures 2.6 and 2.19.
P r o o f We prove the result for the case N = 2. By Theorem 1.12.15,
dH (A1 A2, A3 A4) ≤ max{dH (A1, A3), dH (A2 A4)}
for all A1, A2, A3, A4 H(X). It follows that
dH ( f1(A) f2(A), f1(B) f2(B)) ≤ max{dH ( f1(A), f1(B)), dH ( f2(A), f2(B))}
|
≤ max{l1, l2}dH (A, B) |
for all A, B H(X). |
|
Notice that a contractive transformation fn : H(X) → H(X) need not derive from a contractive transformation fn : X → X. For example we may define f1 : H(X) → H(X) by
f1(B) = B0 for all B H(X)
for some fixed B0 H(X); then f1 : H(X) → H(X) is contractive but does not correspond to any transformation on X unless B0 = {b} for some b X.
D e f i n i t i o n 2.4.9 Let X be a complete metric space, and let the transformations fn : X → X be contractions. Then the unique fixed point of F : H(X) → H(X) is called the set attractor, or fractal set, associated with {X; f1, f2, . . . , fN }.
We will develop the theory in later chapters. We will refer to {X; f1, f2, . . . , fN } as an iterated function system or IFS. These terms were first introduced in [4]. We will say that ‘an IFS is contractive’ if the functions f1, f2, . . . , fN are contractions.

122 |
Transformations of points, sets, pictures and measures |
Figure 2.21 This figure shows a sequence of sets A 0, A 1, A 2, A 3, A 4, A 5 R2 obtained by successive application of the transformation F : H( ) → H( ). Here A 0 is a set that looks like an elephant and A n = F ( A n−1) = f1( A n−1) f2( A n−1) for n = 1, 2, 3, 4, 5 where f1, f2 are contractive with contractivity factor 0.5. The sequence of sets is converging towards the unique fixed point of F , in this case a straight line segment.
Figure 2.21 illustrates a sequence of sets in H( ) produced by successive application of the operator F in the case where N = 2 and f1 and f2 are contractive transformations that shrink by a linear factor 2.
Figure 2.22 shows an example of a fractal set, or set attractor, that is the fixed point of a transformation F : H(X) → H(X) constructed using two contractive transformations on R2.
E x e r c i s e 2.4.10 Consider the case where X |
= |
R, f (x) |
= |
2 |
+ |
1 x and g(x) |
= |
1 |
|
3 |
3 |
||||
3 x. Describe the unique fixed point of F : H(R) → H(R) in this case. |
|
||||||
The metric spaces (P(X), dP ) and (P(X), dP )
If your understanding of measures is new and frail you might wish to skip forward to Section 2.5 after briefly surveying the rest of the material in Section 2.4.
Here we define two metrics on P(X), dP = dP(X) and dP = dP(X). The resulting metric spaces (P(X), dP ) and (P(X), dP ) are complete. Furthermore, both metrics

2.4 Fixed points and fractals |
123 |
Figure 2.22 This picture represents, in red and mauve, the unique fixed point of a transformation F : H(R2) → H(R2) promised by Theorem 2.4.8. Here F( A ) := f1( A ) f2( A ) for all A H(R2), where f1, f2 : R2 → R2 are strictly contractive. Can you see how the fixed point is made of two transformations
of itself ?
are such that if f : X → X is a contraction mapping then f : P(X) → P(X) is a contraction mapping with respect to both the metrics dP and dP . That is, in both cases contractivity is inherited. So an analogous situation regarding the construction of contractive transformations and the existence of fixed points in (H(X), dH ), discussed above, applies both to (P(X), dP ) and to (P(X), dP ). This relates to the construction of fractal measures; this topic is developed in later chapters, particularly Chapter 4.
We begin by establishing the space (P(X), dP ) . The metric dP is quite easy to
understand on the basis of what has been |
encountered so far in this book. |
|
|
||||||||||
|
|
|
|
|
|
||||||||
T h e o r e m 2.4.11 Let (X, d) be a compact metric space. Let dP : P(X) |
× |
||||||||||||
P(X ) → [0, ∞) be defined by |
|
|
|
|
|
|
|
|
|||||
P (μ, ν) |
|
inf r |
0 : μ(A) |
|
ν( |
|
(r)) for all A |
B |
(X) |
|
P(X). |
||
d |
= |
{ ≥ |
|
≤ |
|
BA |
|
|
|
} for all μ,ν (2.4.2) |
|||
Then dP is a metric on P(X) and the metric space (P(X), dP ) is complete.
124 |
Transformations of points, sets, pictures and measures |
P r o o f |
Recall that BA(r) denotes the dilation of the set A by r ≥ 0, whereas |
B(X) denotes the Borel subsets of X. It is straightforward to show that dP is a based on
metric, and we leave this as an exercise. Completeness is proved in [9] |
|
[35], Theorem 9.1. See also [81], p. 160, and references given therein. |
|
D e f i n i t i o n 2.4.12 Let (X, d) be a compact metric space. The metric dP |
|
is called the uniform Prokhorov metric on P(X). |
|
This metric was introduced to fractal geometry by Falconer [34], because of its scaling property. John Hutchinson pointed it out to me and suggested the name. It is important to note that although (P(X), dP ) inherits from (X, d) the property of completeness, provided that the former space is compact, it does not in general inherit the property of compactness. For example, an infinite sequence of points in (P([0, 1]), dP ) is
|
n − 1 |
δ |
|
1 |
λ |
[0,1] |
∞ |
, |
|
n |
0 + n |
n=1 |
|||||||
|
|
|
|||||||
|
|
|
|
|
|
|
|
||
but the Prokhorov distance between each pair of distinct points in this sequence is unity, so this sequence contains no subsequence that is a Cauchy sequence. Here λ[0,1] denotes the uniform Borel measure of total mass unity on the real interval [0, 1].
E x e r c i s e 2.4.13 Show that dP (μ, ν) = 1 where μ is the uniform distribution of unit total mass on [0, 1] × [0, 1] R2 and ν = δ(1,1) is a unit mass located at the point (1, 1) R2.
E x e r c i s e 2.4.14 Verify that dP (μ, ν) = dP (ν, μ). Hint: Look at what happens when you replace a set by its complement in Equation (2.4.2).
Next we describe the metric space (P(X), dP ). The metric dP has the spectacular advantage over dP that it admits the inheritance of compactness. It has the disadinvolves measure-theoretic integration, which we do not develop in
vantage that it
this book; see [9] for a gentle formal presentation. Also, it is weaker than dP . This
latter weakness is also a strength, because d |
P |
provides contractivity in |
situations |
|||||||||||
|
|
|||||||||||||
where dP does not. |
|
|
|
|
|
|
|
|
|
|||||
|
The |
|
|
|
|
|
|
|
|
X |
hdμ, where |
|||
|
|
|
metric dP depends on the evaluation of integrals such as |
|
||||||||||
|
P |
X |
) and h : |
X |
→ |
R |
is continuous. Here you will not go far |
off course if your |
||||||
μ |
|
( |
|
|
|
|
|
|
|
|
||||
intuition is guided by the following fact: if the Borel measure μ is defined by a
continuous density function ρ : X → R, that is, μ(B) = B ρ(x)d x for all Borel
|
|
sets B, then X hdμ = |
X h(x)ρ(x)d x. |
2.4 Fixed points and fractals |
125 |
T h e o r e m 2.4.15 Let (X, d) be a compact metric space. Let dP : P(X) × P(X) → [0, ∞) be defined by
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dP |
(μ, ν) = |
sup |
X hdμ − X hdν : h Li p1( |
X |
) |
for all μ,ν |
P |
X |
). |
|||||
|
h: |
X |
→ |
R |
|
( |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
(2.4.3) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Then dP is a metric on P(X) and the metric space (P(X), dP ) is compact. |
|
|
||||||||||||
P r o o f |
It is straightforward to verify that dP is a metric. You might also |
|||||||||||||
be able to verify that the natural topology corresponding to the metric dP is exactly the same as what is called the weak* (‘weak-star’) topology on P(X), where a basis for the weak* topology is the set of ‘balls’ of measures Ball(a, b, h) :=
{μ P(X) : a < |
X hdμ < b} for all a < b R and all continuous h : X → R. |
||
By Alaoglu’s |
theorem, [30], p. 424, the weak* topology on P(X) is compact when |
||
|
|
|
|
X is compact, so (P(X), dP ) is a compact metric space. |
|
||
D e f i n i t i o n 2.4.16 Let (X, d) be a compact metric space. The metric dP defined in Equation (2.4.3) is called the Monge–Kantorovitch metric on P(X).
E x e r c i s e 2.4.17 Show that dP (μ, ν) = 12 when μ is the uniform distribution of unit total mass on [0, 1] × [0, 1] R2 and ν = δ(1,1) is a unit mass located at the point (1, 1) R2.
The following theorem tells us that the metric dP is stronger than dP . What it does not tell us is that it is almost too strong.
T h e o r e m 2.4.18 Let (X, d) be a compact metric space. Then
dP (μ, v) ≤ dP (μ, v) for all μ, v P(X).
P r o o f This is proved in [19]. You might like to try to prove it for yourself.
Contractive transformations on (P(X), dP ) and (P(X), dP ) and the existence of fractal measures
Throughout this section we assume that (X, d) is a compact metric space. When dealing with contraction mappings acting on an underlying space such as R2, we leave it up to you, gentle reader, to remember to work in a big closed ball of the space such that the transformations map this ball into itself.
We have previously shown that if a transformation f has the property of being contractive on a compact metric space X then this property is inherited when f acts on H(X). We have promised that this has spectacular consequences, which we shall see in Chapter 4. In this section we show that the same sort of infectious inheritance applies with regard to the action of f on P(X). This will lead us, in Chapter 4,
126 Transformations of points, sets, pictures and measures
to a constructive theory for those visually elusive beautiful mathematical objects, ‘deterministic’ fractal measures.
The following theorem tells us that the property of f of being a contraction
mapping is indeed inherited from (X, d) to (P(X), dP ) and to (P(X), dP ). |
|
|
|||
T h e o r e m 2.4.19 Let ( |
X |
metric space. Let |
f : X |
→ |
X |
|
, d) be a compact |
|
|
||
be a contractive transformation with contractivity factor l ≥ 0. Then f |
: P(X) → |
||||
P(X) is a contractive transformation with contractivity factor l, with respect to both the metrics dP and dP .
P r o o f For all μ, ν P(X) we have, assuming l > 0 for brevity,
dP ( f (μ), f (ν)) = inf r ≥ 0 : μ( f −1(A)) ≤ ν( f −1(BA(r ))) for all A B(X)
≤inf r ≥ 0 : μ( f −1(A)) ≤ ν(Bf −1(A)(r/ l))) for all A B(X)
≤l inf r ≥ 0 : μ(A) ≤ ν(BA(r)) for all A = f −1(A), A B(X)
|
|
|
|
|
|
≤ l inf r ≥ 0 : μ(A) ≤ ν(BA(r )) for all A |
B(X) |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
= ldP (μ, ν), |
|
|
|
|
− |
1 |
( |
|
|
|
(r)) |
|
|
|
|
|
(r/ l). |
|
|
|
|
||||||||||||||||
where we have used the observation that f |
|
|
A |
|
|
|
|
1 |
(A) |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Also, we have |
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
B |
f − |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
P |
|
|
|
|
|
|
|
|
sup |
|
|
|
|
|
|
◦ μ) − X hd( f ◦ |
ν) : h Li p1( |
X |
) |
||||||||||||||||||||||||
d |
( f (μ), f (ν)) = h:X→R X hd( f |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
sup |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
) |
|
|
|||
|
|
|
|
|
|
|
= h:X→R X h ◦ f dμ − X h ◦ f dν : h Li p1( |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
= |
l sup |
|
|
|
1 |
h |
|
f dμ |
|
|
|
1 |
|
h |
|
f dν : h |
|
|
Li p |
(X) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
◦ |
− l |
◦ |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
h:X |
→ |
R |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
(X) |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
sup |
|
|
|
|
|
− |
X hdν : |
h Li p1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
≤ lh:X |
→ |
R X hdμ |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
= |
l dP (μ, ν), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
where we have used the observation that |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
1 |
h |
◦ |
f (x) |
|
1 |
h |
◦ |
f (y) |
|
h(x) |
− |
h(y) |
| ≤ |
d(x, y) |
|
when h |
|
Li p1(X); |
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
l |
|
|
|
− l |
|
|
≤ | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
see also Hutchinson [48]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
E x e r c i s e 2.4.20 Let f (x) = 23 + 13 x as in Exercises 2.4.14 and 2.4.17 above. Then f is a contractive transformation on both (P(X), dP ) and (P(X), dP ) with contractivity factor 13 . Its unique fixed point is δ1, the measure that assigns unit mass to the point x = 1. Also, if μ0 P(X) and μn = f (μn−1) for n = 1, 2, 3, . . .
then we must have limn→∞ μn = δ1. For example, the sequence of measures
2λ[0, 12 ], 6λ[ 23 , 56 ], 18λ[ 89 , 1718 ], . . .
converges in both metrics, dP and dP , to δ1.

2.4 Fixed points and fractals |
127 |
It is clear that if f : X → X is a contractive transformation on a compact metric space X with unique fixed point a X then f : P(X) → P(X) is a contractive transformation on the complete metric space P(X) with unique fixed point δa . It might again appear, as in the case where f : H(X) → H(X), that we have not gained much with all our elaboration and inheritance. But we have: the construction that follows is the starting point for the theory of deterministic fractal measures.
Given that we have a set of continuous transformations { fn : P(X) → P(X) : n = 1, 2, . . . , N } and a set of probabilities p1, p2, . . . , pN > 0, with p1 + p2 +
· · · + pN = 1, we can define a new transformation F : P(X) → P(X), where
F(μ) = p1 f1(μ) + p2 f2(μ) + · · · + pN fN (μ) for all μ P(X). (2.4.4)
Notice that the transformations fn : P(X) → P(X) in this theorem need not derive from transformations fn : X → X. For example, we may define f1 : P(X) → P(X) by
f1(μ) = ω for all μ P(X),
for some fixed ω P(X).
T h e o r e m 2.4.21 Let fn : P(X) → P(X) be a Lipschitz transformation on (P(X), dP ), with Lipschitz constant ln for n = 1, 2, . . . , N , for some finite positive integer N . Then the transformation F : P(X) → P(X) defined in Equation (2.4.4) is Lipschitz with respect to dP , with Lipschitz constant
l = max{l1, l2, . . . , lN },
and Lipschitz with respect to dP with Lipschitz constant
l = p1l1 + p2l2 + · · · + pN lN .
In particular, F : (P(X), dP ) → (P(X), dP ) is a contraction mapping when l < 1 and F : (P(X), dP ) → (P(X), dP ) is a contraction mapping when l < 1.
P r o o f We prove the result for N = 2. We have, for all μ, ν P(X), that
dP (F(μ), F(ν))
= inf r ≥ 0 : F(μ)(A) ≤ F(ν)(BA(r )) for all A B(X)
= inf r ≥ 0 : p1 f1(μ)(A)+ p2 f2(μ)(A) ≤ p1 f1(ν)(BA(r)) + p2 f2(ν)(BA(r ))
for all A B(X)
≤ inf r ≥ 0 : p1 f1(μ)(A) ≤ p1 f1(ν)(BA(r)) and p2 f2(μ)(A) ≤ p2 f2(ν)(BA(r ))
for all A B(X)
≤ max{l1, l2} dP (μ, ν).
128 |
Transformations of points, sets, pictures and measures |
||||||||||||||||||
Also, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dP (F(μ), F(ν)) |
|
(μ) |
|
|
|
|
|
|
(ν) : h |
|
|
|
|
(X) |
|||||
|
sup |
|
hd |
F |
− X |
hd |
F |
|
Li p |
||||||||||
|
= h:X→R X |
|
|
|
|
|
|
|
1 |
|
|
||||||||
|
sup |
X hd f1 |
(μ) − X hd f1(ν) + p2 X hd f2(μ) − X hd f2(ν) : |
||||||||||||||||
|
= h:X→R p1 |
||||||||||||||||||
|
sup |
|
|
p |
1 X |
h |
d f |
(μ) |
− X |
h |
d f |
(ν) |
h Li p1(X) |
||||||
|
≤ hi :X→R,i {1,2} |
1 |
|
1 |
|
|
|
1 |
|
1 |
|
|
|
||||||
+ p2 X h2d f2(μ) − X h2d f2(ν) : h1, h2 Li p1(X)
=p1dP ( f1(μ), f1(ν)) + p2dP ( f2(μ), f2(ν))
≤( p1l1 + p2l2)dP (μ, ν).
Generally speaking we call the fixed points of the transformation F : P(X) → P(X) fractal measures or measure attractors.
An example of a sequence of measures μ0, μ1, μ2, μ3, μ4, μ5 P( ) converging towards a fixed point μ∞ P( ) is shown in Figure 2.23; μ0 is represented by a green rectangle and μn = F(μn−1) for n = 1, 2, 3, 4, 5. The transformation F : P( ) → P( ) is defined as in Equation (2.4.4), where f1, f2 are contractive projective transformations. The picture of μ∞ represents the fixed point of F. As in other digital pictures of measures, colour intensity values above 255 are replaced by 255.
A picture of part of a measure that is a fixed point of F : P(X) → P(X) with N = 2, as promised by Theorem 1.13.9, is illustrated in Figure 2.24.
Finally we note that quite generally, even when the fn are not contractive, the transformation F : P(X) → P(X) possesses at least one fixed point.
T h e o r e m 2.4.22 |
Let X be a compact metric space. Let fn : X → X be |
continuous for n = 1, |
2, . . . , N in Equation (2.4.4). Then there exists a measure |
μ P(X) that is invariant for F .
P r o o f This follows from the Schauder–Tychenoff fixed-point theorem; see [30], p. 456. It uses the fact that P(X) is a convex, compact, subset of a normed linear space, namely the space of signed Borel measures on X, that is, the space of continuous linear functions from C(X) into R. Moreover the continuity of fn : X → X for n = 1, 2, . . . , N implies that F : P(X) → P(X) is continuous with respect to the weak* topology, which implies that it is continuous in the metric dP .
Two examples of measures μ P( R2) that are fixed points of a continuous transformation that is not contractive are illustrated in Figure 2.25.

2.5 Linear and affine transformations in two and three dimensions 129
Figure 2.23 Approximate pictures of the measures μ0, μ1, μ2, μ3, μ4, μ5, μ6 and μ∞ obtained by recursive application of a transformation F : P( ) → P( ), as in Equation (2.4.4), where f1, f2 are projective transformations.
2.5 Linear and affine transformations in two and three dimensions
In this section we describe the behaviour of linear transformations on R2 and R3. These linear transformations are fundamental to the description of Mobius¨ and projective transformations. We want to know how linear transformations on R2 act on points, sets, pictures, and measures.
As a reminder and to set some notation in place, we begin by recalling a few details from linear algebra. But generally we assume familiarity with vector spaces and linear transformations, including such concepts as inner products and eigenvectors, eigenvalues, adjoints, transposes, and inverses of matrices.
