Преобразования Лоренца
Пусть в начальный момент времени начала
координат системы
и системы K совпадают,
и система
движется относительно системы K
со скоростью V. Тогда
координаты y и z
системы K должны
обращаться в нуль одновременно с
координатами
и
системы
:
,
.
Из условия равноправности этих двух
инерциальных систем отсчёта (первый
постулат теории относительности)
следует, что
и
.
Тогда, перемножив соответственные
уравнения, получим
и
,
или
,
;
,
.
Знак «+» следует из сонаправленности
осей. Таким образом,
,
.
Для координаты x получим:
,
.
В силу равноправности систем K
и
коэффициент в
обоих случаях должен быть один и тот
же. Пусть в момент времени
из начал координат в направлении оси x
посылается световой сигнал, который
производит вспышку света на экране. Это
событие характеризуется в системе K
координатой x, а в
системе
координатой
,
причём
,
.
Подставив эти значения в вышеполученные
формулы, получим соотношения
.
Перемножив эти соотношения и сократив
обе части полученного равенства на
,
придём к уравнению
.
Отсюда
.
Подставив это выражение в формулы для
преобразования координат, получим:
,
.
Формулы преобразования времени получатся
из этих, если исключим из них координаты
и разрешим их относительно времени. В
результате получится:
,
.
Собрав всё это вместе, получим преобразования Лоренца:
.
Вычислим скорость:
;
.
Проделав это для
,
получим преобразования Лоренца для
скорости:
.
Собственное время тела –
это время, отсчитываемое в той системе
отсчёта, где это тело покоится,
.
Собственная длина тела –
длина тела, измеренная в той системе
отчёта, где это тело покоится,
.
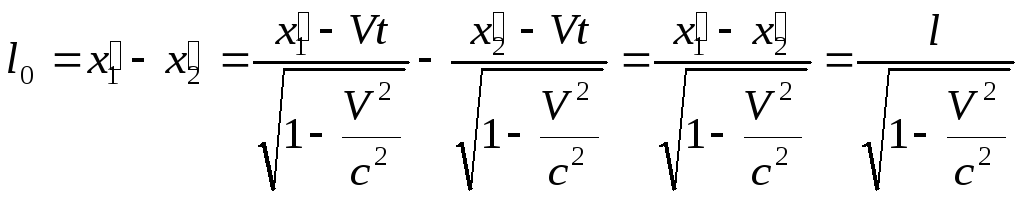Интервал – расстояние между
двумя событиями в четырёхмерном
пространстве-времени.
.
Интервал инвариантен:
.
В зависимости от того, какая составляющая
интервала преобладает, пространственная
или временная, интервал называют
пространственноподобным
или времениподобным
.
В случае
интервал
называют светоподобным. Если интервал
между двумя событиями пространственноподобный,
то всегда можно найти такую систему
отсчёта, где эти события происходят
одновременно:
.
Если же интервал времени подобный, то
можно найти такую систему отсчёта, где
оба эти события происходили в одной
точке:
.
Причинно связанными друг с другом могут
только события, разделёнными
времениподобными или светоподобными
интервалами.
Релятивистская динамика
Исходя из требования сохранения импульса,
релятивистский импульс определяется
как
,
где
- приращение собственного времени тела
и
.
Тогда
.
В релятивистской динамике второй закон
Ньютона остаётся тем же:
.
Таким образом, вектор ускорения в общем
случае не коллинеарен вектору силы.
.
Умножим правую часть равенства на
,
а левую – на равное
произведение
.
В результате получим соотношение
.
Справа стоит элементарная работа
.
Следовательно, левая часть равенства
представляет собой приращение кинетической
энергии тела:
.
Тогда
.
когда скорость равна нулю. Значит,
,
т.е.
и соответственно
.
Выражение
называют полной энергией тела.
Выражение
называют энергией покоя тела. В случае
сложного тела энергия покоя включает
в себя помимо энергий покоя составляющих
его частиц также кинетическую энергию
этих частиц (обусловленную их движением
относительно центра масс тела) и энергию
их взаимодействия друг с другом.
Из сопоставления формул для импульса
и энергии следует, что они связаны
соотношением
,
.
Из этого равенства следует, что выражение
инвариантно.