
Законы сохранения в механике
Закон сохранения импульса:
![]() ,
т.е., если на систему не действуют силы,
то импульс её остаётся постоянным. В
частности, если проекция равнодействующей
силы на вектор импульса равна нулю, то
модуль импульса остаётся постоянным.
Закон сохранения импульса связан с
однородностью пространства: в любой
точке пространства физические явления
будут протекать одинаково.
,
т.е., если на систему не действуют силы,
то импульс её остаётся постоянным. В
частности, если проекция равнодействующей
силы на вектор импульса равна нулю, то
модуль импульса остаётся постоянным.
Закон сохранения импульса связан с
однородностью пространства: в любой
точке пространства физические явления
будут протекать одинаково.
Закон сохранения момента импульса:
![]() ,
т.е., если на систему не действуют силы,
то момент импульса её остаётся постоянным.
В частности, если проекция момента
равнодействующей силы равна нулю, то
модуль момента импульса остаётся
постоянным. Закон сохранения момента
импульса связан с изотропностью
пространства: после поворота системы
на любой угол физические явления будут
протекать одинаково.
,
т.е., если на систему не действуют силы,
то момент импульса её остаётся постоянным.
В частности, если проекция момента
равнодействующей силы равна нулю, то
модуль момента импульса остаётся
постоянным. Закон сохранения момента
импульса связан с изотропностью
пространства: после поворота системы
на любой угол физические явления будут
протекать одинаково.
Закон сохранения энергии:
![]() ,
т.е., если не действуют диссипативные
силы, то суммарная механическая энергия
остаётся постоянной. Закон сохранения
энергии связан с однородностью времени:
в любой момент физические явления будут
протекать одинаково.
,
т.е., если не действуют диссипативные
силы, то суммарная механическая энергия
остаётся постоянной. Закон сохранения
энергии связан с однородностью времени:
в любой момент физические явления будут
протекать одинаково.
Механическая энергия и общие закономерности движения.
П отенциальная
кривая – график зависимости
отенциальная
кривая – график зависимости
![]() .
.
Пусть на графике изображена потенциальная энергия некоторой системы.
Если энергия системы равна
![]() ,
то в точке А система двигаться не
может, т.к.
,
то в точке А система двигаться не
может, т.к.
![]() и
и
![]() ,
следовательно
,
следовательно
![]() ,
т.е.
,
т.е.
![]() .
.
Если энергия системы равна
![]() ,
то в точке E с
система находится в неустойчивом
равновесии: любое увеличение энергии
«свалит» её либо к точке D,
либо к точке F.
,
то в точке E с
система находится в неустойчивом
равновесии: любое увеличение энергии
«свалит» её либо к точке D,
либо к точке F.
Если энергия системы равна
![]() ,
и система находится в точке B
или D, то она будет
совершать колебания от B
к D, а если она находится
в точке F, то будет
двигаться в сторону +
по оси x.
,
и система находится в точке B
или D, то она будет
совершать колебания от B
к D, а если она находится
в точке F, то будет
двигаться в сторону +
по оси x.
Если энергия системы равна C, то система не двигается.
BCD называется потенциальной ямой, а DEF – потенциальным барьером.
Точки A, C и E – точки останова, точка C- точка устойчивого равновесия, точка E – неустойчивого равновесия.
Фазовая плоскость – это
плоскость, точки которой являются
совокупностью значений координаты и
импульса (![]() ,
иногда
,
иногда
![]() ).
).
Совокупность фазовых точек – фазовая траектория.
Столкновение двух тел
Столкновение тел: взаимодействие двух или более тел, которые происходят в ограниченной области пространства и в ограниченный промежуток времени.
Удар – столкновение, при котором импульсы тел изменяются без изменения координат.
Если система тел изолирована, то исходя
из законов сохранения
![]() ,
,
![]() ,
,
![]() .
.
Абсолютно упругий удар: удар, при котором сохраняется полная механическая энергия и импульс. После удара тела движутся с разными скоростями.
Абсолютно неупругий удар: удар, при котором сохраняется только импульс, а часть механической энергии переходит во внутреннюю. После удара тела движутся с одинаковыми скоростями в одном направлении («слипаются»).
Центральный удар: удар, происходящий вдоль прямой, соединяющий центры масс тел.
П усть
сталкиваются два тела, и при этом
происходит абсолютно упругий удар.
Массы тел
усть
сталкиваются два тела, и при этом
происходит абсолютно упругий удар.
Массы тел
![]() и
и
![]() соответственно, скорости -
соответственно, скорости -
![]() и
и
![]() .
Тогда
.
Тогда
![]() ,
,
![]() ,
т.е.
,
т.е.
![]() ,
,
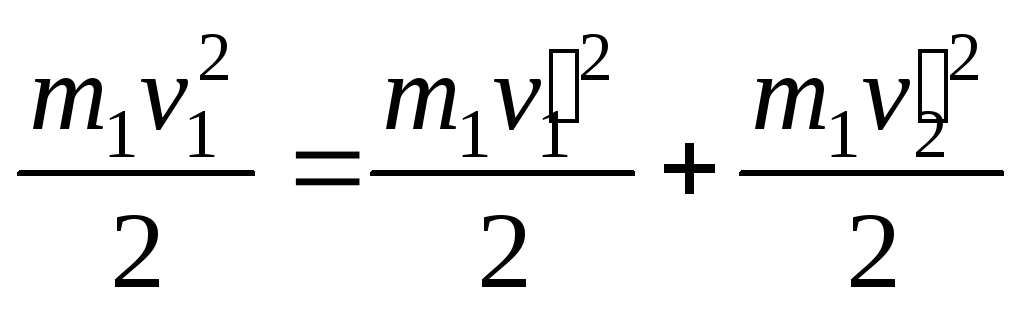 .
Перейдём в систему центра масс и построим
векторную диаграмму импульсов.
.
Перейдём в систему центра масс и построим
векторную диаграмму импульсов.
![]() .
Аналогично
.
Аналогично
![]() .
Теперь изобразим вектор
.
Теперь изобразим вектор
![]() отрезком AB, затем
векторы
отрезком AB, затем
векторы
![]() и
и
![]() ,
каждый из которых представляет собой
сумму двух векторов. Это построение
справедливо вне зависимости от угла .
Значит, точка C может
находиться только на окружности радиуса
,
каждый из которых представляет собой
сумму двух векторов. Это построение
справедливо вне зависимости от угла .
Значит, точка C может
находиться только на окружности радиуса
![]() с центром в точке O,
которая делит отрезок AB
на две части в отношении
с центром в точке O,
которая делит отрезок AB
на две части в отношении
![]() .
Эта окружность есть геометрическое
место положений вершины C
треугольника импульсов ABC,
стороны AC и CB
которого представляют собой импульсы
частиц после столкновения во внешней
системе отсчёта. В зависимости от
соотношения масс точка A
может находиться как внутри, так и вне
окружности. Тогда угол рассеяния
налетающей частицы
.
Эта окружность есть геометрическое
место положений вершины C
треугольника импульсов ABC,
стороны AC и CB
которого представляют собой импульсы
частиц после столкновения во внешней
системе отсчёта. В зависимости от
соотношения масс точка A
может находиться как внутри, так и вне
окружности. Тогда угол рассеяния
налетающей частицы
![]() и угол разлёта частиц
будут такими:
и угол разлёта частиц
будут такими:
 ,
,
где![]() - предельный угол. Он определяется
формулой
- предельный угол. Он определяется
формулой
![]() .
Кроме того, при
.
Кроме того, при
![]() под одним и тем же углом
под одним и тем же углом
![]() возможно рассеяние частицы
возможно рассеяние частицы
![]() как с импульсом
как с импульсом
![]() ,
так и с импульсом
,
так и с импульсом
![]() ,
т.е. в этом случае решение неоднозначно.
,
т.е. в этом случае решение неоднозначно.
Механика твердого тела
Абсолютно твёрдое тело – это протяжённое тело, расстояние между двумя точками которого неизменно.
В дискретной модели твёрдое тело представляется как большая совокупность точечных тел, находящихся на неизменных расстояниях друг от друга, а непрерывная модель рассматривает твёрдое тело как непрерывную среду, в которой можно пренебречь внутренней структурой.
Произвольное движение твёрдого тела
можно представить как суперпозицию
двух движений: поступательного центра
масс и вращательного:
![]() .
.
Теорема Эйлера: Произвольное мгновенное движение твёрдого тела можно представить как сумму мгновенных поступательного и вращательного движений тела в каждый момент времени.
Д вижение
твёрдого тела, при котором одна из его
точек остаётся неподвижной называется
вращением вокруг неподвижной точки
(центра). Это движение в каждый момент
времени можно рассматривать как вращение
вокруг мгновенной оси вращения, проходящей
через неподвижную точку. Чтобы
определить положение тела, вращающегося
вокруг неподвижной точки, в пространстве
обычно пользуются тремя углами
вижение
твёрдого тела, при котором одна из его
точек остаётся неподвижной называется
вращением вокруг неподвижной точки
(центра). Это движение в каждый момент
времени можно рассматривать как вращение
вокруг мгновенной оси вращения, проходящей
через неподвижную точку. Чтобы
определить положение тела, вращающегося
вокруг неподвижной точки, в пространстве
обычно пользуются тремя углами
![]() ,
которые называют углами Эйлера. Угол
называют углом чистого вращения, угол
- углом прецессии, угол
- углом нутации. Тогда проекции
угловой скорости вращения на оси
координат будут такие:
,
которые называют углами Эйлера. Угол
называют углом чистого вращения, угол
- углом прецессии, угол
- углом нутации. Тогда проекции
угловой скорости вращения на оси
координат будут такие:
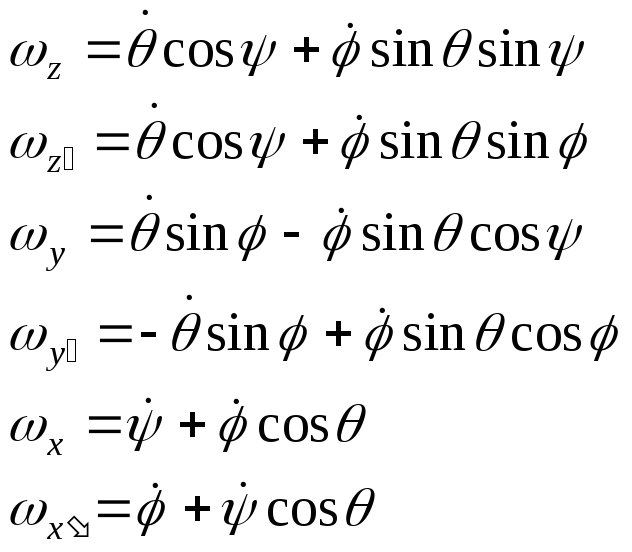
Таким образом, чтобы описать движение твёрдого тела достаточно описать движение трёх его точек, не лежащих на оной прямой.
Точка, скорость которой в рассматриваемом сечении тела равна 0, называется мгновенным центром скоростей.
Если при плоском движении твёрдого тела его угловая скорость отлична от нуля, то в каждый момент времени в рассматриваемом сечении тела имеется единственная точка, скорость которой равна 0. Скорости остальных точек определяются как скорости мгновенного вращательного движения относительно мгновенной оси вращения.
Н айдём
положение мгновенного центра скоростей
относительно точки A.
айдём
положение мгновенного центра скоростей
относительно точки A.
 ,
,
![]() ,
,
![]() .
Помножив обе части уравнения на
.
Помножив обе части уравнения на
![]() ,
получим:
,
получим:
![]() ,
,
![]() .
.
Кинематика движений твёрдого тела с одной неподвижной точкой
Теорема Эйлера: Твёрдое тело, имеющее одну неподвижную точку, может быть переведено из начального положение в произвольное путём поворота вокруг оси, проведённой через эту точку.
При вращении тела на конечные углы результат зависит от последовательности поворотов, в отличие от бесконечно малых углов.
Пусть
![]() - вектор угла поворота, а
- вектор угла поворота, а
![]() - соответствующая хорда и пусть
- соответствующая хорда и пусть
![]() .
Тогда
.
Тогда
![]() (т.к.
(т.к.
![]() совпадает с
совпадает с
![]() )
и
)
и
![]() ,
т.е.
,
т.е.
![]() .
.
Теорема о сложении угловых
скоростей вращения твёрдого тела: Если
тело вращается со скоростью
![]() ,
то это вращение можно представить как
сумму двух вращений со скоростями
,
то это вращение можно представить как
сумму двух вращений со скоростями
![]() и
и
![]() .
.
Тензор моментов инерции твёрдого тела
Моментом инерции материальной
точки относительно какой-либо оси
называется величина
![]() ,
где m
– масса точки, а R
– расстояние от неё до этой оси. Моментом
инерции тела или системы тел относительной
какой-либо оси вращения называется
сумма моментов инерций всех материальных
точек относительно этой оси:
,
где m
– масса точки, а R
– расстояние от неё до этой оси. Моментом
инерции тела или системы тел относительной
какой-либо оси вращения называется
сумма моментов инерций всех материальных
точек относительно этой оси:
![]() .
Тогда момент импульса
.
Тогда момент импульса
![]() .
Момент инерции тела относительно оси
x прямоугольной
декартовой системы координат
.
Момент инерции тела относительно оси
x прямоугольной
декартовой системы координат
![]() .
Центробежным моментом инерции для оси
z называется величина
.
Центробежным моментом инерции для оси
z называется величина
![]() .
.
Тензор инерции:
 .
.
Главные оси симметрии
твёрдого тела – это оси, относительно
которых тензор инерции твёрдого тела
имеет диагональный вид, т.е.
 .
.
Если тело однородно, то
![]() .
В декартовой системе координат
.
В декартовой системе координат
![]() ,
в цилиндрической
,
в цилиндрической
![]() ,
в сферической
,
в сферической
![]() .
.
Главный момент инерции некоторых однородных тел простейшей формы (m – масса тела):
-
Прямолинейный тонкий стержень длиной l, расположенный вдоль оси Oz:
 ,
,
 .
. -
Прямоугольный параллелепипед со сторонами a, b и c, параллельными соответственно Ox, Oy и Oz:

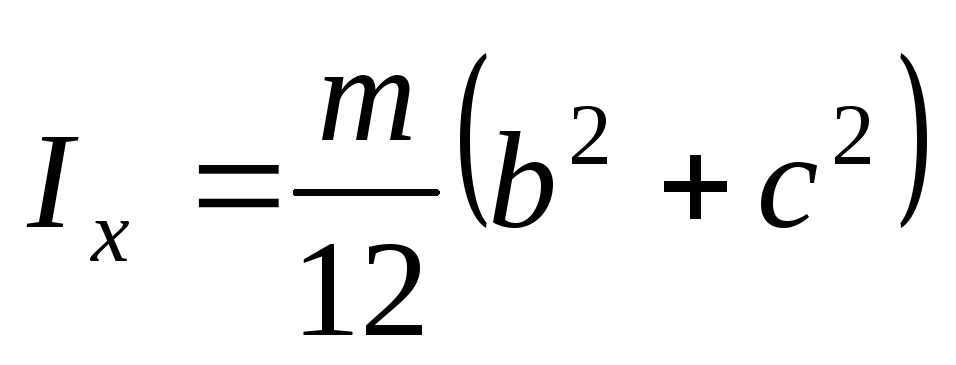 ,
,
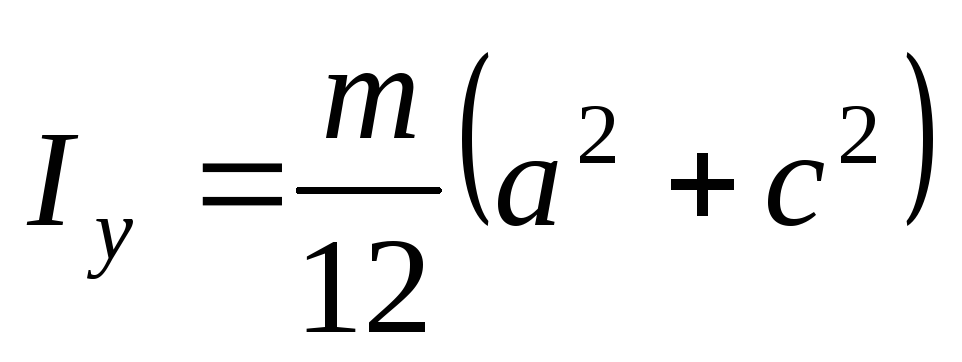 ,
,
 .
. -
Полый прямой круглый цилиндр высотой H и радиусами внешней и внутренней поверхностей, равными
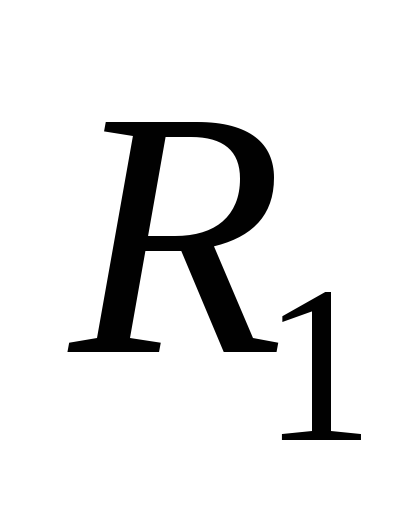 и
и
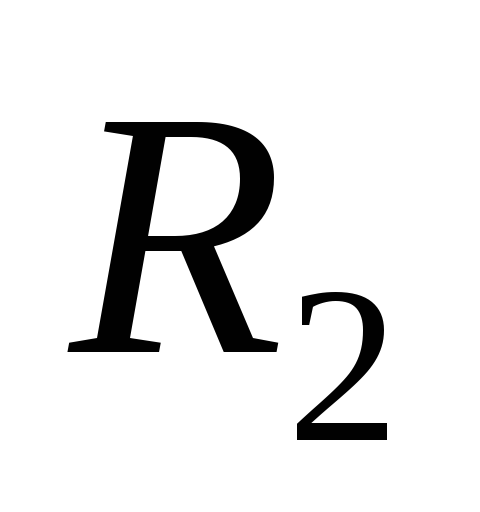 ;
Oz – ось цилиндра:
;
Oz – ось цилиндра:
 ,
,
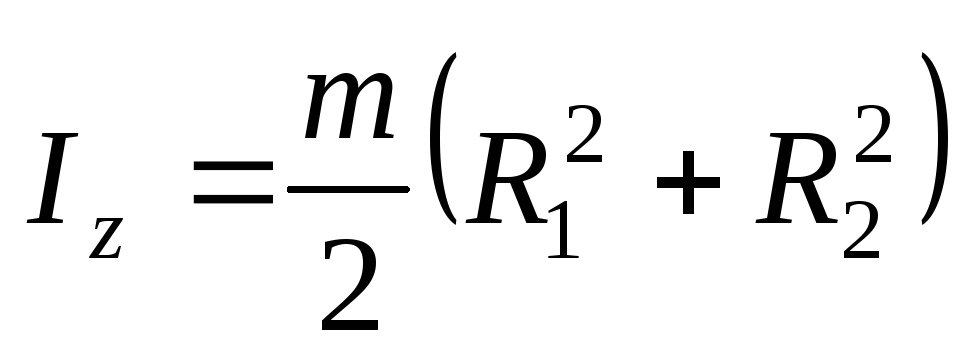 .
. -
Полый шар с радиусами внешней и внутренней поверхностей, равными
 и
и
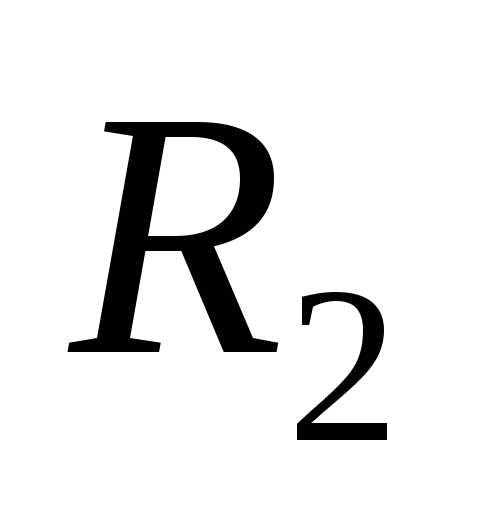 :
:
 ,
для сплошного шара:
,
для сплошного шара:
 ,
для тонкостенной сферы:
,
для тонкостенной сферы: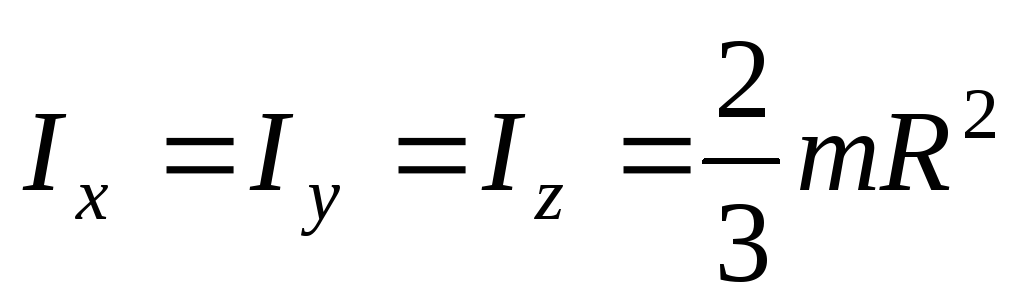 ,
для шарового сектора (Oz
– ось симметрии):
,
для шарового сектора (Oz
– ось симметрии):
 ,
где h – высота
шарового сегмента, принадлежащего
шаровому сектору, для шарового сегмента
(Oz – ось симметрии):
,
где h – высота
шарового сегмента, принадлежащего
шаровому сектору, для шарового сегмента
(Oz – ось симметрии):
 .
. -
Прямой круглый конус радиусом основания R высотой H (Oz – ось конуса):
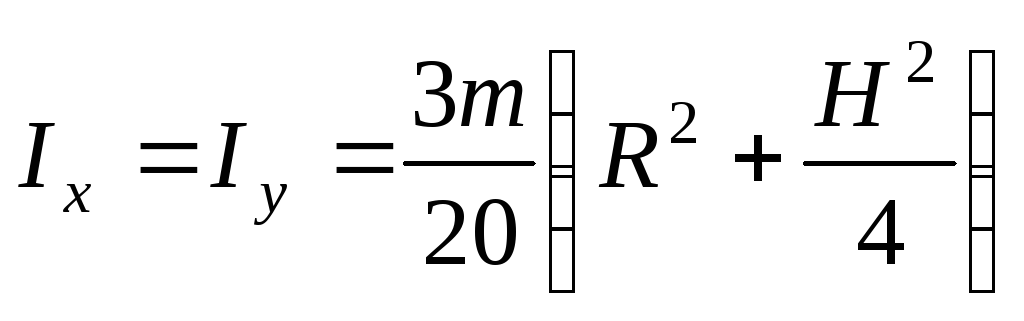 ,
,
 ,
для боковой поверхности тонкостенного
полого конуса:
,
для боковой поверхности тонкостенного
полого конуса:
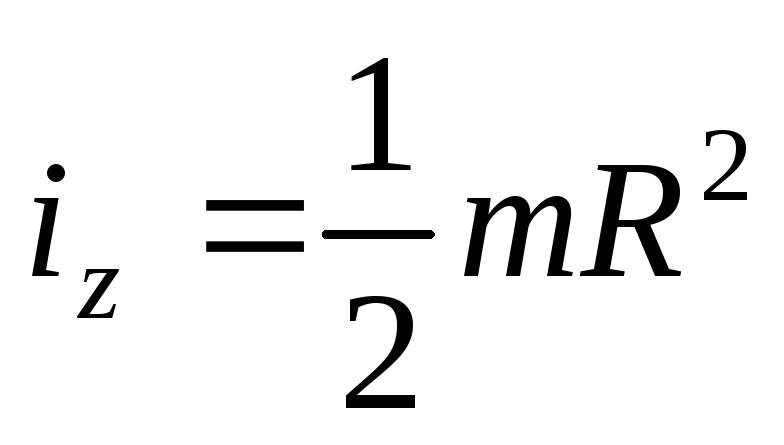 .
. -
Усечённый прямой круглый конус высотой H и радиусами оснований
 и
и
 (Oz – ось конуса):
(Oz – ось конуса):
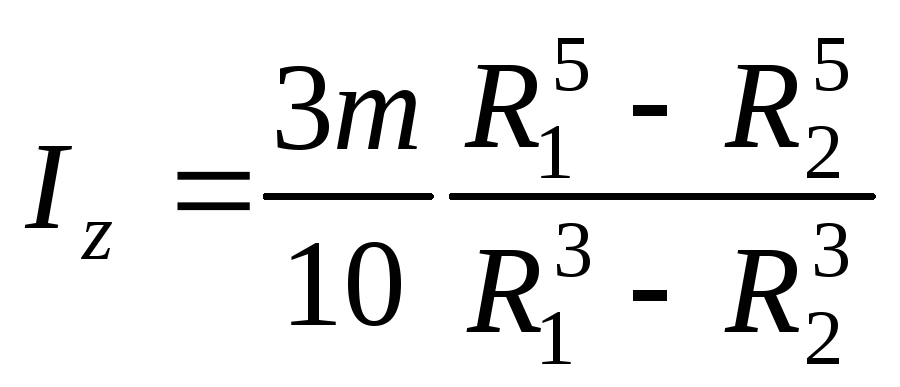 ,
для боковой поверхности тонкостенного
усечённого конуса:
,
для боковой поверхности тонкостенного
усечённого конуса:
 .
. -
Прямая прямоугольная пирамида высотой H, стороны основания a и b параллельны соответственно осям Ox и Oy:
 ,
,
 ,
,
 .
. -
Эллипсоид с полуосями a, b и c, параллельными соответственно осям Ox, Oy и Oz:
 ,
,
 ,
,
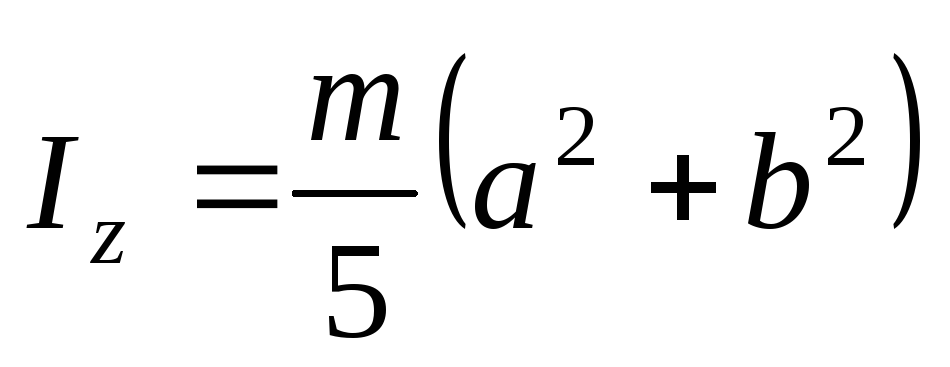 .
. -
Кольцо радиуса R с круглым поперечным сечением радиуса r (тор); ось Oz перпендикулярна к плоскости, в которой лежат центры поперечных сечений:
 ,
,
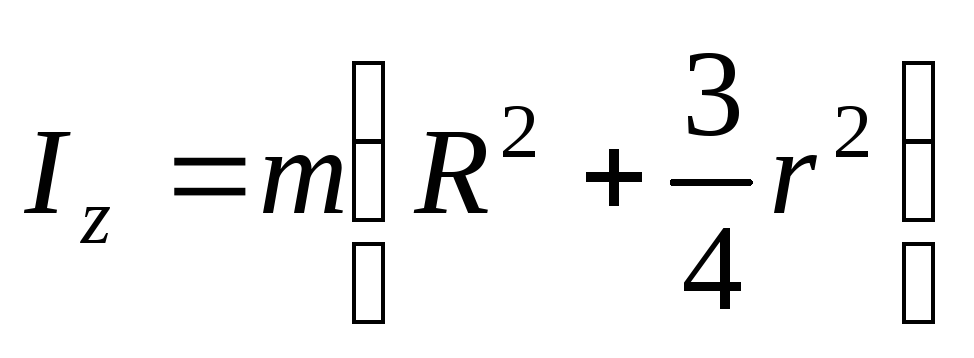 .
.
