
Физика
I семестр.
Классическая механика
Предмет механики.
-
Механика – наука о механическом движении, которое состоит в изменении положения тел или их частей в пространстве с течением времени.
-
Материальная точка – тело, размеры и форма которого несущественны в данной задаче. Это математическая точка, обладающая массой.
-
Абсолютно твёрдое тело – тело, расстояние между двумя точками которого постоянно.
-
Система отсчёта – реальное или условное тело, с которым жёстко связана система координат и синхронизированных между собой часов.
-
Изолированная система тел – модель, система тел, которые движутся только под действием внутренних сил, а внешние силы либо отсутствуют, либо их действия скомпенсированы. Систему тел можно считать изолированной, если силы взаимодействия с внешними телами намного меньше внутренних сил.
Пространство и время в классической механике.
Свойства абсолютного времени:
-
Время существует само по себе и своим существованием не обязано чему-либо в мире.
-
Ходу времени подчиняются все физические тела, но эти тела не могут оказывать какое-либо влияние на время.
-
Все промежутки времени равноправны.
-
Время простирается неограниченно далеко в прошлое и в будущее.
Свойства абсолютного пространства:
-
Пространство всё вмещает в себя, везде одинаково и неизменно.
-
Пространство существует само по себе и этим ничему не обязано.
-
Пространство включает в себя все тела, не испытывая воздействия с их стороны.
-
Все точки и направления пространства равноправны.
-
Пространство бесконечно и имеет три измерения.
Пространство и время не зависят и не влияют друг на друга.
Пространство однородно (все его точки эквивалентны, все физические процессы в каждой точке протекают одинаково) и изотропно (протекание процессов не зависит от направления). Время однородно.
Кинематика точечного тела.
Кинематика – это раздел механики, посвящённый изучению и математическому описанию механического движения, не исследующий причины возникновения этого движения.
Траектория – линия, которое описывает тело в пространстве при движении.
Существуют три способа задания движения: векторный, координатный и естественный.
-
Векторный (основной способ). Положение точки определяется вектором, проведённым из начала координат в местоположение тела (этот вектор называют радиус-вектором). Радиус вектор есть некоторая функция от времени:
 .
.
Перемещение – вектор,
направленный из начального положения
точки в конечное:
![]()
Путь – сумма длин всех участков траектории, пройденных телом за рассматриваемый промежуток времени.
Скорость характеризует направление и быстроту изменения радиус-вектора.
Средняя скорость – это
вектор, равный отношению перемещения
к промежутку времени, за который оно
произошло:
![]() .
.
Мгновенная скорость:
![]() .
.
Вектор мгновенной скорости направлен по касательной к траектории.
Среднее ускорение – отношение
изменения скорости к промежутку времени,
за который это изменение произошло:
![]() .
.
Мгновенное ускорение:
![]()
В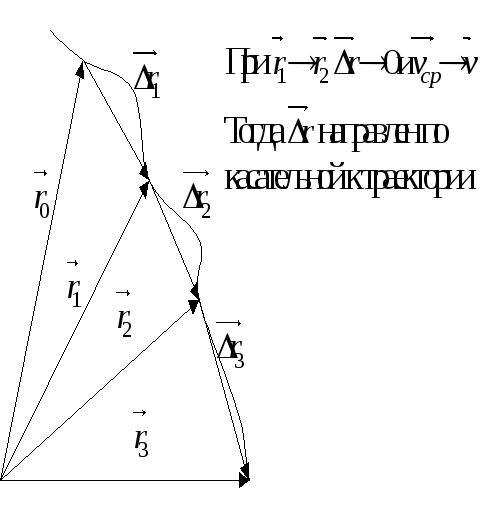 ектор
мгновенного ускорения направлен по
касательной к линии, которую описывает
вектор скорости (годографу).
ектор
мгновенного ускорения направлен по
касательной к линии, которую описывает
вектор скорости (годографу).
-
Координатный способ: С телом жёстко связывают какую-либо систему координат: декартову, цилиндрическую или сферическую и положение точки описывается тремя её координатами:
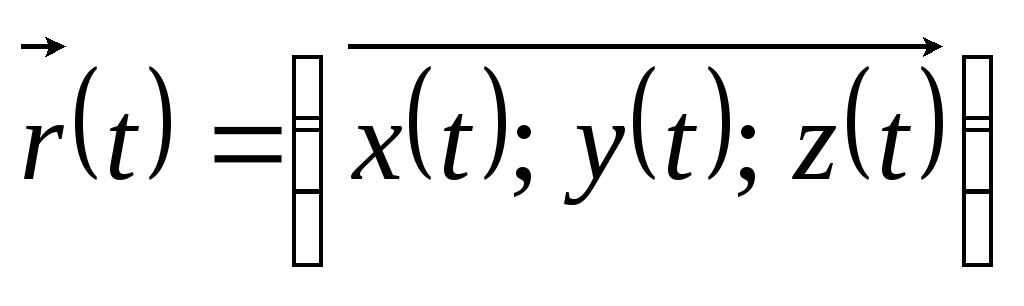 ,
т.е.
,
т.е.
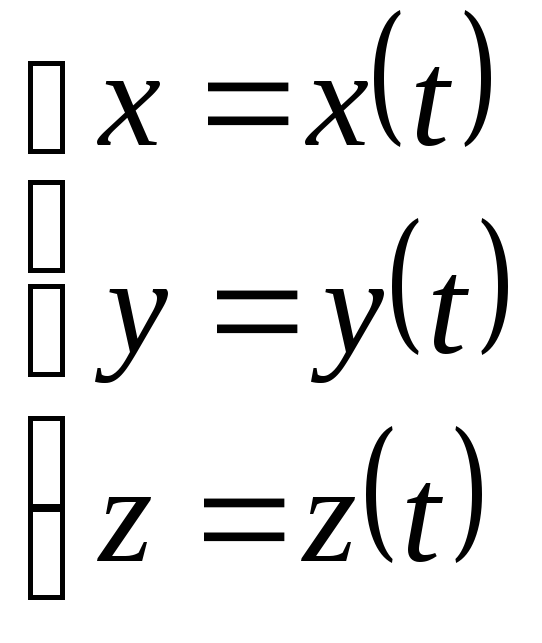 .
Тогда
.
Тогда
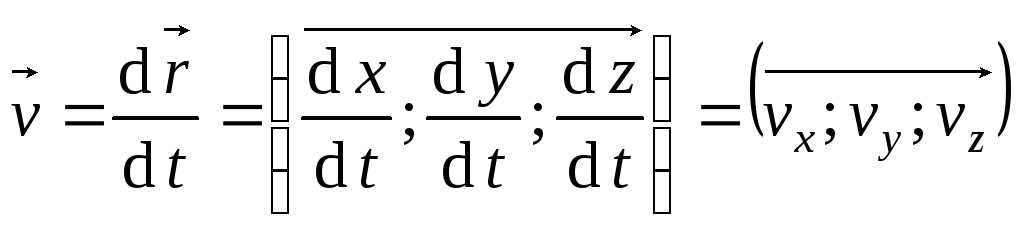 ,
а
,
а
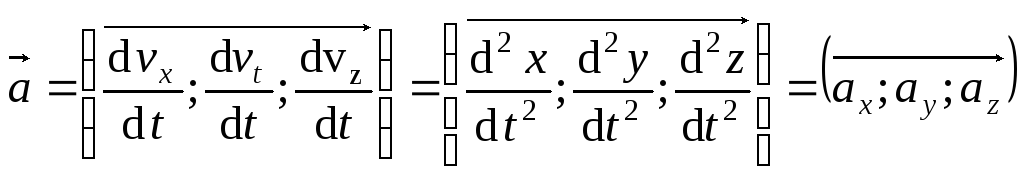 .
В цилиндрической системе координат:
.
В цилиндрической системе координат:
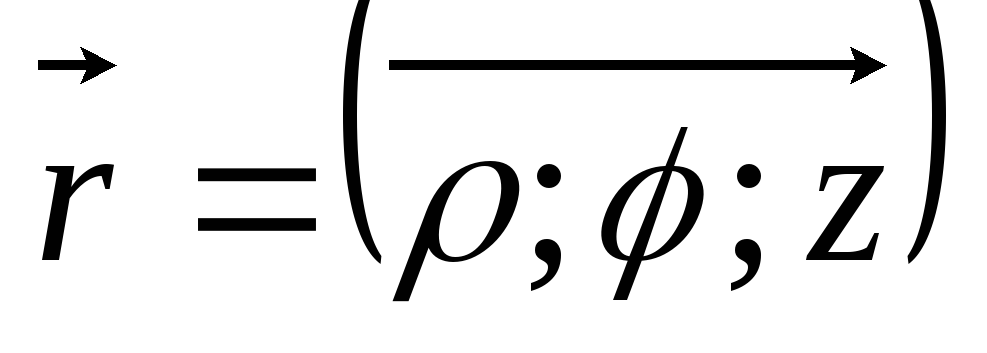 ,
,
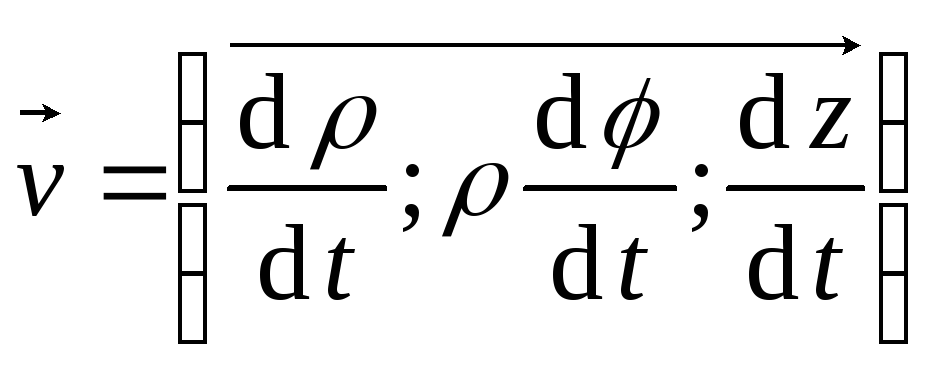 ,
,
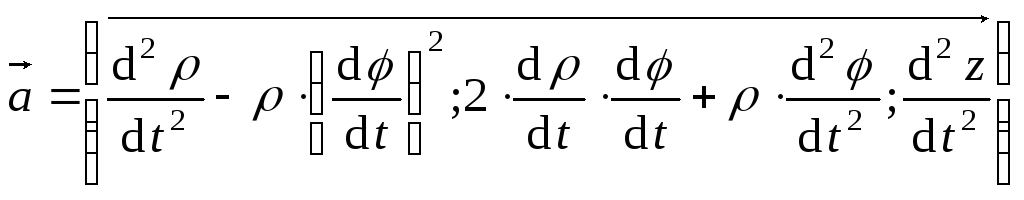 .
В сферической:
.
В сферической:
 ,
,
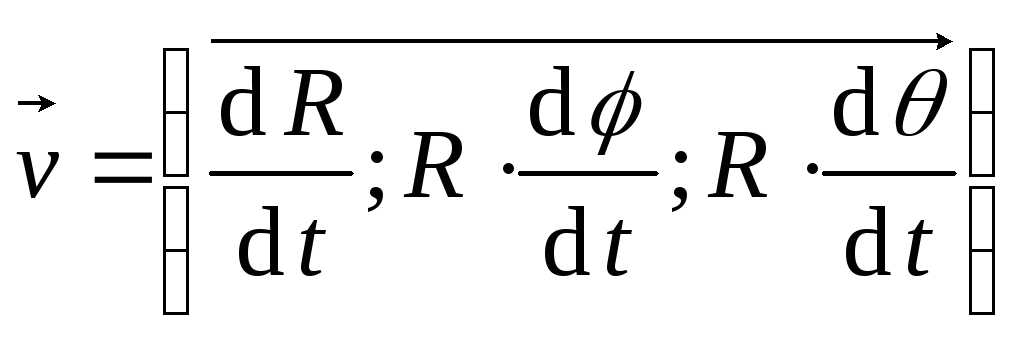 ,
,
 .
. -
Е
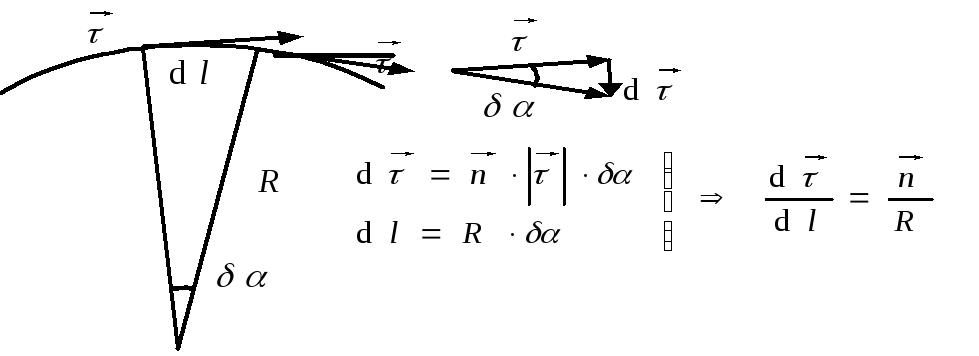 стественный
способ: на траектории тела выбирается
начало отсчёта и задаётся единичный
отрезок. Тогда положение точки в
пространстве характеризуется её
положением на траектории, и оно
определено, если известна зависимость
стественный
способ: на траектории тела выбирается
начало отсчёта и задаётся единичный
отрезок. Тогда положение точки в
пространстве характеризуется её
положением на траектории, и оно
определено, если известна зависимость
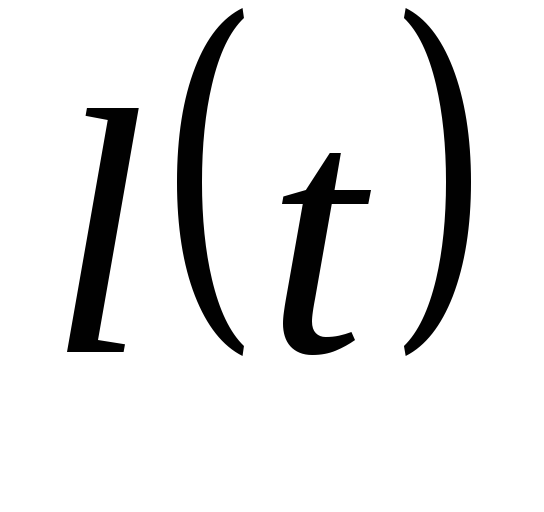 ,
где l – расстояние
от начала отсчёта до точки вдоль
траектории. Пусть
,
где l – расстояние
от начала отсчёта до точки вдоль
траектории. Пусть
 ,
где
,
где
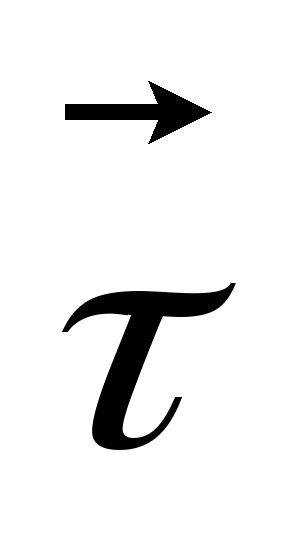 - единичный вектор, направленный по
касательной к траектории. Тогда
- единичный вектор, направленный по
касательной к траектории. Тогда
 где
вектор
где
вектор
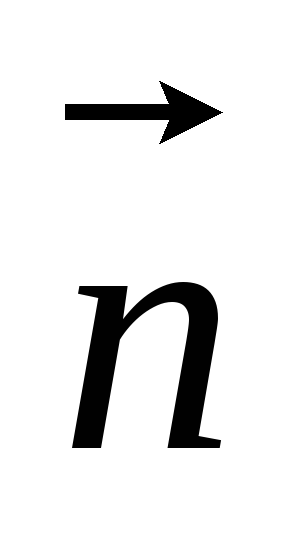 - вектор, направленный перпендикулярно
траектории к центру окружности в данной
точке.
- вектор, направленный перпендикулярно
траектории к центру окружности в данной
точке.
Кривизна траектории
![]() ,
R
– радиус окружности в этой точке. Если
известно
,
R
– радиус окружности в этой точке. Если
известно
![]() ,
то
,
то
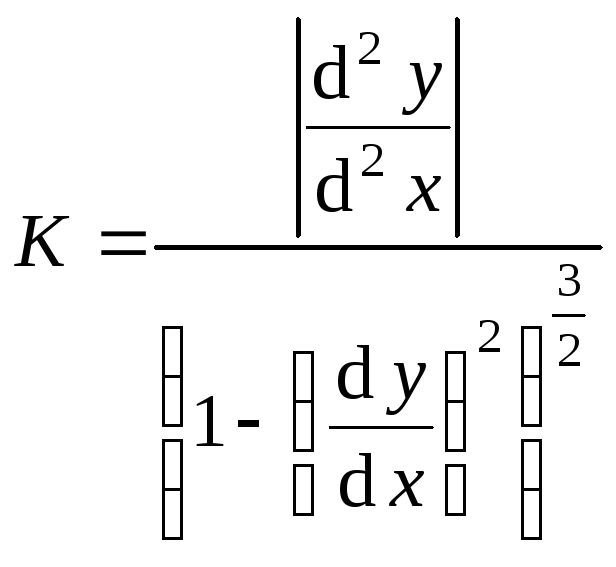 .
.
Классический детерминизм в механике: существует строгая однозначная связь между физическими величинами, характеризующими состояние системы в начальный момент времени и их значениями в любой последующий момент. К примеру, зная функцию радиус вектора от времени можно рассчитать скорость и ускорение тела в любой момент времени.
Равномерное прямолинейное
движение – это движение с постоянной
скоростью, т.е.
![]() .
При этом
.
При этом
![]() ,
,
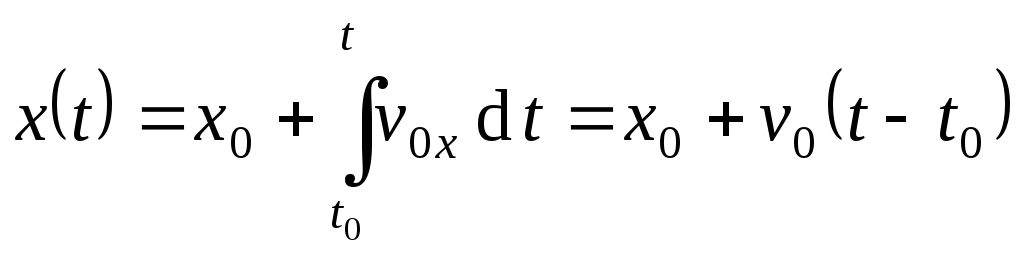
Равноускоренное движение
– это движение, при котором ускорение
постоянно, т.е.
![]() .
Тогда
.
Тогда
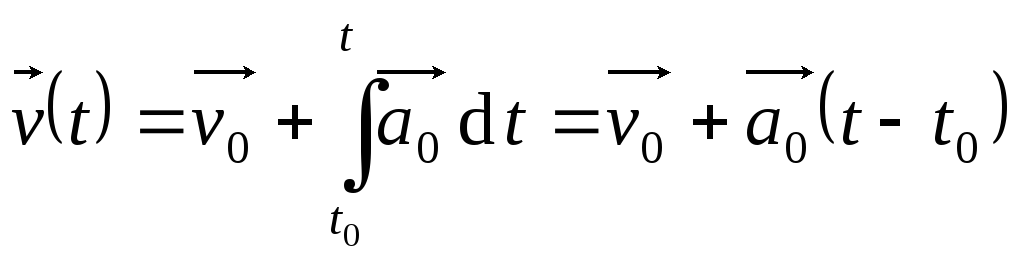 ,
,
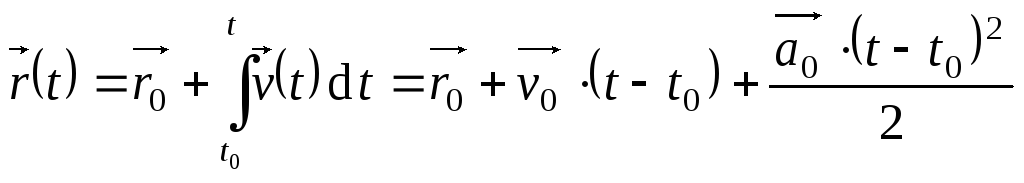 .
.
Вращательное движение
Путь по окружности постоянного радиуса
вращается точка. Ось вращения
– это прямая, проходящая через центр
окружности и перпендикулярная плоскости,
в которой она лежит. Вектор элементарного
поворота
![]() –
это вектор, направление которого
определяется по правилу правого винта,
а длина численно равна углу поворота.
Пусть за время
–
это вектор, направление которого
определяется по правилу правого винта,
а длина численно равна углу поворота.
Пусть за время
![]() тело,
двигаясь по окружности, совершило
поворот. Тогда
тело,
двигаясь по окружности, совершило
поворот. Тогда
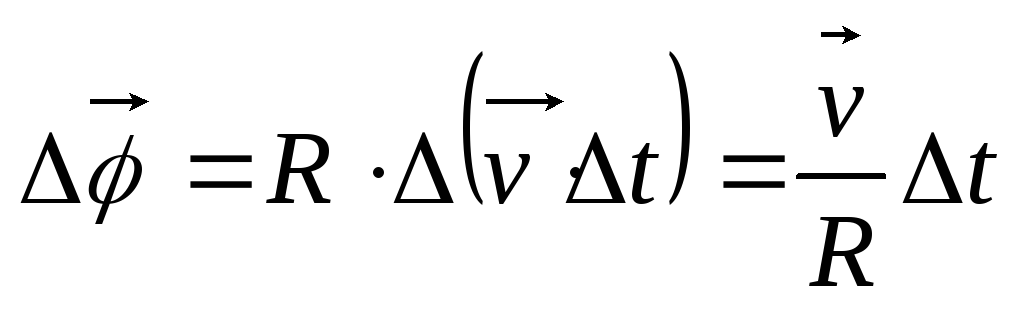 .
Величина, характеризующая темп изменения
угла поворота, называется средней
угловой скоростью:
.
Величина, характеризующая темп изменения
угла поворота, называется средней
угловой скоростью:
![]() .
Мгновенная угловая скорость
.
Мгновенная угловая скорость
![]() .
Угловое ускорение характеризует темп
изменения угловой скорости:
.
Угловое ускорение характеризует темп
изменения угловой скорости:
![]() ;
;
![]() .
.
Кинематика относительного вращательного движения
Принцип независимости движений: любое движение тела может быть представлено в виде суперпозиции двух или более независимых движений, определяемых в различных системах отсчёта.
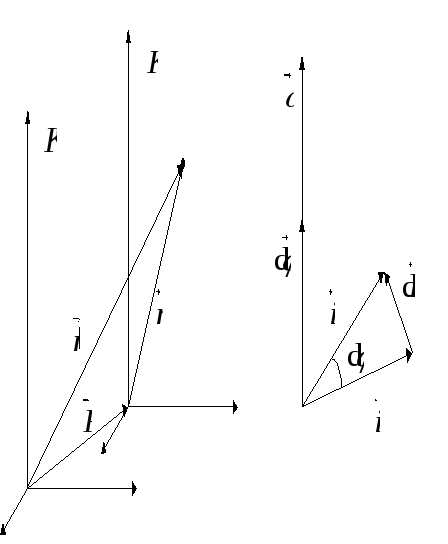
Пусть система К движется относительно
инерциальной системы
![]() с ускорением
с ускорением
![]() ,
и вращается с угловым ускорением
,
и вращается с угловым ускорением
![]() ,
и движется тело с ускорением
,
и движется тело с ускорением
![]() относительно системы
относительно системы
![]() .
Требуется найти зависимость радиус-вектора,
скорости и ускорения тела в неинерциальной
системе отсчёта через аналогичные
величины в инерциальной. Из рисунка
видно, что в любой момент времени
выполняется равенство
.
Требуется найти зависимость радиус-вектора,
скорости и ускорения тела в неинерциальной
системе отсчёта через аналогичные
величины в инерциальной. Из рисунка
видно, что в любой момент времени
выполняется равенство
![]() .
Тогда
.
Тогда
![]() .
Пусть теперь система K
за время
.
Пусть теперь система K
за время
![]() повернулась
на угол
повернулась
на угол
![]() .
Отсюда следует
.
Отсюда следует
![]() .
Подставив это в выражение для скорости,
мы получим:
.
Подставив это в выражение для скорости,
мы получим:
![]() .
.
![]() Продифференцировав
ещё раз, получим ускорение:
Продифференцировав
ещё раз, получим ускорение:

Ускорение
![]() называют кориолесовым ускорением. Оно
обусловлено движением тела относительно
вращающейся системы отсчёта.
называют кориолесовым ускорением. Оно
обусловлено движением тела относительно
вращающейся системы отсчёта.
Ускорение
![]() называют центростремительным ускорением.
называют центростремительным ускорением.
Динамика точечного тела
Принцип относительности Галилея
Состояние движения: состояние тела, характеризуемое определённым положением и скоростью.
Динамика – раздел механики, изучающий причины изменения состояния движения тел. Прямая задача динамики заключается в нахождении законов движения тел, если известны силы, действующие на тела и их начальные состояния. Обратная задача: по известному движению тел определить, под действием каких сил происходит это движение.
Инерциальная система отсчёта – это система отсчёта, относительно которой любое невзаимодействующее тело будет сохранять состояние своего движения (покоя). Систему отсчёта можно считать неинерциальной в некоторой области пространства в течение некоторого промежутка времени, если во всей этой области и в течение всего промежутка времени тело не изменяет состояние своего движения.
Преобразования Галилея: Пусть одна
система отсчёта движется относительно
другой равномерно и прямолинейно со
скоростью
![]() и в этой системе движется тело со
скоростью
и в этой системе движется тело со
скоростью
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.
Принцип относительности Галилея: законы механики имеют одинаковый вид во всех инерциальных системах отсчёта.
