
- •11 Клас. Р і ч н а к о н т р о л ь н а р о б о т а
- •11 Клас. Р і ч н а к о н т р о л ь н а р о б о т а
- •11 Клас. Р і ч н а к о н т р о л ь н а р о б о т а
- •11 Клас. Р і ч н а к о н т р о л ь н а р о б о т а
- •11 Клас. Р і ч н а к о н т р о л ь н а р о б о т а Варіант 5
- •11 Клас. Р і ч н а к о н т р о л ь н а р о б о т а Варіант 6
- •11 Клас. Р і ч н а к о н т р о л ь н а р о б о т а Варіант 7
- •11 Клас. Р і ч н а к о н т р о л ь н а р о б о т а Варіант 8
- •11 Клас. Р і ч н а к о н т р о л ь н а р о б о т а Варіант 9
- •11 Клас. Р і ч н а к о н т р о л ь н а р о б о т а Варіант 10
- •11 Клас. Р і ч н а к о н т р о л ь н а р о б о т а Варіант 11
- •11 Клас. Р і ч н а к о н т р о л ь н а р о б о т а Варіант 12
11 Клас. Р і ч н а к о н т р о л ь н а р о б о т а
Варіант 3
|
№№ |
3 бали |
6 балів |
9 балів |
12 балів |
|
Ліва сторона | ||||
|
№1. |
Висота рівностороннього циліндра 10 см. Знайдіть бічну поверхню. |
Площа
осьового перерізу циліндра дорівнює
|
У циліндрі паралельно до його осі проведено переріз, діагональ якого утворює з площиною нижньої основи кут φ. Цей переріз перетинає основу по хорді, яка стягує дугу α. Визначте бічну поверхню циліндра, якщо радіус його основи дорівнює R. |
Хорда основи циліндра дорівнює а і стягує дугу кола основи величиною α. Площа перерізу, проведеного через цю хорду перпендикулярно до площини основи, дорівнює S. Знайдіть площу повної поверхні циліндра. |
|
№2. |
Куля радіусом 5 см перетнута площиною на відстані 3 см. Знайдіть радіус перерізу. |
У кулі на відстані 8 см від його центру проведено переріз, площа якого 36π см2. Знайдіть радіус кулі. |
На
відстані
|
Радіус
кулі
дорівнює
|
|
№3. |
Яка формула виражає об’єм правильної трикутної призми із стороною основи а і висотою Н ? а)
в)
|
Всі
ребра прямої трикутної призми мають
довжину
|
У
похилій трикутній призмі сторони
основи дорівнюють
4, 13 і
15 см. Бічне
ребро –
|
В основі прямої призми лежить рівнобедрений трикутник з кутом β при основі і радіусом вписаного кола r. Діагональ бічної грані, що містить основу цього трикутника, утворює кут α з площиною основи призми. Знайдіть об’єм призми. |
Права сторона
|
№1. |
Площа осьового перерізу циліндру дорівнює Q. Знайдіть бічну поверхню. |
Площа бічної поверхні циліндра дорівнює 16π см2. Знайдіть площу осьового перерізу циліндра. |
У
нижній основі циліндра проведена
хорда, довжина якої дорівнює
а.
Ця
хорда стягує дугу
|
Хорда
основи
циліндра стягує дугу основи, яка
дорівнює
|
|
№2. |
Куля перетнута площиною на відстані 20 см від центра. Знайдіть радіус перерізу, якщо радіус кулі дорівнює 25 см. |
Через кінець радіуса кулі проведено переріз, який утворює з цим радіусом кут 60о. Знайдіть радіус кулі, якщо площа перерізу 64π см2. |
На
відстані
|
Через
кінці
трьох взаємноперпендикулярних радіусів
проведено переріз кулі. Радіус кулі
дорівнює
|
|
№3. |
Яка формула виражає об’єм правильної чотирикутної призми зі стороною а та висотою Н ? а)
а2Н;
б)
|
Об’єм
прямої призми, основа якої – правильний
трикутник, дорівнює
|
В основі похилої призми лежить паралелограм зі сторонами 6 дм і 12 дм і гострим кутом 60о. Бічне ребро призми дорівнює 14 дм і утворює з площиною основи кут 30о. Обчисліть об’єм призми. |
В основі прямої призми лежить рівнобедрений трикутник з кутом α при вершині і радіусом описаного кола R. Діагональ бічної грані, що містить бічну сторону цього трикутника, утворює з площиною основи кут β. Знайдіть об’єм призми. |

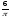 см2.
Знайдіть
площу бічної поверхні циліндра.
см2.
Знайдіть
площу бічної поверхні циліндра.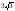 смвід
центру кулі проведено переріз, довжина
кола якого у 2 рази менша від довжини
більшого кола. Знайдіть площу перерізу.
смвід
центру кулі проведено переріз, довжина
кола якого у 2 рази менша від довжини
більшого кола. Знайдіть площу перерізу.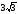 см.
Черезкінці
трьох радіусів, любі два з яких
перетинаються під кутом
60о,
проведено
переріз кулі. Знайдіть площу перерізу.
см.
Черезкінці
трьох радіусів, любі два з яких
перетинаються під кутом
60о,
проведено
переріз кулі. Знайдіть площу перерізу.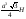 ;
б)
;
б)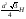 ;
;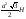 ?
?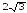 см.Знайдіть
об’єм призми.
см.Знайдіть
об’єм призми.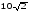 см
нахилене
до площини основи під кутом
45о.
Обчисліть
об’єм призми.
см
нахилене
до площини основи під кутом
45о.
Обчисліть
об’єм призми. .Відрізок,
який сполучає центр верхньої основи
з серединою проведеної хорди, утворює
з площиною основи кут
.Відрізок,
який сполучає центр верхньої основи
з серединою проведеної хорди, утворює
з площиною основи кут
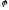 .Визначте
бічну поверхню циліндра.
.Визначте
бічну поверхню циліндра. .
Площа
бічної поверхні циліндра дорівнює
Q.
Знайдіть
площу перерізу, проведеного через
дану хорду паралельно осі циліндра.
.
Площа
бічної поверхні циліндра дорівнює
Q.
Знайдіть
площу перерізу, проведеного через
дану хорду паралельно осі циліндра.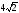 смвід
центра кулі проведено переріз кулі,
площа якого в 9 разів менша площі
великого круга. Знайдіть площу великого
круга.
смвід
центра кулі проведено переріз кулі,
площа якого в 9 разів менша площі
великого круга. Знайдіть площу великого
круга.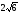 см.Знайдіть
площу перерізу.
см.Знайдіть
площу перерізу.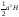 ;
в)а3Н?
;
в)а3Н?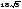 см3,,
а
її висота – 8 см. Знайдіть сторону
основи призми.
см3,,
а
її висота – 8 см. Знайдіть сторону
основи призми.