ЛЕКЦИЯ №41
14. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ
ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
14.1. Основные операторы и векторные операции
Электромагнитное поле – это вид материи, определяемый во всех точках двумя векторными величинами, которые характеризуют две его стороны, называемые электрическим полем и магнитным полем, и оказывающий силовое воздействие на заряженные частицы, зависящее от их скорости и заряда (ГОСТ 19880-74).
Основным математическим аппаратом при расчете электромагнитного поля является векторный анализ, включающий в себя понятия: скаляр, вектор и тензор. В общем случае скаляры и векторы являются функциями координат точки и времени. При анализе электромагнитного поля применяют линейный, поверхностный и объемный интегралы, а также дифференциальные операторы.
Оператор – это символ, характеризующий действие над вектором или скаляром, расположенным после символа.
Дифференциальные операторы позволяют сократить запись различных операций над скалярными и векторными величинами.
14.1.1. Линейный, поверхностный и объемный интегралы
Пусть имеется кривая l, ограничивающая поверхность S, которая находится в электромагнитном поле (рис. 14.1).
Линейный по кривой l интеграл является скалярной величиной
(14.1)
где
– вектор электромагнитного поля.
Вектор
имеет направление, касательное к элементу
кривой интегрирования l.
Циркуляцией
вектора
по замкнутой кривой l
называется интеграл вида:
. (14.2)
Поверхностный интеграл по поверхности S (рис. 14.2) имеет вид:
.
(14.3)
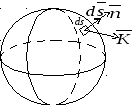
Рис. 14.2. К пояснению
поверхностного интеграла
Его
часто называют потоком вектора
через поверхность S.
Вектор
имеет направление, совпадающее с
направлением внешней нормали
к элементу замкнутой поверхности. Он
численно равен элементу поверхности
ds.
Объемный интеграл по объему V:
.
(14.4)
Элемент
объема
– это физически бесконечно малый объем,
который может иметь форму куба, сферы
и т.д.
14.1.2. Дифференциальные операторы набла и Лапласа
Оператор набла (оператор Гамильтона) – это символический вектор, сочетающий в себе векторные и дифференцирующие свойства. Поэтому при действии с оператором необходимо применять правила векторной алгебры.
В декартовой системе координат оператор записывается:
Существует запись его в цилиндрической и сферической системах координат.
При оперировании со сложными функциями используют правила дифференцирования сложных функций:
(14.5)
Использование оператора позволяет упростить запись некоторых векторных операций. Так умножение оператора на скалярную функцию означает градиент этой функции
. (14.6)
Скалярное умножение и вектора приводит к дивергенции вектора
. (14.7)
Векторное произведение на вектор дает ротор вектора
. (14.8)
Оператор
Лапласа
(лапласиан) – это скалярный дифференциальный
оператор, определяемый как дивергенция
градиента скалярной функции (уравнение
Лапласа
).
В
декартовой системе координат оператор
запишется:
(14.9)
Если
применить оператор
к вектору
,
то
(14.10)
где
Векторное
уравнение
можно представить тремя скалярными
уравнениями:
(14.11)
14.1.3. Понятие о градиенте, дивергенции и роторе
Градиент скалярной функции – это вектор, указывающий направление наиболее быстрого возрастания скалярной функции и по абсолютному значению равный наибольшей скорости возрастания этой функции.
(14.12)
Градиент направлен по нормали к поверхности равного уровня скалярной функции в данной точке. Градиент скалярного потенциала постоянного во времени поля равен:
(14.13)
где
– нормаль к эквипотенциальной поверхности
в данной точке поля.
Градиент
скалярного потенциала
в каждой точке совпадает с касательной
к силовой линии напряженности
электрического поля
в данной точке и имеет направление,
противоположное вектору
(рис.
14.3).
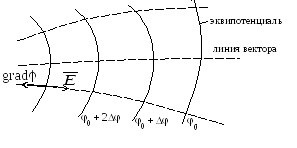
Рис. 14.3. Картина
электрического поля
Дивергенция (расхождение вектора) – это алгебраическая скалярная величина, характеризующая источники поля в рассматриваемой точке поля или указывающая на отсутствие источников
.
Численно дивергенцию в данной точке определяют как предел, к которому стремится отношение потока вектора через замкнутую поверхность к объему, ограниченному этой поверхностью, при стремлении этого объема к нулю
. (14.14)
Если
div
> 0, то имеются источники поля и линии
вектора
расходятся из данной точки. Точка
наблюдения служит началом (истоком)
линий вектора
.
Если
div
< 0, то в точке наблюдения линии вектора
сходятся, т.е. она служит стоком линий
вектора
.
Если
div
= 0, то в рассматриваемой точке отсутствует
источник линий вектора
.
Картина
электрического поля при наличии и
отсутствии зарядов показана на рис. 14.4.
Например, если имеется объемный
положительный заряд +,
то он является истоком вектора
электрического смещения
.
Рис. 14.4. Электрическое
поле при наличии и отсутствии электрических
зарядов
Дивергенция
вектора магнитной индукции
всегда равна нулю, так как линии вектора
замкнуты (не имеют начала и конца).
В декартовой системе координат
(14.15)
Ротор
(вихрь) вектора поля rot 
– это вектор, характеризующий интенсивность
вихревых полей в каждой точке. Ротор
проявляет себя как вихрь, поэтому он
имеет ось. Направление оси определяет
направление вектора, изображающего
ротор.
Численно
составляющую ротора в направлении
нормали
к плоской площадке s
определяют как предел, к которому
стремится отношение циркуляции вектора
к площадке s,
ограниченной контуром интегрирования,
при стремлении ее к нулю (рис. 14.5)
.
(14.16)
Если
вихревое поле в некоторой области не
имеет внутри источников векторных
линий, то rot
0 (div
= 0).
Запишем ротор вектора в декартовой системе координат
(14.17)
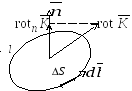
Рис. 14.5. К пояснению
определения ротора вектора
где: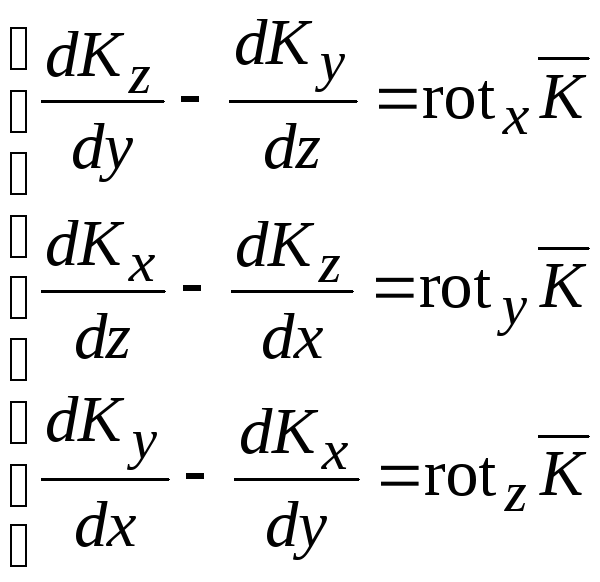 
.
(14.18)
(14.19)
14.1.4. Запись основных векторных операций с помощью оператора
Пространственные
производные grad, div и rot можно записать с
помощью оператора .
При этом умножение оператора
на скалярную функцию равносильно взятию
градиента этой функции
= grad .
Скалярное умножение оператора
и вектора дает дивергенцию этого вектора
,
а векторное их умножение образует ротор
вектора
.
Применение оператора
облегчает выполнение сложных векторных
операций. В табл.14.1 приведены примеры
символической записи наиболее часто
встречающихся векторных операций.