ЛЕКЦИЯ №36
13. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
13.1. Понятие об электрических цепях с распределенными параметрами
Строго говоря, всегда параметры электрической цепи в той или иной степени распределены вдоль ее участков, и только абстрагируясь от действительности можно предполагать, что такие параметры цепи как активное сопротивление – R, индуктивность – L и емкость – C сосредоточены в ее определенных участках. Во многих случаях такое допущение не приводит к существенным ошибкам в результатах проводимого анализа. Ранее мы имели дело с цепями с сосредоточенными параметрами. Однако, такой подход не всегда возможен. Например, рассматривая электромагнитные процессы, происходящие в электрических линиях, при помощи которых электрическая энергия или сигналы передаются на расстояние, необходимо иметь ввиду, что электрические и магнитные поля распределены по всей длине линии, и превращение электрической энергии в тепло также происходит по всей длине линии. Критерием необходимости рассматривать цепь в качестве цепи с распределенными параметрами является то, что интервал времени распространения электромагнитной волны вдоль всей цепи и интервал времени, в течение которого токи и напряжения меняются на заметную величину, должны быть соизмеримыми.
Токи напряжения в таких цепях являются функциями двух независимых переменных: времени – t и расстояния – x, отсчитываемого вдоль направления цепи. Уравнения, описывающие процессы в таких цепях, являются уравнениями в частных производных. Примерами являются линии передачи электрической энергии, линии связи, антенные вводы радиотехнических устройств, обмотки электрических машин при воздействии на них импульсных токов и напряжений.
Параметры цепи могут быть распределены неравномерно вдоль линии.
Однако во многих случаях этим можно пренебречь и считать параметры равномерно распределенными. Такие линии называются однородными.
В дальнейшем под величинами R, L, C, G, M будем понимать активное сопротивление, индуктивность и т.д., приходящиеся на единицу длины, и будем обозначать их через R0, L0, C0, G0, M0. В общем случае эти параметры зависят от частоты, например, увеличение активного сопротивления и индуктивности с ростом частоты вследствие поверхностного эффекта. Однако для простоты в дальнейшем это учитывать не будем.
13.2. Уравнения линии с распределенными параметрами
Напряжения и ток в линии являются функциями двух независимых переменных – пространственной координаты x, определяющей место наблюдения, и времени t, определяющей момент наблюдения. Считается, что направление координаты x совпадает с осью линии.
Необходимо найти пространственно-временное распределение величины тока в линии i(x, t) и напряжения между проводами u(x, t). В этом случае также можно определить процесс передачи энергии по линии, когда приемники и источники находятся на обоих концах линии.
Приняв положительное направление тока в линии слева направо, условимся называть "началом" левый конец линии. Расстояние от начальной точки до произвольной обозначим через x, а от конца – через x'. Вся длина линии l = x + x'.
Выделим элементарный участок x на расстоянии x от начала. Пользуясь первичными параметрами R0, L0, C0, G0, отнесенными к единице длины линии, представим приближенно участок x в виде схемы замещения (рис. 13.1).
Обозначим:
u – напряжение между верхним и нижним проводом в точке x;
u – приращение напряжения на участке x;
i – ток в точке x;
i – приращение тока на участке x.
Уравнения для приращений напряжения и тока на элементе x линии запишутся:
(13.1)
Это
уравнение в частных производных. По
мере стремления x
к нулю степень точности этих уравнений
повышается, причем величина второго
порядка малости
в правой части второго уравнения может
быть опущена.
В этом случае длинная линия рассматривается как цепная схема с бесконечно большим количеством звеньев, электрические параметры которых бесконечно малы.
Разделив обе части уравнений на x и перейдя к пределу x 0, получим дифференциальные уравнения линии
(13.2)
Эти уравнения носят название телеграфных.
Если за начало отсчета принять конец линии, т.е. ввести координату x', уравнения примут вид:
(13.3)
Уравнения (13.2) и (13.3) решаются однозначно при использовании начальных и граничных условий. Начальными условиями будут служить значения напряжения и тока в начале и конце линии в момент времени, принятый за нуль. Граничные условия определяются связями между напряжением и током в начале или в конце линии и зависят от заданного режима работы линии.
13.3. Периодический режим в однородной линии
При периодическом режиме под действием приложенного гармонического напряжения в любой точке линии напряжение и ток изменяются гармонически с частотой источника.
Обозначим комплексные действующие значения напряжения и тока на расстоянии x от начала линии через U = U(x) и I = I(x)
(13.4)
Так как комплексные величины U и I не зависят от времени t и являются только функциями расстояния x, то в уравнении (13.4) частные производные заменены обыкновенными.
Продифференцировав систему (13.4) по расстоянию x, получим отдельные уравнения относительно тока и напряжения
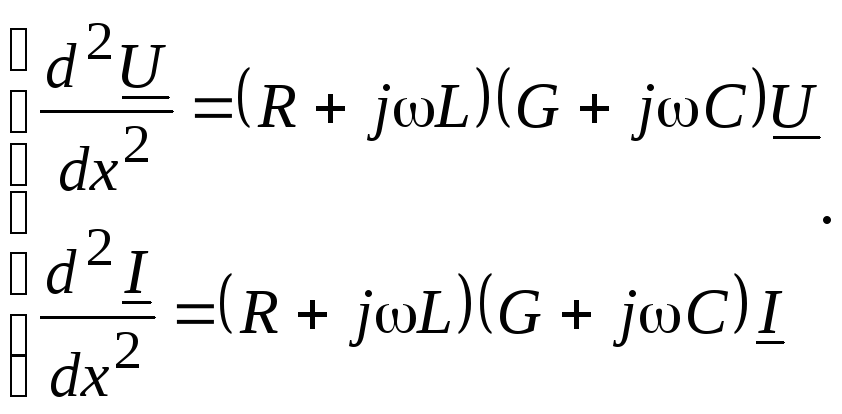(13.5)
Введем обозначение
(13.6)
Величина называется коэффициентом распространения волны. Тогда
(13.7)
В результате получили однородные линейные дифференциальные уравнения второго порядка одного вида.
Решение первого из них имеет вид:
(13.8)
Ток I проще всего находится подстановкой последнего уравнения в первое уравнение системы (13.4).
или
,
(13.9)
где
(13.10)
носит название волнового сопротивления линии.
(13.11)
Мгновенное значение напряжения в точке
x равно мнимой части
выражения
.
(13.12)
где 1 и 2 – аргументы комплексных чисел A1 и A2.
Таким образом, мгновенное значение напряжения в любой точке имеет две составляющие.
Рассмотрим первую из них.
Если считать точку x фиксированной и рассматривать изменение напряжения в данной точке в зависимости от времени, то первая составляющая в выражении (13.12) представляет собой гармоническую функцию с постоянной амплитудой.
Если
же считать момент t
фиксированным и рассматривать изменение
мгновенного напряжения вдоль линии
(т.е. в зависимости от расстояния x),
то получим затухающую гармоническую
волну напряжения, амплитуда которой
убывает с ростом х,
т.е. по мере удаления от начала линии.
Величина , характеризующая изменение амплитуды волны на единицу длины линии, называется коэффициентом затухания, а величина , характеризующая изменение фазы на единицу длины линии, называется коэффициентом фазы.
Убывание амплитуды волны вдоль линии обусловлено потерями в линии, а изменение фазы – конечной скоростью распространения электромагнитных колебаний.
На рис. 13.2 изображены волны напряжения, соответствующие двум следующим друг за другом моментами времени t1 и t2.
Расстояние между двумя ближайшими точками, взятое в направлении распространения волны, фазы колебаний напряжения различаются на 2, называется длиной волны –
,
. (13.13)
С течением времени волна перемещается от начала линии к ее концу. Она называется прямой или падающей волной.
