302_toe / ТОЭ 3 / Лекция №46

8

ЛЕКЦИЯ №46

15.10. Расчет электростатического поля с помощью уравнений

Лапласа и Пуассона

15.10.1. Расчет поля плоского конденсатора

Рассмотри плоский конденсатор (рис. 15.17а). Расстояние между пластинами конденсатора – d. К обкладкам приложено напряжение – U. Свободные заряды между пластинами отсутствуют. Требуется рассчитать поле между пластинами.

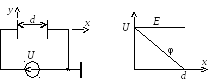
а) б)

Рис. 15.17. Поле плоского конденсатора при отсутствии зарядов

Поле при отсутствии в расчетной области свободных зарядов подчиняется уравнению Лапласа: .

В общем случае это уравнение записывается

Если предположить, что в направлении осей y и z поле не меняется, то уравнение упрощается:

После интегрирования получаем

Постоянные интегрирования находятся из граничных условий.

Без нарушения картины распределения поля можно принять потенциал одной из пластин, равным нулю. Тогда потенциал другой будет равен приложенному напряжению. При x = 0 потенциал  = U; а при x = d –  = 0:

;

;

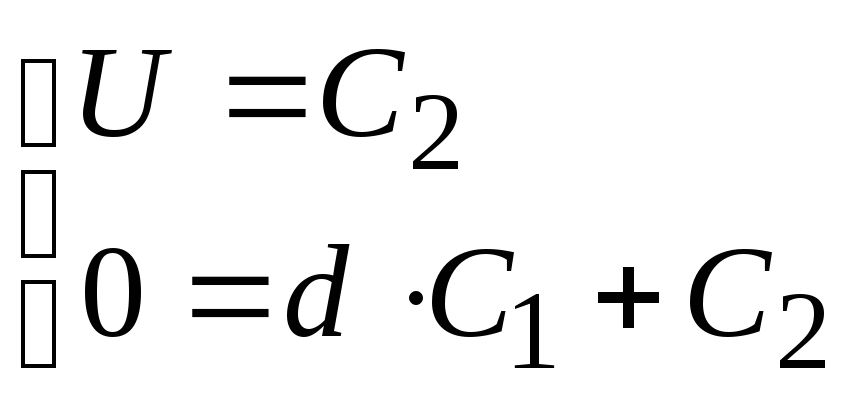. (15.44)

Следовательно, между пластинами потенциал линейно уменьшается от величины U до нуля (рис. 15.17б).

Напряженность поля

(15.45)

Напряженность поля не зависит от координаты x и численно равна U/d.

15.10.2. Расчет поля плоского конденсатора при наличии

свободных зарядов

Рассмотрим поле конденсатора, когда между пластинами имеются свободные заряды плотностью  (рис. 15.18).

Поле между пластинами подчиняется уравнению Пуассона

Рис. 15.18. К расчету поля конденсатора при наличии

свободных зарядов между пластинами

Допустим, что поле по осям y и z не изменяется. Тогда

(15.46)

После интегрирования получим

Общее решение уравнения (15.46)

(15.47)

Граничные условия в этом случае те же, что и в предыдущей задаче.

При x = 0 потенциал  = U, а при x = d –  = 0:

;

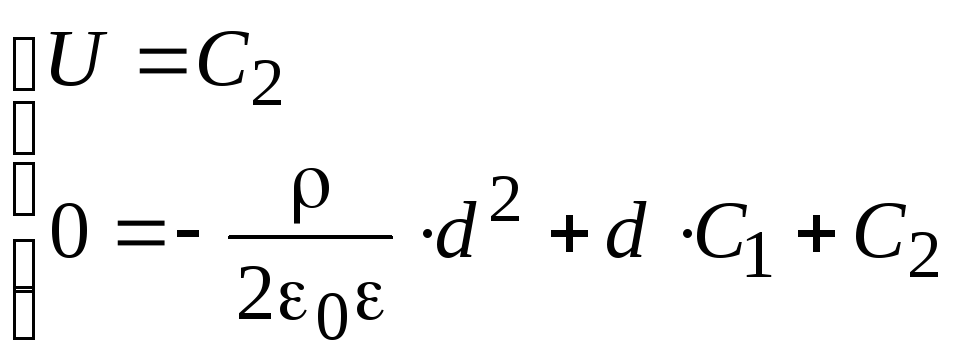Потенциал изменяется по закону

(15.48)

Напряженность поля

Модуль напряженности

(15.49)

Напряженность поля при наличии свободных зарядов не постоянна. Она прямо пропорциональна расстоянию от начала отсчета по оси x.

15.10.3. Влияние диэлектрического цилиндра на форму поля

Ц

Рис. 15.19. Диэлектрический цилиндр в электрическом поле

илиндр радиуса r₀ с проницаемостью ₁ помещен во внешнее плоскопараллельное поле напряженностью E₀ (рис. 15.19). Вектор напряжен­ности направлен по нормали к оси цилиндра. Внешняя среда имеет проницаемость ₂.

Требуется рассчитать поле как внутри, так и вне цилиндра.

Для решения задачи будем использовать уравнение Лапласа, записанное в цилиндрической системе координат

(15.50)

Будем считать, что внешнее поле по оси z не изменяется. При этом

Так как рассматриваемая среда имеет две области с различной диэлектрической проницаемостью, то дифференциальное уравнение (15.50) решается отдельно для обеих сред.

Для поля внутри цилиндра

(15.51)

Для поля вне цилиндра

(15.52)

Найдем закон распределения напряженности поля.

Внутри цилиндра (r < r₀)

(15.53)

Следовательно, поле ориентировано по направлению внешнего поля.

При ₁ > ₂ E₁ < E₀, при ₁ < ₂ E₁ > E₀.

Таким образом, можно записать

Учитывая, что вектора и ориентированы одинаково

(15.54)

По модулю вектор напряженности поля, обусловленный поляризацией, меньше вектора напряженности внешнего поля. А направление его зависит от соотношения диэлектрических проницаемостей и .

За пределами цилиндра ()

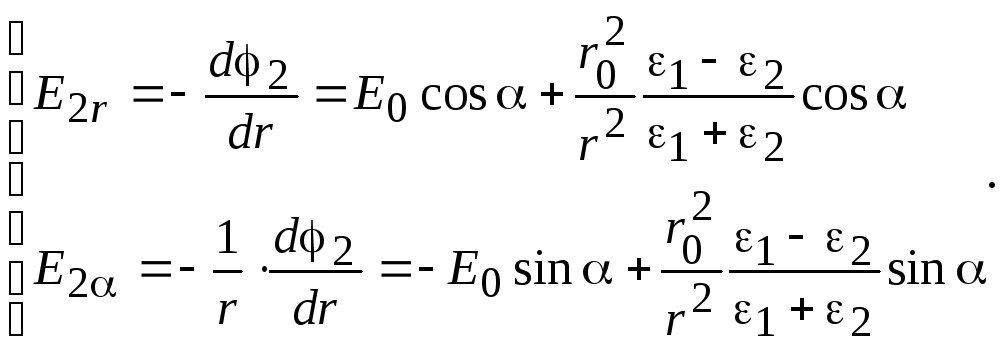(15.55)

В случае внесения в поле металлического цилиндра ()

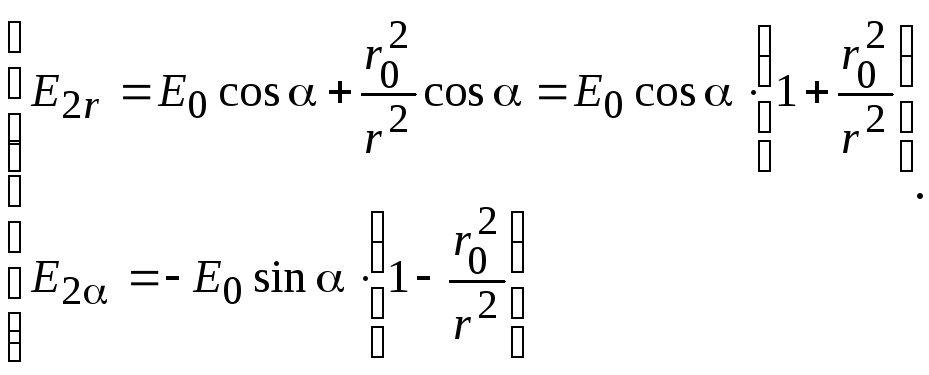(15.56)

15.11. Диэлектрическая вязкость

Вектор электрического смещения в общем виде записывается

(15.57)

В этом уравнении считается, что поляризация вещества происходит мгновенно, или же происходит медленное изменение магнитного поля, т.е. рассматривается квазистатическое поле.

Рассмотрим, как происходит поляризация в реальных условиях.

В гидродинамике вязкость записывается

Первое слагаемое показывает статическое значение поляризации, а второе – поляризацию в данный момент времени.

С учетом 1 +  =  уравнение (15.56) можно переписать в виде

Допустим, что поле изменяется синусоидальному закону. В этом случае целесообразно прейти к комплексной форме записи.

(15.58)

где – комплексная диэлектрическая восприимчивость, тогда

(15.59)

Это уравнение полностью аналогично уравнению (15.10).

Комплексная диэлектрическая проницаемость

(15.60)

Если избавиться от иррациональности в знаменателе, то

Таким образом, введение понятия вязкости привело к зависимости диэлектрической проницаемости от частоты.

При

(15.61)

т.е. на низких частотах вязкие свойства отсутствуют, и поляризация происходит мгновенно.

При

(15.62)

Следовательно, на высоких частотах  = 1, т.е. среда обладает свойствами вакуума, и поляризация не происходит, так как молекулы не успевают подстраиваться к полю.

16. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ПОСТОЯННОГО ТОКА

В ПРОВОДЯЩЕЙ СРЕДЕ

16.1. Плотность тока и ток

Если под воздействием внешних источников в проводящей среде создано электрическое поле, то в ней будет протекать электрический ток. Свойство среды, характеризующее ее способность проводить ток, называется удельной проводимостью. Она зависит от физических свойств проводящего материала и температуры, измеряется в См/м.

Основной величиной в электрическом поле проводящей среды является плотность тока . Это векторная величина, направленная по напряженности электрического поля.

Ток определяют как поток вектора плотности тока

(16.1)

Ток является скалярной алгебраической величиной.

При протекании постоянных токов как внутри проводящих тел, так и вне их существуют постоянные магнитные поля. Так как эти поля неизменны во времени, то в поле явление электромагнитной индукции отсутствует. Поэтому электрическое и магнитное поле постоянного тока можно рассматривать раздельно. Магнитные поля постоянного тока будут рассмотрены в следующей главе.

16.2. Закон Ома, I, II законы Кирхгофа в дифференциальной форме

Выделим в проводящей среде небольшой параллелепипед объемом V (рис. 16.1).

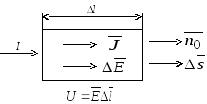
Рис. 16.1. Параллелепипед в проводящей среде

Длина ребер параллелепипеда l, площадь поперечного сечения s.

Расположим его так, чтобы напряженность поля была в нем направлена параллельно ребру. В силу малости объема можно считать, что напряженность поля одна и та же во всем элементарном объеме:

где – единичный вектор по направлению _.

Ток:

(16.2)

Напряжение на элементе объема:

(16.3)

Сопротивление элемента объема:

, (16.4)

где  – удельная проводимость среды.

Поставив в (16.3) выражения (16.2) и (16.4) получим:

,

. (16.5)

Выражение (16.5) называют законом Ома в дифференциальной форме. Это уравнение справедливо для областей вне источников ЭДС. В областях, занятых источниками ЭДС, существует также так называемое стороннее электрическое поле, обеспечивающее непрерывное движение зарядов в электрической цепи. Это поле обусловлено химическими, электрохимическими, тепловыми и термоэлектрическими процессами. Закон Ома в дифференциальной форме для областей, занятых источниками ЭДС

(16.6)

Уравнение (16.6) называется обобщенным законом Ома. Если от обеих частей взять интеграл по замкнутому контуру, то получим второй закон Кирхгофа в дифференциальной форме.

Если в проводящей среде выделить некоторый объем, по которому протекает постоянный, не изменяющийся во времени ток, то можно сказать, что ток, входящий в объем, равняется току, выходящему из объема, иначе в этом объеме происходило бы накопление электрических зарядов, что опыт не подтверждает. Математически это записывают так:

(16.7)

Разделим правую и левую часть уравнения (16.7) на объем и возьмем предел в случае, когда объем стремится к нулю

(16.8)

Соотношение (16.8) называется первым законом Кирхгофа в дифференциальной форме. Он гласит, что в установившемся режиме (при постоянном токе) в любой точке тока нет ни истока, ни стока линий тока проводимости .