302_toe / ТОЭ 3 / Лекция №37

6

ЛЕКЦИЯ №37

Скорость перемещения падающей волны вдоль линии называется фазовой скоростью. Она определяется как скорость перемещения точки, фаза колебаний которой остается постоянной. Для прямой волны это условие записывается в виде

Следовательно:

(13.14)

Аналогичное исследование второго слагаемого выражения (13.12) показывает, что для произвольного момента времени она представляет синусоидальную волну, амплитуда которой возрастает с увеличением х, т.е. по мере удаления от начала линии к ее концу. С течением времени волна перемещается от конца линии к ее началу. Эта волна называется обратной или отраженной волной (рис. 13.3). Фазовая скорость обратной волны .

Мгновенное напряжение можно рассматривать как сумму двух волн, движущихся в противоположных направлениях, причем каждая из этих волн затухает в направлении движения

. (13.15)

За время, равное одному периоду, обе волны перемещаются на расстояние, равное длине волны.

Линии, физическая длина которых соизмерима с длиной волны, считаются длинными линиями. При достаточно высоких частотах практически любая протяженная электрическая цепь становится «длинной» по отношению к длине волны.

Например, фазовая скорость в воздушной линии близка к скорости света (310⁸ м/с) и при частоте 50 Гц длина волны составляет 6000 км, а при частоте 310⁹ Гц – 10 см.

Запишем прямую и обратную волны в комплексной форме

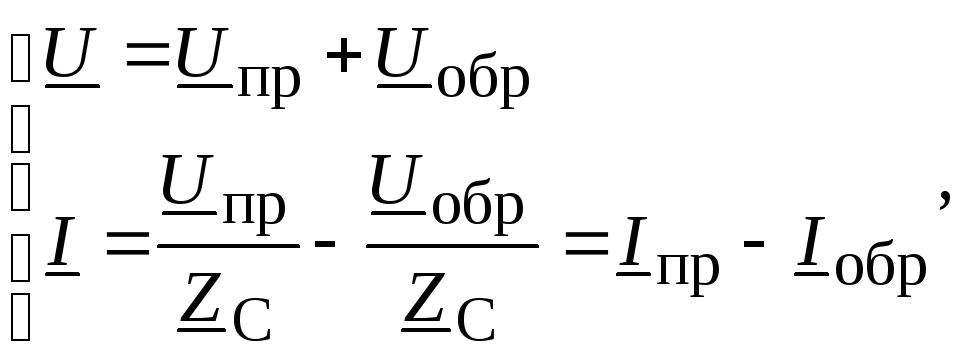(13.16)

где

Напряжение и ток прямой и обратной волн связаны законом Ома

Постоянные интегрирования A₁ и A₂ находятся в зависимости от напряжения и тока в начале линии (граничные условия), если они заданы.

При х = 0

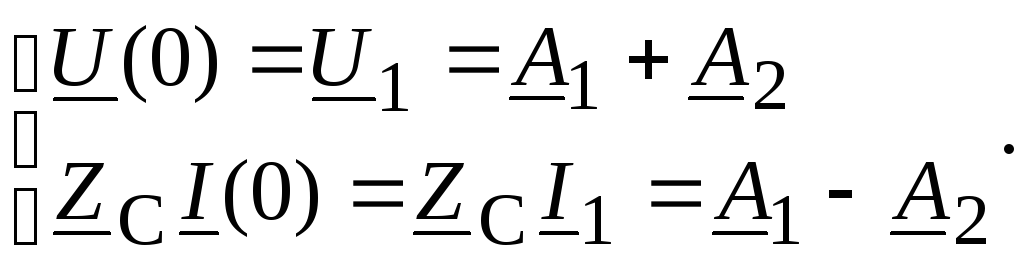
Откуда

13.4. Уравнения линии в гиперболических функциях

Подставив значения постоянных интегрирования в уравнения для напряжения и тока получим:

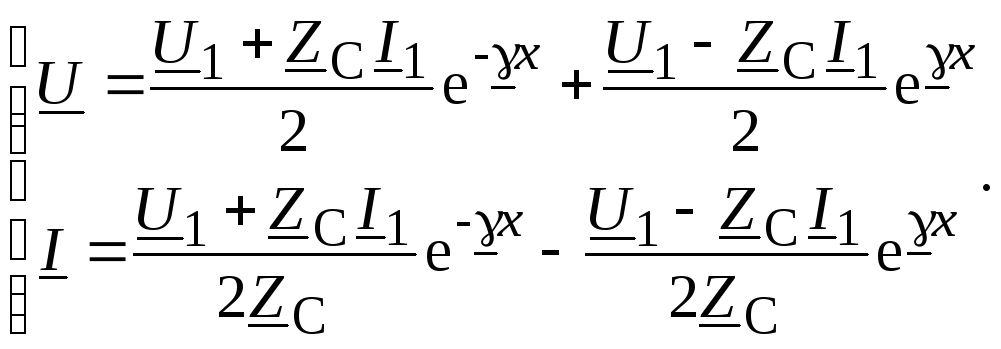(13.17)

Сгруппируем члены, включающие ток и напряжение

.

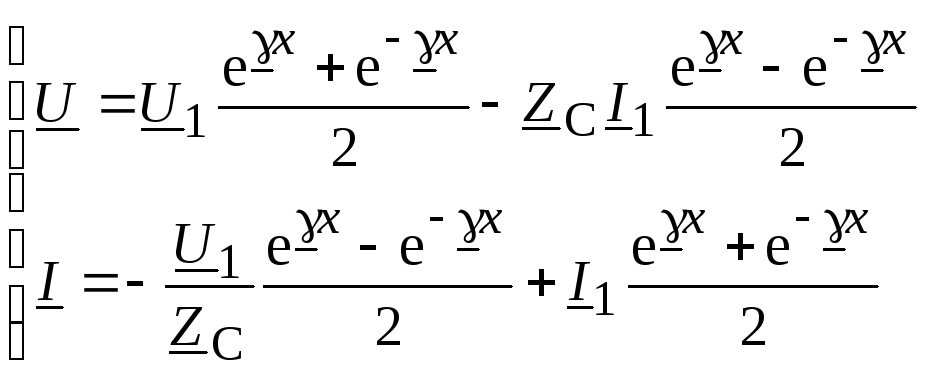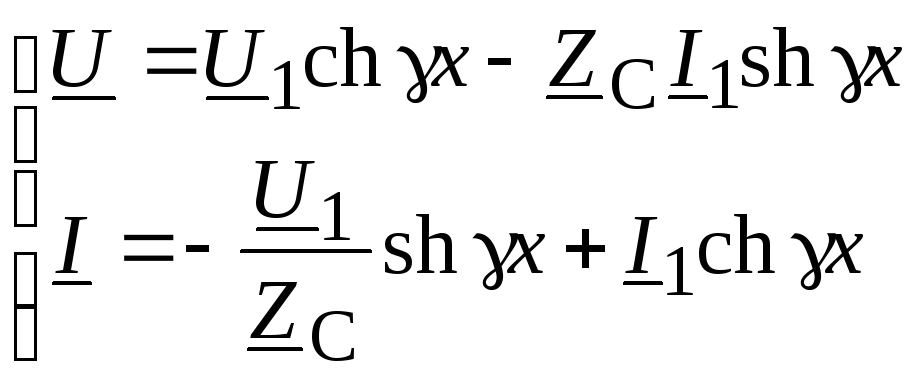. (13.18)

Эти уравнения не содержат в явном виде прямые и обратные волны, так как их составляющие кусочно вошли в гиперболические функции.

Если известны параметры нагрузки, то удобнее расстояние отсчитывать от конца линии x = l – x':

;

;

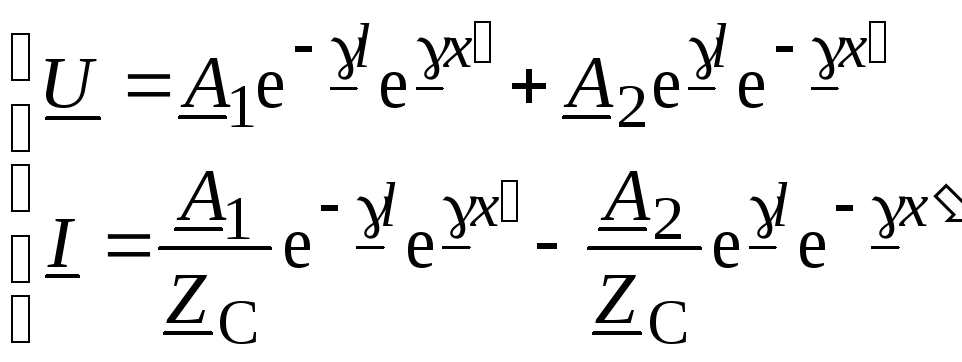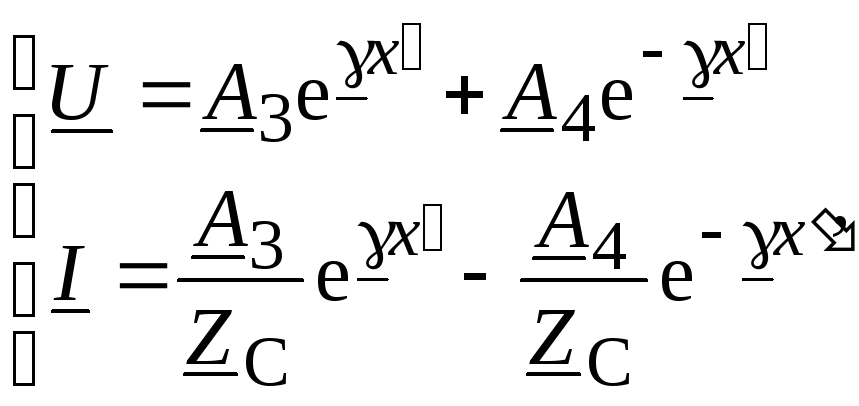(13.19)

где

Постоянные интегрирования и находятся в зависимости от напряжения и тока в конце линии (граничные условия), если они заданы.

При

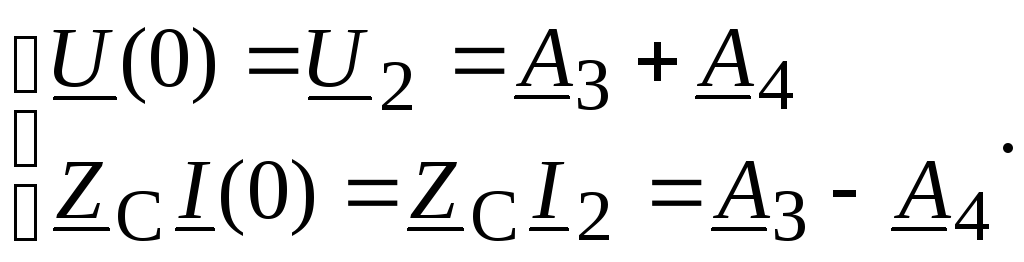
Откуда

Следовательно

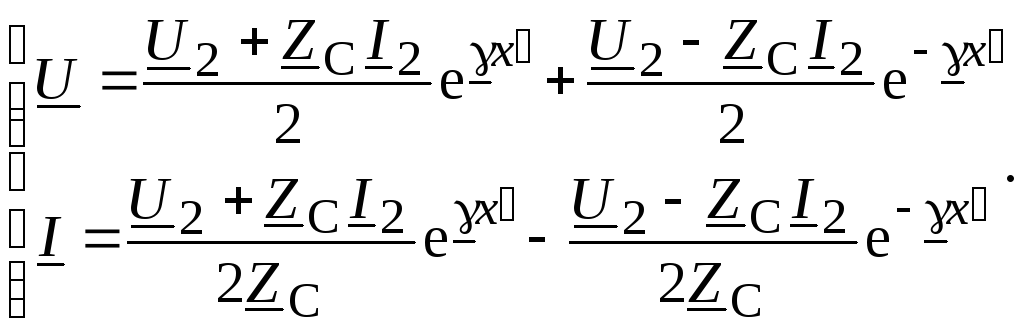(13.20)

Сгруппируем члены, включающие ток и напряжение

;

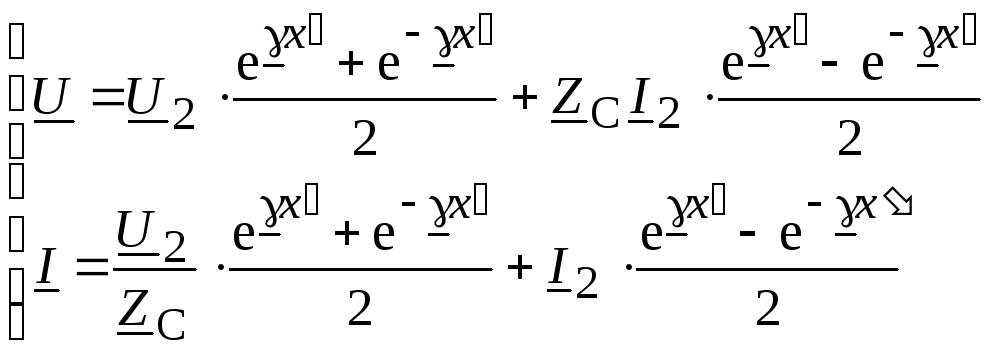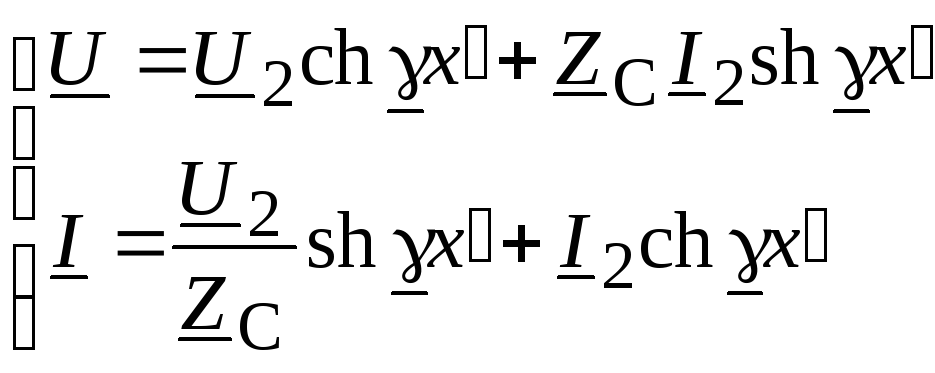. (13.21)

13.5. Вторичные параметры линии

Распределение тока и напряжения вдоль линии зависит от коэффициента распространения волны и волнового сопротивления, которые называются вторичными параметрами

где – продольное сопротивление, – поперечная проводимость.

Рассмотрим зависимость вторичных параметров от частоты.

При  = 0

т.е. коэффициент распространения и волновое сопротивление являются чисто активными величинами.

С ростом частоты коэффициент затухания и коэффициент фазы монотонно увеличиваются. Причем если перейти к пределу , то обнаружится, что коэффициент затухания стремится к величине

а коэффициент фазы асимптотически приближается к прямой .

Так как обычно в линиях , то волновое сопротивление с ростом частоты уменьшается, стремясь к пределу .

Зависимости вторичных параметров линии от частоты показаны на рис. 13.4.

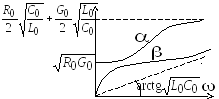
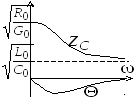
Рис. 13.4. Частотные характеристики вторичных параметров

Частотные характеристики говорят о том, что вследствие зависимости коэффициентов затухания и фазы от частоты сигнал сложной формы, проходя по линии, искажается.

Пример расчета вторичных параметров воздушной линии.