302_toe / ТОЭ 3 / Лекция №42

6

ЛЕКЦИЯ №42

14.1.5. Интегральные теоремы

Теоремы Остроградского-Гауса и Стокса применяют при переходе от уравнений поля, записанных в интегральной форме, к уравнениям поля в дифференциальной форме и наоборот.

Таблица 14.1

Векторная операция	Символическая запись с помощью оператора 	Примечание
1	2	3
grad 	
div	
rot		+=div +grad 
div 	()
div grad 	() = 2
div rot	() = 0	Исток вихревого поля всегда отсутствует
rot grad 	() = 0	Векторное поле, имеющее градиент скалярной функции, всегда безвихревое, т.е. потенциальное
rot div	() = 0	Векторное поле, имеющее дивергенцию векторной функции, всегда безвихревое
rot rot	()
rot 	()

Теорема Остроградского-Гауса устанавливает соотношение между интегралом дивергенции вектора по объему V и поверхностным интегралом, взятым по замкнутой поверхности s, ограничивающей этот объем

. (14.20)

При этом поверхность должна быть кусочно-гладкой, а вектор на этой поверхности – непрерывным. Положительной является внешняя нормаль.

Теорема Стокса приравнивает поверхностный интеграл ротора вектора к линейному интегралу этого вектора, взятого по замкнутому контуру l, ограничивающему эту поверхность

. (14.21)

Вектор должен быть непрерывным по всему контуру интегрирования, а контур – кусочно-гладким.

14.2. Понятие об электромагнитном поле.

Частные виды электромагнитного поля

На электромагнитное поле как на вид материи распространяются понятия, относящиеся к свойствам вещества: инертная, гравитационная масса и энергия, количество движения и момент количества движения. Наличие инертной массы электромагнитного поля подтверждается опытами великого русского ученого физика П.Н. Лебедева, обнаружившего световое давление на твердые тела (1899) и газы (1907). Инертная масса электромагнитного поля имеет ничтожную плотность.

Электромагнитное поле является носителем гравитационной массы, что подтверждается искривлением светового луча в поле тяготения Солнца, замеченным во время солнечного затмения 1919 г., а также тем, что энергия (скорость) луча увеличивается при движении вниз к земле и уменьшается при движении вверх от земли (опыт Ландау, 1960).

Электромагнитное поле обладает энергией, так как при взаимодействии с заряженными частицами их энергия изменяется и, следовательно, передается электромагнитному полю и наоборот.

Движение энергии электромагнитного поля количественно оценивается вектором Пойнтинга. В дальнейшем будем рассматривать макроскопическую теорию электромагнитного поля, которая не учитывает дискретного распределения электрических зарядов в веществе, считая вещественную среду сплошной. В этом случае для характеристики поля используют усредненные значения микроскопических величин в бесконечно малом объеме, введя четыре основные вектора .

Электромагнитное поле является совокупностью переменных взаимосвязанных и влияющих друг на друга электрического и магнитного полей. Частными видами электромагнитного поля являются:

1. Электростатическое поле, которое создается неподвижными заряженными телами и проявляется в виде механической силы, действующей на неподвижный электрический заряд. Это поле потенциально, т.е. rot = 0.

2. Электрическое поле постоянного тока (стационарное электрическое поле) образуется внутри и вне проводников при прохождении по ним постоянного тока. При этом внутри однородного проводника отсутствует объемная плотность заряда, т.е. div  = 0. Поле является потенциальным и для него справедливо уравнение Лапласа ² = 0.

3. Магнитное поле постоянного потока проявляется в силовом воздействии на движущиеся в нем заряженные тела и на неподвижные контуры с постоянным током. Поле имеет вихревой характер ().

Электрическое поле постоянного тока и магнитное поле постоянного потока могут рассматриваться независимо друг от друга.

14.3. Основные характеристики электромагнитного поля

1. Напряженность электрического поля – физическая характеристика электрического поля, определяющая силовое воздействие поля на электрический заряд.

Напряженность электрического поля является векторной величиной, численно равной отношению силы , с которой электрическое поле действует на положительный заряд Q, внесенный в рассматриваемую точку поля, к значению этого заряда, когда его величина стремится к нулю

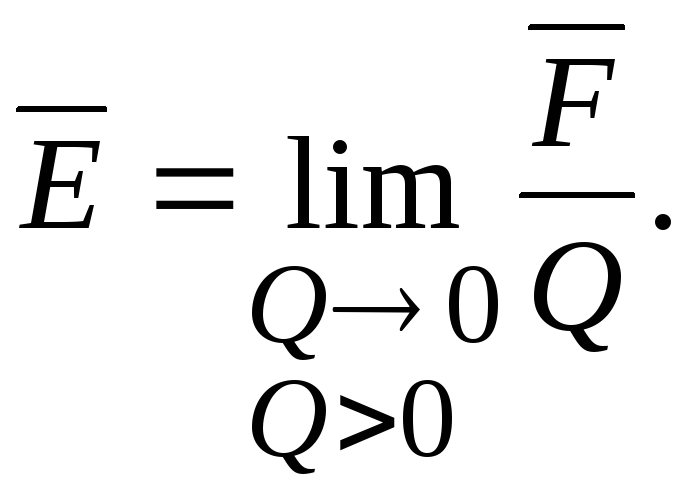(14.22)

За положительное направление вектора напряженности принято направление от положительного заряда + Q к отрицательному – Q (рис. 14.6).

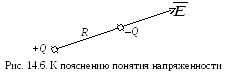
Сила электрического поля, действующая на заряд, направлена вдоль вектора . Линия напряженности электрического поля – это линия, в каждой точке которой вектор касателен к ней. Уравнение линии вектора напряженности электрического поля:

(14.23)

где dx, dy, dz – проекции элемента длины dl вектора .

Для любой точки поля напряженность и потенциал поля связаны выражением

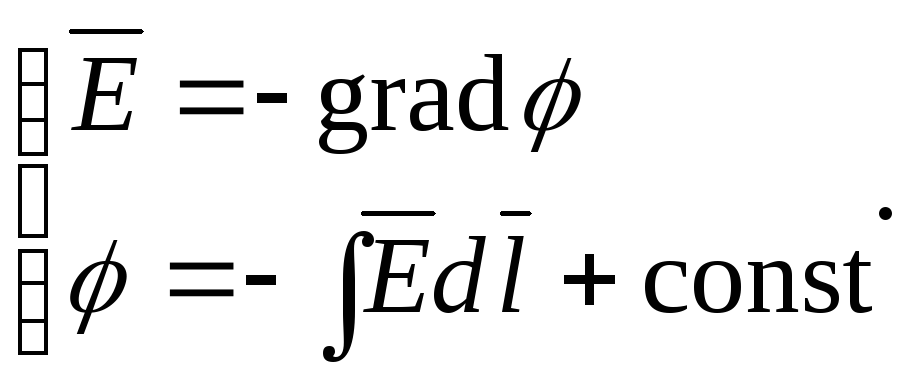(14.24)

Напряженность имеет электростатическое происхождение. Существует также напряженность _стор, которая создается сторонними электростатическими силами (индукционными, термоэлектрическими, контактными на поверхностях различных проводников и др.). В этом случае результирующая напряженность электрического поля тока:

(14.25)

2. Магнитная индукция – это физическая характеристика магнитного поля, определяющая силовое воздействие на движущийся заряд. Магнитная индукция – векторная величина, характеризующая магнитное поле в каждой его точке.

Численно магнитную индукцию поля можно определить по механической силе, действующей на один движущийся заряд, элемент объема с заданной плотностью тока в нем, либо на элемент проводника с током.

Для заряда Q, движущегося со скоростью v во внешнем поле:

(14.26)

Направление силы находят по правилу векторного произведения (). Механическая сила максимальна при , и равна нулю при .

Направление магнитной индукции можно определить по правилу буравчика (правого винта), если буравчик вращать от вектора силы к вектору скорости положительного заряда Q (рис. 14.7).

14.4. Виды плотности тока

Английский ученый Д.К. Максвелл ввел понятие тока смещения в вакууме, как изменение во времени вектора напряженности электрического поля в вакууме, плотность которого равна . Ток смещения в вакууме не возникает в результате движения электрических зарядов, но возбуждает магнитное поле по тем же законам, что и все виды токов.

Ток смещения в диэлектрике состоит из тока смещения в вакууме и тока поляризации, возникающего в результате движения связанных зарядов диэлектрика. Плотность тока смещения в диэлектрике

(14.27)

где  – диэлектрическая восприимчивость, характеризующая свойство диэлектрика поляризоваться.

Введение понятия тока смещения в диэлектрике позволило Максвеллу теоретически доказать, что энергия, излучаемая источником электромагнитного поля, должна распространяться по диэлектрику в виде электромагнитных волн. В 1887 г. немецкий ученый Г. Герц экспериментально доказал существование электромагнитных волн.

Существуют понятия о следующих плотностях тока.

1. Вектор плотности тока проводимости

(14.28)

образуется движением зарядов в проводящей среде под действием постоянного или переменного во времени поля напряженностью . Он сопровождается выделением тепла по закону Джоуля-Ленца. Линии вектора постоянного тока непрерывны (div = 0). Линии вектора переменного тока не замкнуты, поэтому

(14.29)

где  – объемная плотность заряда.

2. Вектор плотности тока переноса

(14.30)

образуется заряженными телами и частицами, движущимися в непроводящей среде или в вакууме со скоростью .

3. Вектор плотности тока поляризации

(14.31)

возникает в переменном во времени поле напряженностью в результате смещения связанных зарядов молекул диэлектрика. Тепловые потери не подчиняются закону Джоуля-Ленца.

4. Вектор тока смещения в вакууме

(14.32)

существует в вакууме только в переменном во времени поле. Он не вызывает выделения теплоты по закону Джоуля-Ленца.

5. Вектор плотности тока смещения в диэлектрике

(14.32)

наблюдается в диэлектрике только в переменном во времени поле. Может происходить выделение теплоты, но не по закону Джоуля-Ленца. На поверхности проводника .

6. Вектор плотности полного тока

при (14.34)

Линии плотности полного тока всегда замкнуты

(14.35)

Общим свойством для всех видов тока является создание магнитного поля, описываемого уравнением Максвелла

(14.36)