
Лабораторный Практикум по Дискрмат2
.pdf
Образец выполнения заданий
1. Доказать равносильность данных формул логики предикатов
а) |
x P x |
Q x |
xP x |
|
xQ x 1 ; |
|
|
|
|
|
|
б) |
x P x |
Q x |
x P(x) Q x 0 . |
||
2. Проверить правильность логического следствия. |
|||||
в) |
x P x |
Q x | |
xP x |
|
xQ x . |
Решение. |
а) Для доказательства равносильности формулы единице, |
||||
достаточно доказать ее тождественную истинность. Докажем от обратного. Предположим, что данная формула F не является тождественно истинной, а является опровержимой. То есть, существуют такие конкретные предикаты P и Q, при подстановке которых в формулу F эта формула становится ложным высказыванием. Тогда, по определению импликации,
высказывание |
F1 |
x P x |
Q x |
будет истинным высказыванием, а |
||
F2 |
xP x |
xQ x – |
ложным |
высказыванием. По определению |
||
квантора общности |
высказывание |
F1 |
истинно только тогда, когда |
|||
P x |
Q x – |
тождественно истинный |
предикат. При помощи закона |
|||
Моргана для кванторов запишем формулу F2 в следующем виде:
F2 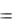 xP(x)
xP(x)  xQ x
xQ x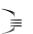 xP(x)
xP(x)  xQ x .
xQ x .
Тогда из ложности высказывания F2, по определению дизъюнкции,
|
|
|
|
|
|
|
|
|
следует |
ложность высказывания |
xP (x) . Тогда P (x) – тождественно |
||||||
ложный |
предикат, а P(x) |
– тождественно истинный. Из ложности |
||||||
высказывания xQ x , следует опровержимость предиката Q x . |
Но если |
|||||||
P x – тождественной истинный, а Q x - опровержимый, то P x |
Q x |
|||||||
будет опровержимым предикатом. Из истинности высказывания F1 |
||||||||
следует, |
что предикат P x |
Q x |
– тождественно истинный. Получили |
|||||
противоречивые утверждения. Из противоречивости этих утверждений следует ложность предположения. Следовательно, данная формула тождественно истинная.
б). Для доказательства равносильности данной формулы нулю достаточно доказать ее тождественную ложность. Предположим обратное, что данная формула не является тождественно ложной, а является выполнимой. То есть, для некоторых конкретных предикатов P и Q данная формула будет истинным высказыванием. Тогда по определению
61

конъюнкции истинными будут также высказывания x P x |
|
Q x |
и |
|||||
|
|
|
|
|
|
|
|
|
x P(x) |
Q x . |
Откуда, по определению действия кванторов, |
предикат |
|||||
|
|
будет |
тождественно истинным предикатом, P(x) |
|
|
|
– |
|
P x Q x |
|
Q x |
||||||
выполнимым предикатом, а P(x) Q x будет опровержимым предикатом.
будет опровержимым предикатом.
При |
помощи |
|
равносильных преобразований получим, что предикат |
|||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
P(x) |
Q x |
P (x) Q(x) P(x) Q(x) – опровержимый предикат, что |
|||||
противоречит полученному ранее выводу о тождественной истинности этого предиката. Из противоречивости выводов следует ложность предположения. Следовательно, данная формула тождественно ложна.
в) По определению логического следствия, для любых конкретных предикатов P и Q в случаях истинности посылки заключение также должно быть истинным. Тогда следствие будет верным. Предположим обратное: пусть для некоторых P и Q посылка истинна, а заключение
ложное. Из истинности гипотезы следует, что P x |
Q x – тождественно |
|||||||||||||||||||||||||
истинный |
|
предикат. |
|
|
В |
|
|
|
|
силу |
|
|
того, |
|
|
|
|
что |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
P x |
Q x |
(P x Q x ) |
(Q x |
P x , |
тождественно |
|
истинными |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
будут |
также |
предикаты P x |
|
Q x |
и Q x |
P x , а их отрицания - |
||||||||||||||||||||
тождественно |
|
ложными. |
Кроме |
|
того, |
ложность |
заключения |
|||||||||||||||||||
xP x |
xQ x означает, что высказывание |
xP x |
истинное, а |
xQ x |
||||||||||||||||||||||
– ложное высказывание. Либо, что высказывание |
xP x |
– |
|
ложное, а |
||||||||||||||||||||||
xQ x |
– истинное высказывание. В первом случае предикат P x |
будет |
||||||||||||||||||||||||
тождественно истинным, а Q x |
|
|
|
|
|
|
|
|
||||||||||||||||||
– опровержимым и, следовательно, Q x – |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
выполнимым предикатом. Тогда P(x) |
Q x – выполнимый предикат, что |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
противоречит тождественной ложности отрицания предиката P (x) |
Q x . |
|||||||||||||||||||||||||
Во втором случае предикат P(x) |
будет |
опровержимым, |
|
Q x |
|
– |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
тождественно истинным, а P (x) – выполнимым. Тогда P (x) |
|
Q x |
будет |
|||||||||||||||||||||||
выполнимым предикатом, что противоречит тождественной ложности отрицания предиката Q (x) P x . Таким образом, в обоих случая
получаем противоречивые утверждения. Следовательно, обратное предположение ложное, а истинно исходное утверждение. Вывод: данное логическое следствие верное.
Вопросы для самопроверки
1.Определите основные классы предикатов.
2.Определите основные классы формул логики предикатов.
3.Как связаны основные тавтологии алгебры высказываний и логики предикатов?
4.Перечислите основные свойства кванторных операций.
62

5. Определите понятие логического следствия формул логики предикатов.
Литература: [3], гл. 3, с. 56–74; [2], Часть 4, с. 68–80; [7], гл. 3, стр. 80–88. [12], §7, стр. 96–117.
Вариант 1.
а) б) в)
Вариант 2.
а)
б)
в)
Вариант 3.
а) б)
в)
Вариант 4.
а) б)
в)
Вариант 5.
а)
б) в)
Вариант 6.
а)
б)
в)
Задания для самостоятельной работы
x P x Q x |
x P x |
Q x 1; |
||
|
|
|
|
|
x P x Q x |
x P(x) |
Q x 0 ; |
||
x P x Q x | |
xP x |
xQ x . |
||
x P x Q x |
x P x |
Q x 1; |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x P x Q x |
x P(x) |
Q x 0 ; |
|
|||||||||||
x P x |
Q x , |
xP x | |
xP x |
xQ x . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
x P x Q x |
x P x |
|
Q x 1; |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
x P x |
Q x |
x P(x) |
|
Q x 0 ; |
||||||||||
xP x |
xQ x | |
|
|
|
x P x Q x . |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
x P x Q x |
x P x |
|
Q x 1; |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
x P x |
Q x |
x P(x) |
|
Q x 0 ; |
||||||||||
x P x |
Q x | |
|
|
xP x |
|
xQ x . |
|
|||||||
x P x Q x |
x P x Q x 1; |
|||||||||||||
|
|
|
|
|
|
|
||||||||
x P x Q x |
x P(x) Q x 0; |
|
||||||||||||
xP x |
xQ x | |
|
|
|
x P x |
|
Q x . |
|
||||||
x P x Q x |
x P x Q x 1; |
|||||
|
|
|
|
|
|
|
x P x Q x |
x P(x) Q x 0 ; |
|||||
xP x |
xQ x | |
|
x P x Q x . |
|||
63
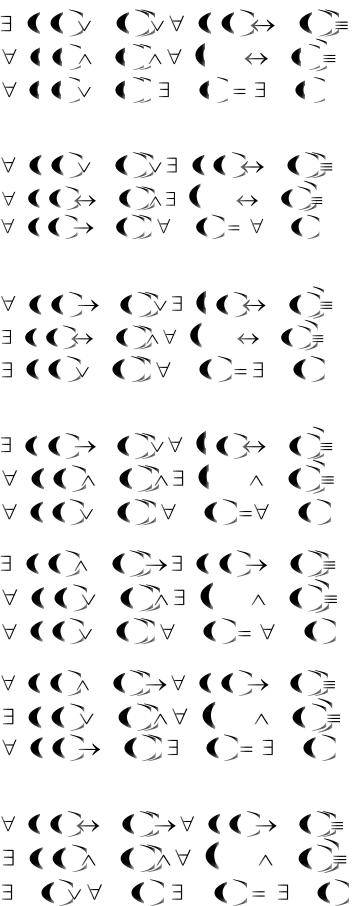
Вариант 7.
а)
б)
в)
Вариант 8.
а)
б) в)
Вариант 9.
а)
б)
в)
Вариант 10. а)
б)
в) Вариант 11.
а)
б)
в) Вариант 12.
а)
б) в)
Вариант 13. а)
б)
в) Вариант 14.
x P x Q x |
|
|
x P x |
|
|
Q x 1; |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x P x Q x |
|
x P(x) |
|
Q x 0 ; |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x P x Q x , |
xP x | |
xQ x . |
||||||||||||||||||||||||||||
x P x Q x |
x P x |
Q x 1; |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x P x |
Q x |
x P(x) |
Q x 0 ; |
|||||||||||||||||||||||||||
x P x |
Q x , |
xP x | |
xQ x . |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x Q x |
P x |
|
|
x P x |
Q x 1; |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x P x |
Q x |
x P(x) |
Q x 0 ; |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x P x Q x , |
xP x | |
xQ x . |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x Q x |
P x |
|
|
x P x |
Q x 1; |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x P x Q x |
|
|
x P(x) Q x 0; |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x P x Q x , |
xP x | |
xQ x . |
||||||||||||||||||||||||||||
x P x Q x |
|
|
x Q x |
|
P x 1; |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x P x Q x |
|
|
|
x P(x) Q x 0; |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
x P x Q x , |
xP x | |
|
|
xQ x . |
||||||||||||||||||||||||||
x P x Q x |
|
|
x Q x |
|
|
P x 1; |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
x P x Q x |
|
|
|
x P(x) Q x 0; |
||||||||||||||||||||||||||
x P x |
Q x , |
xP x | |
|
|
xQ x . |
|||||||||||||||||||||||||
x P x |
Q x |
|
|
|
|
|
x P x Q x 1; |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
x P x Q x |
|
|
|
x P(x) Q x 0 ; |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
xP x |
xQ x , |
|
|
xQ x | |
|
|
xP x . |
|||||||||||||||||||||||
64
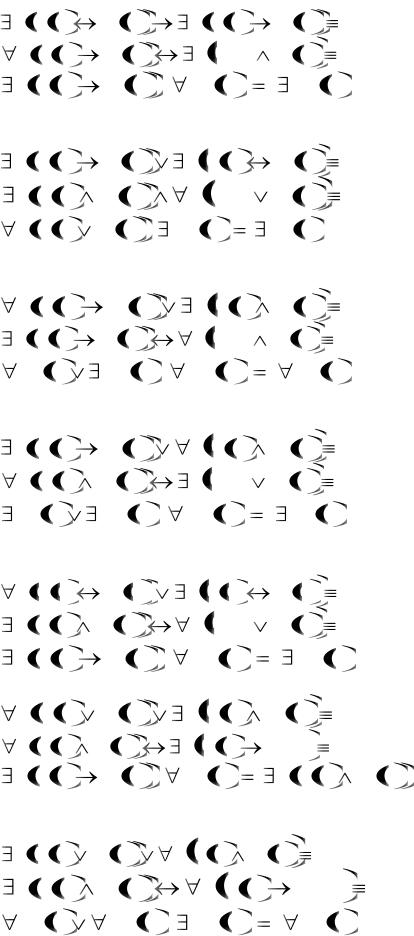
а)
б) в)
Вариант 15. а)
б)
в)
Вариант 16. а)
б)
в)
Вариант 17. а)
б)
в)
Вариант 18. а)
б)
в) Вариант 19.
а) б) в)
Вариант 20.
а)
б)
в)
x P x |
Q x |
|
x P x Q x 1; |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x P x Q x |
|
|
x P(x) Q x 0 ; |
|||||||||||||||||||||||||||||||
x P x |
Q x , |
|
xP x | |
|
|
|
|
xQ x . |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x Q x |
P x |
|
x P x |
|
|
Q x 1; |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x P x Q x |
|
x P(x) Q x 0; |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x P x Q x , |
xQ x | |
xP x . |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x P x |
Q x |
|
|
x P x Q x 1; |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x P x Q x |
|
|
x P(x) Q x 0; |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
xP x |
xQ x , |
|
xQ x | |
|
|
|
|
xP x . |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x P x Q x |
|
|
x P x Q x 1; |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x P x Q x |
|
x P(x) Q x 0 ; |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
xP x |
xQ x , |
|
xQ x | |
|
|
|
xP x . |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
x P x |
Q x |
|
x P x |
|
|
Q x 1; |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
x P x Q x |
|
|
x P(x) Q x 0; |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
x P x |
Q x , |
|
xQ x | |
|
|
|
|
xP x . |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
x P x Q x |
|
x P x Q x 1; |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
x P x Q x |
|
x Q x |
P(x) 0 ; |
|||||||||||||||||||||||||||||||
x P x Q x , |
xP x | |
|
|
|
x P x Q x . |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
x P x Q x |
x P x Q x 1; |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
x P x Q x |
|
|
|
|
|
|
x Q x |
|
|
|
|
|
P(x) 0 ; |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
xP x |
xQ x , |
|
xQ x | |
|
|
|
|
|
xP x . |
|||||||||||||||||||||||||
65
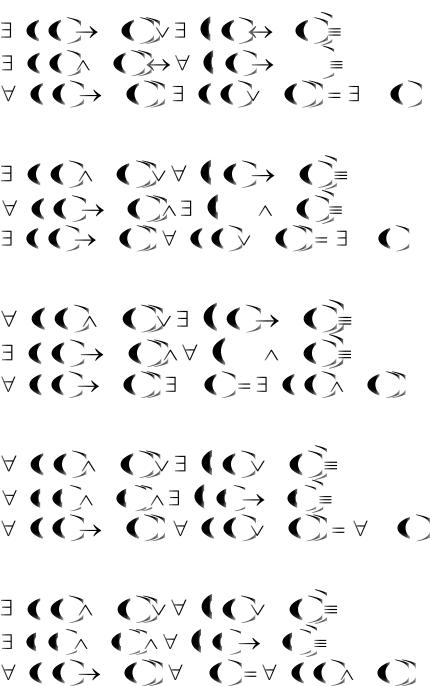
Вариант 21. а)
б) в)
Вариант 22. а)
б) в)
Вариант 23.
а)
б) в)
Вариант 24. а)
б) в)
|
|
|
|
|
|
x P x Q x |
x P x |
Q x 1; |
|||
|
|
|
|
|
|
x P x Q x |
x Q x |
|
P(x) 0 ; |
||
x P x Q x , |
x P x Q x | xQ x . |
||||
|
|
|
|
|
x P x Q x |
x Q x P x 1; |
|||
|
|
|
|
|
x P x Q x |
x P(x) Q x 0 ; |
|||
x P x Q x , |
x P x Q x | xQ x . |
|||
|
|
|
|
|
x P x Q x |
x Q x |
|
P x 1; |
|
|
|
|
|
|
x P x Q x |
x P(x) Q x 0 ; |
|||
x P x Q x , |
xP x | |
x P x Q x . |
||
|
|
|
|
|
|
x P x Q x |
x P x Q x 1; |
||||
|
|
|
|
||
x P x Q x |
x Q x P x 0 ; |
||||
x P x Q x , |
x P x Q x | xQ x . |
||||
Вариант 25. а)
б) в)
|
|
|
|
|
|
|
|
x P x Q x |
x P x Q x 1; |
||||||
|
|
|
|
|
|||
x P x Q x |
x Q x |
|
P x 0 ; |
||||
x P x Q x , |
xP x | |
|
|
x P x Q x . |
|||
66
Лабораторная работа 8
ЛОГИЧЕСКИЕ ИСЧИСЛЕНИЯ. АКСИОМАТИЧЕСАЯ ТЕОРИЯ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ
Цель работы
Доказать выводимость формул в исчислении высказываний из данных гипотез. Доказать теоремы исчисления высказываний.
Краткая теория
Логическая система исчисления высказываний – это аксиоматическое представление алгебры высказываний. Аксиоматическое построение теории предполагает вывод рассматриваемых в теории формул из конечного числа аксиом при помощи правил вывода. В качестве аксиом выбираются тождественно истинные формулы алгебры высказываний. Аксиоматический подход даѐт возможность построения логической системы без учѐта содержательной интерпретации рассматриваемых
формул. |
|
|
|
|
|
|
|
Понятие формулы определяется следующим образом: |
|||||
1) |
каждая пропозициональная переменная является формулой; |
|||||
|
|
|
|
|
|
|
2) |
если F, F |
и F |
– формулы, то F , ( F |
F ) – также являются |
||
|
1 |
2 |
1 |
2 |
||
формулами;
3)других формул нет.
Вкачестве аксиом выбираются следующие формулы:
A1. |
F (G |
F) ; |
||||||
A2. |
(F (G F)) ((F G) (F H)) ; |
|||||||
|
|
|
|
|
|
|
||
A3. |
(G F ) |
((G F ) G)) , |
||||||
где F, G, H – произвольные формулы.
Основным правилом вывода (ПВ) является правило заключения: из формулы F и формулы F G следует формула G.
Выводом формулы F из множества формул Г называется конечная
последовательность формул B1, B2, … , Bs = F, каждая из которых является либо аксиомой, либо формулой из множества Г, либо получена, из предыдущих формул этой последовательности, по правилу вывода. Элементы множества Г, при этом, называются гипотезами или посылками вывода, а формула F – выводимой из множества формул Г.
Обозначение выводимости: Г |= F.
Формула F называется доказуемой, если существует конечная последовательность формул B1, B2, … , Bs, где Bs = F, каждая из которых является либо аксиомой, либо формулой, полученной из предшествующих
67

формул этой последовательности, при помощи правила вывода. Формула F
в этом случае называется теоремой, а последовательность Bi – доказательством теоремы F. Обозначения для теорем: |= F.
Вывод формул и доказательство многих теорем значительно упрощается в результате применения основных теорем исчисления высказываний. Такими теоремами являются следующие теоремы.
Теорема 1. (О дедукции). Если из гипотез F1, F2, … , Fn выводится
формула G, то из гипотез F1, F2, …, Fn-1 выводима формула Fn G, то есть
F1, F2, … , Fn |= G => F1, F2, … , Fn-1 |= Fn G.
Теорема 2. Для любых формул F и G следующие формулы являются теоремами исчисления высказываний:
а) F F ; б) F F ; в) (F G) (G F ) .
Формулы а) и б) из теоремы 2 называются законами двойного отрицания, а формула в) – законом контрапозиции.
Порядок выполнения работы
1.Доказать выводимость следующих формул из данных гипотез.
2.Доказать, что следующие формулы являются теоремами исчисления высказываний.
3.Доказать следующие теоремы исчисления высказываний.
Образец выполнения заданий
При помощи теоремы дедукции а) доказать выводимость следующих формул из данных гипотез; б) при помощи законов двойного отрицания и теоремы дедукции доказать, что следующие формулы являются теоремами исчисления высказываний; в) при помощи закона контрапозиции и теоремы дедукции доказать следующие теоремы:
а) a (b c), a b | a c ; |
|
|||||||
|
|
|
|
|
|
|
|
|
б) | (b a) |
(b a ) ; |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
в) | (a b) |
((c |
b ) (a |
c)). |
|||||
Решение. а) Сначала к данным гипотезам a |
(b c) и a b |
|||||||
добавим новую гипотезу а и получим вывод формулы c. То есть построим последовательность формул, которая будет выводом формулы c:
68

1. a |
(b c) – гипотеза; |
|
2. a |
b – гипотеза; |
|
3. a |
– новая гипотеза; |
|
4. b |
c – получена из (3) и (1) по ПВ; |
|
5. b |
– получена из (3) и (2) по ПВ; |
|
6. c |
– получена из (5) |
и (4) по ПВ. |
Таким образом, построили вывод формулы c из данных гипотез и новой гипотезы а, то есть, доказали следующую выводимость формулы с:
a (b c) , a b , a |= c.
После этого, применяя теорему о дедукции, получим искомую выводимость
a (b c) , a b |= a c .
Вывод формулы c можно также изобразить в виде дерева вывода:
|
|
a, a b a,a (b c) |
|
|
||
|
|
|
|
|
|
|
|
|
b |
|
b c |
|
. |
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
б) Сначала докажем, что |
из гипотез (b a) и b выводима |
|||||
формула a :
1.b a – гипотеза;
2.b – гипотеза;
3.a – получена из (2) и (1) по ПВ;
4.a a – теорема (закон двойного отрицания);
5.a – получена из (3) и (4) по ПВ.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Таким образом, получили вывод формулы |
a , то есть |
доказали |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выводимость b |
|
a , b |= |
a . |
|
|
|
|
|
|
|
|
|
|
|
||||
Применяя дважды теорему о дедукции, получим сначала |
||||||||||||||||||
выводимость |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
b |
a |= b |
a , затем искомую выводимость | |
(b |
a) (b |
|
a ) . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
| (a |
b) |
((c b ) |
|
(a |
c)) . |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
||||||||||||||
в) Построим сначала вывод формулы c из гипотез a |
b , c |
b , a : |
||||||||||||||||
1.a b– гипотеза;
2.c b – гипотеза;
3.a – гипотеза;
69

4.a a – теорема (закон двойного отрицания);
5.a – из (3) и (4) по правилу вывода;
|
|
|
|
|
|
|
|
|
|
|
6. (c |
b ) |
(b |
|
|
|
|
) –закон контрапозиции; |
|||
c |
||||||||||
7.b c – из (2) и (6) по правилу вывода;
8.b – из (5) и (1) по правилу вывода;
9.b b – теорема (закон двойного отрицания);
10.b – из (8) и (9) по правилу вывода;
11.c – из (10) и (7) по правилу вывода;
12.c c – теорема (закон двойного отрицания);
13.c – из (11) и (12) по правилу вывода.
Таким образом, получили вывод формулы с, то есть, доказали выводимость
a b, c b , a |= c.
Применяя последовательно теорему о дедукции, получим:
a b , c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
b |= |
a |
|
|
c ; |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
a b |= ( |
|
|
|
|
b ) |
|
(a |
|
|
|
c) ; |
|
|||||||||
c |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|= (a b) (( |
|
|
|
|
|
b ) |
|
|
|
|
|
(a |
c)) . |
|
|||||||
c |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Следовательно, формула (a b) |
|
|
|
|
(( |
|
|
|
|
b ) |
(a |
c)) является |
|||||||||
|
|
|
|
c |
|
|
|||||||||||||||
теоремой исчисления высказываний.
Вопросы для самопроверки
1.Определите понятие аксиоматической системы исчисления высказываний.
2.Напишите аксиомы исчисления высказываний.
3.Каким образом можно из трех аксиом получить бесчисленное множество аксиом?
4.Какая формула называется выводимой в исчислении высказываний?
5.Какая формула называется доказуемой в исчислении высказываний?
6.Что называется доказательством?
7.Что называется теоремой в исчислении высказываний?
8.Как связаны теоремы исчисления высказываний и тавтологии алгебры высказываний?
Литература: [2], часть 4, с. 76–77; [7], гл. 6, стр. 217–246. [12], § 6, стр.
85–94.
70
