Лабораторный Практикум по Дискрмат2

Вариант 14.

1) А B =( A B ) А; 2) B \ A =(А B ) A ; 3) (А\В)\С=(А\В) (А\С).

Вариант 15.

1) А В=А\( B \ A ); 2) B \ A =( A B ) А; 3) (А\В)\С=А\(В С).

Вариант 23.

1) А\В=(А\В) А; 2) А В=(А\ B )\ A ; 3) (А\В) С=(С\В) А.

Вариант 24.

1) А\В=( A B ) А; 2) А B =А ( B \ A ); 3) (А\С)\В=А\(В С).

Вариант 25.

1) A \ B = (А В) А; 2) А В=(А\ B ) В; 3) А\(В\С)=(А\В) (С\ A ).

в) Докажите равенство декартовых произведений множеств. Вариант 1.

А (В С)=(А В) (А С).

Вариант 2.

А (В С)=(А В) (А С).

Вариант 3.

А (В\С)=(А В)\(А С).

Вариант 4.

11

(А\В) С=(А С)\(В С).

Вариант 5.

(А В) С=(А С) (В С).

Вариант 6.

(А В) С=(А С) (В С).

Вариант 7.

(А B ) С=(А С)\(В С).

Вариант 8.

А (В C )=(А В)\(А С).

Вариант 9.

(А\В) С=(А С) ( B C ).

Вариант 10.

А (В\С)=(А В) ( A C ).

Вариант 11.

(А В) С=(А С)\( B C ).

Вариант 12.

А (В С)=(А В)\( A C ).

Вариант 13.

(А B ) С=(А С) ( B C ).

Вариант 14.

А (В C )=(А В) ( A C ).

Вариант 15.

(А В) С=(В С)\( A C ).

Вариант 16.

А (В С)=(А С)\( A B ).

Вариант 17.

( A B ) С=( A С) ( B C ).

Вариант 18.

(А В) (С D)=(A C) (B D).

Вариант 19.

A (B\C)=(A B) (A C ).

Вариант 20.

(A\B) C=(А С) ( B С).

12

Вариант 21.

(А В) (А С)=(А А) (В С).

Вариант 22.

А ( B C )=(А C ) ( A B ).

Вариант 23.

( A B ) С=( B С) ( A C ).

Вариант 24.

(А С) (В С)=(А В) (С С).

Вариант 25.

А ( B C )=(А B ) ( A C ).

Лабораторная работа № 2

ОТНОШЕНИЯ И ИХ СВОЙСТВА. ФУНКЦИОНАЛЬНОСТЬ ОТНОШЕНИЙ. КОМПОЗИЦИЯ ОТНОШЕНИЙ И ФУНКЦИЙ

Цель работы

Построить граф данного бинарного отношения и выяснить, какими свойствами оно обладает. Проверить функциональность отношения. Построить композицию отношений. Проверить обратимость отношения и найти обратное отношение для данного отношения.

Краткая теория

Отношением, заданным на множествах A1, A2,…, An, называется

любое подмножество R декартова произведения A1 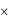A2 … An этих множеств. Число множеств, участвующих в декартовом произведении, называется местностью отношения. Двухместное отношение f, заданное на множествах A и B называется соответствием или отображением,

заданным на этих множествах. Отображение f называется отображением множества A в множество B, если для каждого элемента a A существует элемент b B такой, что элементы a и b находятся в отношении f, иначе, (a,b) f. Элемент b при этом называется образом элемента a при отображении f. Обозначение: f(a)=b. Элемент a при этом называется прообразом элемента b. Отображение f называется отображением множества A на множество B, если для каждого элемента b B существует хотя бы один прообраз, то есть такой элемент a A, что элементы a и b находятся в отношении f.

Пусть отношение f задано на множествах A и B, то есть

13

Отображение f множества A на множество B называется взаимно однозначным, если для каждого образа при отображении f существует единственный прообраз и для каждого прообраза существует единственный образ. Бинарное отношение f, заданное на множествах A и B, называется функциональным или функцией, если для любого элемента a A и любых элементов b B, c B из того, что (a,b) f и (a,c) f следует, что a=c.

Областью определения двухместного отношения, заданного на множествах A и B, называется множество

Dom(f)={a| a A, 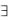b B, (a,b) f }.

Областью значений функции f называется множество

Im(f)={b| b B, 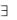a A, (a,b) f }.

Бинарное отношение f называется отношением, заданным на множестве A, если f является подмножеством, декартова произведения A A. Бинарное отношение f, заданное на множестве A, называется рефлексивным отношением, если для всех элементов a A, элемент (a, a) будет принадлежать множеству f. Отношение f называется антирефлексивным отношением, если для всех a A элемент (a, a) не будет принадлежать множеству f. Отношение f называется симметричным, если для всех элементов a A, b A при выполнении условия (a, b) f, будет выполнено также условие (b, a) f. Если a и b числа, то точки (a, b) и (b, a), будут располагаться в декартовой плоскости симметрично относительно биссектрисы y=x. Отношение f называется антисимметричным отношением, если для всех элементов a A, b A при выполнении условий (a, b) f и a b будет выполнено условие (b, a) f. Отношение f называется

транзитивным, если для всех элементов a A, b A c A, при одновременном выполнении двух условий (a, b) f и (b, c) f элемент (a, c) также будет принадлежать отношению f.

Бинарное отношение f, заданное на множестве A, называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно. Если на множестве A задано отношение эквивалентности, то это множество разбивается на непересекающиеся подмножества, классы эквивалентности. Отношение эквивалентности является основным понятием классификации математических объектов.

Пример. Отношение делимости, заданное на множестве целых чисел, является отношением эквивалентности.

Композицией двух функциональных отношений f и g, заданных соответственно на парах множеств A, B и B, C, называется новое

14

2.Проверить функциональность отношений f, g, h.

3.Построить композицию отношений f и g.

4.Проверить обратимость отношения f и найти обратное отношение для данного отношения.

Образец выполнения заданий

а) Построить граф бинарного отношения R:

R = {(1, 3), (2, 1), (3, 4), (4, 1), (4, 2)},

заданного на множестве А = {1, 2, 3, 4} и выяснить, какими свойствами оно обладает. Найти область определения и область значений отношения R.

б). Проверить функциональность отношений f, g, h:

на множестве А. Если отношения являются функциями - необходимо найти их область определения и область значений. R – множество действительных чисел.

и на каком множестве? Найти обратную функцию для функции f в области существования ее обратной.

Решение. а) Рассмотрим бинарное отношение

R = {(1, 3), (2, 1), (3, 4), (4, 1), (4, 2)},

заданное на множестве A={1, 2, 3, 4}. Построим граф отношения R. Для этого элементы множества A изобразим в виде точек на плоскости (вершины графа). Элементы отношения R изобразим в виде векторов (ребра графа), исходящих из той вершины, которая соответствует левой координате пары и входящей в вершину, соответствующую правой координате пары. В результате получим граф, изображенный на рисунке 5.

15

Выясним свойства, которыми обладает данное отношение. Отношение R не является рефлексивным, так как граф этого отношения не имеет векторы, исходящие и входящие в одни и те же вершины. В этом случае отношение будет антирефлексивным.

Отношение R не будет также симметричным, так как для симметричности отношения необходимо, чтобы все ребра графа были двояко направленными. Однако таких элементов граф не имеет. В этом случае граф будет антисимметричным.

Отношение R не будет транзитивным, так как, например, есть пара (1, 3) и пара (3, 4). Но не имеет отношение R пары (1, 4).

Отношение R не будет отношением эквивалентности, так как для этого необходимо, чтобы отношение R было рефлексивным, симметричным и транзитивным.

Областью определения отношения R является множество всех первых координат элементов этого отношения, то есть Dom(R)={1, 2, 3, 4}. Областью значений отношения R является множество всех вторых координат элементов этого отношения, то есть Im(R)={1, 2, 3, 4}.

б) Проверим функциональность отношения f={(1, 1), (1, 2), (2, 3), (3, 2)}. Согласно определению функциональности отношения каждый прообраз не может иметь более одного образа. Однако в двух элементах (1, 1) и (1, 2) отношения f прообраз 1 имеет два образа: 1 и 2. Следовательно, отношение f не является функциональным.

Проверим функциональность отношения g ={(1, 1), (2, 1), (3, 3), (4, 3)}. Каждый прообраз отношения g в данном случае имеет только один образ. Следовательно, отношение g является функциональным.

Проверим функциональность отношения h={(х, у) х2 + у2=х}, А=R. Функциональное отношение h задано неявно. Поэтому, сначала найдем

явное выражение для данного отношения: y= (x-x2)1/2. Это выражение показывает, что для каждого значения аргумента х, области определения, возможны два значения у. Следовательно, данное отношение не является функциональным на множестве всех действительных чисел. Однако отношение будет функциональным в ограниченной области определения.

16

Например, если множество А = R+, то есть, множеству всех неотрицательных действительных чисел, то отношение h будет функциональным в области своего определения. Область определения

отношения h: Dom(h)={х| x – x2 0} = [0, 1]. Область значений отношения h в этом случае будет Im(h)= [0, 1].

в) Найдем композиции функциональных отношений f и g:

f={(1, 2), (2, 3), (3, 4), (4, 1)}, g={( 1, 2), ( 2, 3), ( 3, 4), ( 4, 1)}.

Рассмотрим все элементы из области определения отношения f , Dom(f ) =

3. Рассматривая, таким образом, каждый элемент из области определения f, получим

Затем, заменяя аргумент функции φ на функцию ψ, получим композицию:

φ ψ = φ (ψ( х)) = (1 (2ctg x)2)1/2. Аналогично получим: ψ φ = ψ ((φ(х)) = =2ctg((1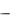x2)1/2).

г) Выясним, имеет ли функция f={(х, у) х5у=1} обратную функцию.

Для этого, выразим в явном виде данное отношение y=1/x5 и выясним его функциональность. Для каждого аргумента, из области определения, существует единственное значение y. Следовательно, данное отношение функциональное. Построим обратное отношение и проверим его функциональность. Для этого, согласно определению, в явном выражении

отношения сделаем замену х на y и наоборот: х =1/ y 5. После этого

найдем явное выражение y(х) =(1/x)1/5. Обратное отношение также функциональное. Таким образом, обратная функция для f существует на множестве всех действительных чисел. Область определения обратной функции – это множество R\{0}, область значений - также множество

R\{0}.

Вопросы для самопроверки

1.Что называется отношением?

2.Как связаны отношения и декартово произведение множеств?

3.Перечислите основные свойства отношений.

4.Какое отношение называется отношением эквивалентности?

17

5.Какое отношение называется функциональным?

6.Что называется обратным отношением?

7.В чем отличие отношений и функций?

Литература: [3], гл.1, с. 9–12; [2], Часть 2, с. 5–59; [7], гл. 1, стр. 9–16.

Задания для самостоятельной работы

а) Построить граф бинарного отношения R, заданного на множестве А={1, 2, 3, 4} и выяснить, какими свойствами оно обладает. Найти область определения и область значений R.

Вариант 1. R = {(1, 1), (1, 3), (2, 2), (2, 4), (3, 1), (3, 3), (4, 2), (4, 4)}. Вариант 2. R = {(1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2), (3, 3), (4, 4)}. Вариант 3. R = {(1, 1), (1, 4), (2, 2), (3, 2), (3, 3), (4, 1), (4, 4)}.

Вариант 4. R = {(1, 2), (1, 3), (2, 1), (2, 4), (3, 1), (3, 4), (4, 2), (4, 3)}. Вариант 5. R = {(1, 1), (1, 3), (2, 2), (3, 1), (3, 3), (3, 4), (4, 3), (4, 4)}. Вариант 6. R = {(1, 2), (1, 3), (2, 2), (2, 3), (3, 2), (3, 3), (4, 2), (4, 3)}. Вариант 7. R = {(1, 1), (1, 2), (2, 1), (2, 2), (3, 3), (3, 4), (4, 3), (4, 4)}. Вариант 8. R = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 4)}. Вариант 9. R = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2), (4, 4)}.

Вариант 10. R = {(1, 1), (1, 2), (2, 1), (2, 2), (2, 3), (3, 2), (3, 3), (4, 4)}. Вариант 11. R = {(1, 1), (1, 2), (2, 1), (2, 2), (3, 3), (3, 4), (4, 4)}. Вариант 12. R = {(1, 1), (1, 3), (2, 1), (2, 3), (3, 1), (3, 3), (4, 1), (4, 3)}. Вариант 13. R = {(1, 1), (1, 4), (2, 2), (2, 3), (3, 2), (3, 3), (4, 1), (4, 4)}. Вариант 14. R = {(1, 2), (1, 3), (1, 4), (2, 2), (3, 2), (3, 3), (3, 4), (4, 2)}. Вариант 15. R = {(1, 1), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (4, 4)}. Вариант 16. R = {(1, 1), (1, 3), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3), (4, 4)}. Вариант 17. R = {(1, 1), (1, 3), (2, 2), (2, 4), (3, 1), (3, 3), (4, 4)}. Вариант 18. R = {(1, 1), (1, 4), (2, 1), (2, 4), (3, 1), (3, 4), (4, 1), (4, 4)}. Вариант 19. R = {(1, 2), (1, 4), (2, 1), (2, 3), (3, 2), (3, 4), (4, 1), (4, 3)}. Вариант 20. R = {(1, 1), (1, 2), (1, 3), (2, 2), (3, 2), (4, 1), (4, 2), (4, 3)}. Вариант 21. R = {(1, 2), (1, 4), (2, 1), (2, 2), (2, 4), (3, 3), (4, 1), (4, 2)}. Вариант 22. R = {(1, 1), (1, 4), (2, 2), (3, 3), (3, 4), (4, 1), (4, 3), (4, 4)}. Вариант 23. R = {(1, 1), (1, 4), (2, 2), (2, 3), (3, 2), (3, 3), (4, 4)}. Вариант 24. R = {(1, 1), (1, 2), (2, 1), (2, 2), (3, 1), (3, 2), (4, 1), (4, 2)}. Вариант 25. R = {(1, 3), (1, 4), (2, 3), (2, 4), (3, 1), (3, 2), (4, 1), (4, 2)}.

б) Проверить функциональность отношений f , g, h на множестве А. Если отношения функциональны, то найти их область определения и область значений. (В примерах 1, 2 множество А = {1, 2, 3, 4}.)

Вариант 1. f={(1, 1), (1, 2), (2, 1), (3, 1)}; g ={(1, 1), (2, 1), (3, 2), (4, 2)};

18

h = {(х, у) х2+у2= – х}, А=R.

h = {(х, у) х2+1= ху}, А= R.

Вариант 10. f={(1, 3), (2, 3), (3, 1), (3, 2)}; g ={(1, 3), (2, 4), (3, 1), (4, 2)}; h = {(х, у) х2 1= ху}, А= R.

Вариант 11. f={(1, 2), (2, 3), (3, 4), (2, 1)}; g ={(1, 1), (2, 1), (3, 1), (4, 3)}; h = {(х, у) х2+у2=1}, А= R +.

Вариант 12. f={(1, 2), (2, 3), (2, 4), (4, 2)}; g ={(1, 1), (2, 1), (3, 3), (4, 3)}; h = {(х, у) у =1+ ух2}, А= R.

Вариант 13. f={(1, 4), (2, 3), (4, 1), (4, 3)}; g ={(1, 4), (2, 3), (3, 3), (4, 1)}; h = {(х, у) 2х ху = 2у 1}, А= R.

Вариант 14. f={(1, 2), (2, 1), (2, 3), (3, 2)}; g ={(1, 2), (2, 1), (3, 2), (4, 3)}; h = {(х, у) ln(х2) = ln (у)}, А= R.

Вариант 15. f={(1, 2), (2, 3), (3, 2), (3, 1)}: g ={(1, 1), (2, 1), (3, 3), (4, 4)};

19

h = {(х, у) х2+у2= 4х}, А= R +.

Вариант 16. f={(1, 3), (2, 3), (3, 3), (1, 4)}; g ={(1, 3), (2, 1), (3, 4), (4, 1)}; h = {(х, у) ln(х) = ln(у)}, А= R.

Вариант 17. f={(1, 3), (3, 2), (2, 3), (3, 1)}; g ={(1, 1), (2, 2), (3, 2), (4, 1)}; h = {(х, у) х + у = ху}, А= R.

Вариант 18. f={(1, 1), (1, 3), (2, 2), (2, 4)}; g ={(1, 1), (2, 3), (3, 3), (4, 3)}; h = {(х, у) х2у2+ 4 = 4ху}, А= R.

Вариант 19. f={(1, 2), (2, 3), (1, 4), (2, 4)}; g ={(1, 3), (2, 3), (3, 4), (4, 4)}; h = (х, у) х2 у2=4}, А= R +.

Вариант 20. f={(1, 1), (1, 3), (1, 4), (4, 2)}; g ={(1, 1), (2, 1), (3, 1), (4, 1)}; h = {(х, у) х у = ху}, А= R.

Вариант 21. f={(1, 2), (2, 2), (3, 2), (1, 4)}. g ={(1, 2), (2, 2), (3, 3), (4, 3)}; h = {(х, у) х2+ у2=2х}, А= R +.

Вариант 22. f={(1, 1), (1, 2), (2, 3), (2, 4)}; g ={(1, 1), (2, 1), (3, 2), (4, 4)}; h = {(х, у) ln(х) ln(у)=1}, А= R.

Вариант 23. f={(1, 2), (2, 2), (1, 4), (2, 4)}; g ={(1, 4), (2, 4), (3, 2), (4, 2)}; h = {(х, у) х2у2+1= 2ху}, А= R.

Вариант 24. f={(3, 1), (4, 1), (3, 2), (4, 2)}; g ={(1, 2), (2, 3), (3, 3), (4, 3)}; h = {(х, у) ln(х) + ln(у)=1}, А= R.

Вариант 25. f={(1, 4), (2, 4), (3, 4), (1, 2)}; g ={( 1, 3), ( 2, 4), ( 3, 2),

( 4, 1)};

h = {(х, у) x1/2 – y1/2=1}, А= R.

в) Для функциональных отношений f , g, φ и ψ найдите композиции g f , f g, ψ φ, φ ψ.

20