Лабораторный Практикум по Дискрмат2

Таблица 13.

Машина Тьюринга с алфавитом внутренних состояний {q0, q1, q2, q3, q4, q5, q6, q7}.

Выяснить применимость машины к слову A. В случае применимости преобразовать слово A при помощи данной машины. В начальном состоянии машина читает правую крайнюю единицу данного слова.

б) Машина Тьюринга с внешним алфавитом {0, 1, *} и алфавитом внутренних состояний {q0, q1, q2, q3} задана в виде следующей программы:

Таблица 14.

Машина Тьюринга с алфавитом внутренних состояний {q0, q1, q2, q3}.

Преобразовать слово B при помощи данной машины при условии, что в начальном состоянии машина читает правую крайнюю единицу данного

141

Практическое занятие № 8

КОНСТРУИРОВАНИЕ МАШИН ТЬЮРИНГА. АЛГОРИТМИЧЕСКИ РАЗРЕШИМЫЕ И НЕРАЗРЕШИМЫЕ

ЗАДАЧИ

Цель работы

Построить машину Тьюринга, которая вычисляет значения данной арифметической функции. При помощи операции подключения машин Тьюринга построить новую машину Тьюринга, вычисляющую значения данной арифметической функции.

Краткая теория

Основной задачей теории алгоритмов является уточнение интуитивного понятия алгоритма путем конструирования машин Тьюринга. Алгоритмическая разрешимость какой-либо задачи при этом становится равносильным существованию машины Тьюринга, реализующей решение этой задачи. То есть, если будет доказано, что для некоторой конкретной задачи невозможно построить машину Тьюринга, решающую эту задачу, то такая задача будет алгоритмически

142

неразрешимой. Если же можно построить машину Тьюринга, то разрешимой задачей. При этом, задачи могут быть не только математические и не только теоретические. Задачи могут быть любые. Но применяется теория алгоритмов для решения наиболее трудных задач, алгоритмическая разрешимость которых подвергается сомнению. Реализуя решение некоторой задачи на любом алгоритмическом языке, по сути, доказывается алгоритмическая разрешимость задачи. В этом отношении язык команд машины Тьюринга является одним из алгоритмических языков.

Язык команд машины Тьюринга применяется только в особых случаях и по той причине, что составить программу при помощи этих команд сложнее, чем при помощи команд большинства алгоритмических языков. Для того, чтобы убедиться в этом, достаточно сформулировать любую достаточно сложную задачу и попытаться построить машину Тьюринга, решающую эту задачу. Вместе с тем, известны определенные правила и рекомендации, которые позволяют процесс программирования сделать более простым. Поэтому, прежде всего, рассмотрим на конкретных примерах эти правила и рекомендации.

Основное правило является общим для составления любой программы на любом алгоритмическом языке и состоит в максимально возможной мысленной детализации решаемой задачи:

а) изобразить преобразуемое слово на ленте; б) разработать конкретные шаги действий, которые привели бы к

необходимому преобразованию; в) записать эти действия в виде команд машины Тьюринга.

Задача 1. В ячейках ленты записано слово из n единиц. Необходимо построить машину Тьюринга, которая находит крайнюю левую единицу этого слова и завершает свою работу. В начальном состоянии q1 машина читает одну из единиц данного слова.

Решение. Прежде всего, выберем внешний алфавит. Так как данное слово состоит из единиц, то достаточно включить во внешний алфавит символ 1 и любой символ для обозначения пустой ячейки, например, 0. В результате, получим внешний алфавит машины {0, 1}. Алфавит внутренних состояний при конструировании машин заранее не выбирается. Символы алфавита присоединяются к алфавиту по мере их необходимости. Запишем на ленте n единиц. Конкретные шаги в данном случае будут состоять в следующем: согласно условию задачи необходимо выполнить перемещение читающего устройства влево. Так как в условиях задачи не указана конкретная единица слова, то сдвиг влево лучше выполнить многократный, циклический. Циклический сдвиг получится в том случае, если выполняя команду не изменять внутреннее состояние машины. Таким образом, первым элементом программы будет следующая команда q11 q11L. Действие этой команды будет продолжаться до тех

143

пор, пока в состоянии q1 машина не будет читать символ пустой ячейки, то есть 0. Следовательно, следующая команда машины должна остановить движение читающего устройства влево, не изменяя содержания ячейки. Это можно сделать путем изменения внутреннего состояния машины. В результате получим следующую команду q10 q20R. Это действие программы не только останавливает смещение влево, но и выполняет сдвиг вправо на одну позицию. При этом заранее можно сказать, что после такого сдвига машина в состоянии q2 будет читать левый крайний символ 1 данного слова. То есть, найдена левая крайняя единица данного слова. Поэтому, достаточно завершить работу машины. Завершает работу машины команда q21 q01S. В результате, получим следующую программу, решающую сформулированную задачу:

q11 q11L q10 q20R q21 q01S.

Задача 2. В ячейках ленты записано слово из n единиц. Необходимо построить машину Тьюринга, которая преобразует это слово в пустое слово и завершает свою работу. В начальном состоянии q1 машина читает одну из единиц данного слова.

Решение. Выберем в качестве внешнего алфавита множество символов {0, 1}. Начальное положение читающего устройства, согласно условию задачи, не вполне определено. Поэтому организуем циклический сдвиг читающего устройства вправо или влево для того, чтобы читающее устройство занимало одно из крайних позиций по отношению к слову, записанному на ленте. Например, при помощи команды q11 q11R выполним циклический сдвиг вправо. После того, как машина прочитает первый символ пустой ячейки, необходимо сменить внутреннее состояние машины и выполнить сдвиг влево. Выполним эти действия командой q10 q20L. После сдвига влево машина прочитает правый крайний символ 1 данного слова. Начиная с этого символа можно при помощи одной команды заменить все символы 1 слова на символ пустой ячейки 0. Такой командой будет q21 q20L. Появление первого символа пустой ячейки будет означать, что все символы 1 заменены на символы 0 и задача решена. Поэтому можно применить команду, останавливающую работу машины: q20 q00S. В результате, получим следующую программу:

q11 q11R q10 q20L q21 q20L q20 q00S.

144

Последовательное подключение машин. Конструирование машин становится более эффективным, если удается использовать уже построенные программы, последовательно подключая их в композицию машин. Рассмотрим способ построения композиции двух машин. Пусть машина Тьюринга T1 имеет внешний алфавит {a0, a1, … , an} и алфавит внутренних состояний {q0, q1, … , qm}, а машина T2 имеет тот же внешний алфавит и алфавит внутренних состояний {q0, q1, … , qs}. Обозначим через T2 T1 новую машину, которая работает сначала по программе машины T1, затем по программе машины T2. Программа машины T2 T1 получается из программ машин T1 и T2 следующим образом. Программа машины T1 переносится в новую машину почти без изменений за исключением символа окончания работы машины q0. Этот символ необходимо заменить символом внутреннего состояния qm+1. Символы внутренних состояний машины T2 необходимо перенумеровать следующим образом: символ q1 необходимо заменить символом qm+1, символ q2 необходимо заменить на qm+2 и так далее, символ qs заменить на qm+s. Символ q0 окончания работы машины T2 остается без изменения в новой машине. В результате получим композицию T2 T1. Аналогично строится композиция T1 T2.

Вычисление значений функций. Последовательное подключение машин Тьюринга позволяет провести детализацию процесса вычисления значений функций. Сначала можно построить машины Тьюринга, выполняющие отдельные арифметические операции, затем, применить эти машины для вычисления значений функций.

Порядок выполнения работы

1.Построить машину Тьюринга, которая вычисляет значения данной арифметической функции.

2.При помощи операции подключения машин Тьюринга построить

а) На ленте записано слово из x и y единиц (x y), разделенное символом (*). Построить машину Тьюринга, которая преобразует данное слово, в слово, содержащее x - y единиц. В начальном состоянии машина читает правую крайнюю единицу данного слова.

б) На ленте записано слово из x единиц. Построить машину Тьюринга, которая преобразует данное слово, в слово, содержащее 2x единиц. В начальном состоянии машина читает 0 справа от правой крайней единицы данного слова.

Решение. а) Анализ работы машины Тьюринга, которая рассматривалась в качестве примера в практическом занятии 7 (образец,

145

задание б), показывает, что рассматриваемая там машина выполняет арифметическое действие - сложение. Аналогично этой машине строится следующая машина, которая выполняет вычитание:

Проверить работу этой машины предлагается в качестве самостоятельной работы.

б) Построим машину Тьюринга, которая удваивает число единиц на ленте. Для этого составим следующий алгоритм удвоения. В начальном положении машина читает символ 0, расположенный справа от крайней правой единицы данного слова.

1) Приписываем справа от символа 0 две единицы.

2) Образуем цикл, сдвигающий читающее устройство в левое крайнее положение.

3) Стираем крайнюю левую единицу.

4) Возвращаем читающее устройство в исходное положение.

Далее все действия повторяются до тех пор, пока в исходном слове не останется ни одной единицы. После чего машина завершает свою работу. Составим программу, реализующую эти действия, и запишем команды в табличной форме:

Проверим работу построенной машины. В начальный момент конфигурация слова на ленте имеет следующий вид: 11… 11q10. Применяя команды, записанные в таблице, получим последовательность слов:

146

данной пары в нумерации Кантора. Для данного номера пары в нумерации Кантора определить левую и правую координату пары.

Краткая теория

Теория рекурсивных функций является еще одним способом уточнения понятия алгоритма. Рассматривая примеры конструирования машин Тьюринга, выяснили, что любую машину Тьюринга можно представить или построить в виде композиции простых машин, выполняющих элементарные операции. Аналогичным образом строится теория рекурсивных функций. Сначала выбираются наиболее простые, базисные функции:

1)S(x) = x + 1 – функция следования;

2)O(x) = 0 – нуль – функция;

Затем, определяются операторы, при помощи которых получаются другие числовые функции. Определим эти операторы.

Оператор суперпозиции. Будем говорить, что функция (x1 , x2 ,..., xn ) получена из m – местной функции (x1 , x2 ,..., xm ) и n – местных функций f1,

f2, …, fm с помощью оператора суперпозиции, если для любых значений переменных x1, x2, …, xn выполняется равенство:

(x1 , x2 ,..., xn ) = ( f1 (x1 , x2 ,..., xn ), f2 (x1 , x2 ,..., xn ) , …, fm (x1 , x2 ,..., xn ) ).

Оператор примитивной рекурсии. Будем говорить, что (n + 1) –

местная функция 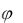получена из n – местной функции f и (n + 2) – местной функции g при помощи оператора примитивной рекурсии, если для любых значений переменных x1, x2, …, xn выполняются условия:

(x1 , x2 ,..., xn ,0) = f (x1 , x2 ,..., xn ),

(x1 , x2 ,..., xn , y 1) = g(x1 , x2 ,..., xn , y, (x1 , x2 ,..., xn , y) ).

Оператор минимизации. Будем говорить, что n – местная функция (x1 , x2 ,..., xn ) получена из (n + 1) – местных функций f1 и f2 при помощи

оператора минимизации, если для любых значений переменных x1, x2, …, xn , y равенство (x1 , x2 ,..., xn ) y выполняется тогда и только тогда,

выполняются следующие условия:

f1 (x1 , x2 ,..., xn ,0) 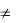f2 (x1 , x2 ,..., xn ,0) , f1 (x1 , x2 ,..., xn ,1) 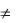f2 (x1 , x2 ,..., xn ,1) ,

149

наименьшему значению аргумента y, при котором выполняется равенство:

f1 (x1 , x2 ,..., xn , y)= f2 (x1 , x2 ,..., xn , y) .

Определение 1. Функция называется примитивно-рекурсивной, если ее можно получить из базисных функций при помощи конечного числа применений операторов суперпозиции, примитивной рекурсии.

Определение 2. Частично определенная функция называется рекурсивной, если ее можно получить из базисных функций при помощи конечного числа применений операторов суперпозиции, примитивной рекурсии и минимизации.

Если функция всюду определена и рекурсивна, то она называется

общерекурсивной.

Рассмотрим примеры примитивно-рекурсивных функций. Докажем, что операция сложения, вычитания и умножения являются примитивнорекурсивными функциями.

Пример 1. Рассмотрим операцию вычитания, определенную следующим образом:

x ÷ y = x y,при x y . 0, при x y

Сначала докажем, что функцию x ÷ 1 можно получить из базисных функций O(x), I12 (x, y) при помощи оператора примитивной рекурсии. В самом деле, по определению оператора примитивной рекурсии получим:

0 ÷ 1= 0 = O(x),

(x + 1) ÷ 1 = (x + 1) – 1 = x = I12 (x, y).

Докажем теперь, что функцию x ÷ y можно получить при помощи оператора примитивной рекурсии из функции I12 (x, y) и функции x ÷ 1. В самом деле, по определению оператора примитивной рекурсии получим:

150