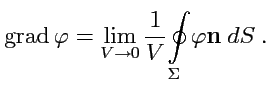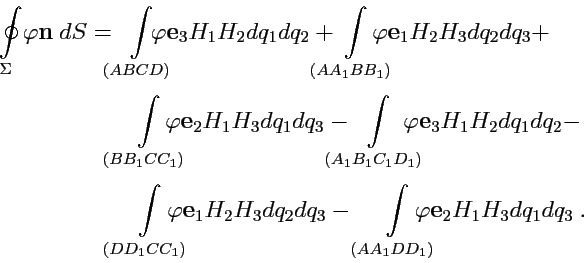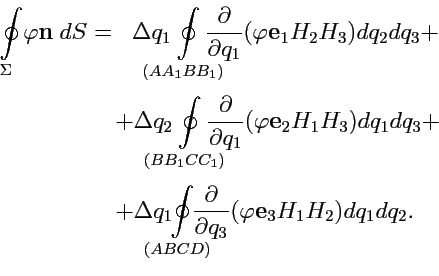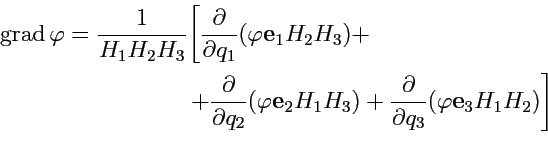FTF 2 semestr.MARTINOV / 19

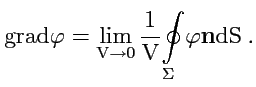
1. Градиент скалярного поля. Пусть дано скалярное поле . Согласно  определяется как предел:

(225)

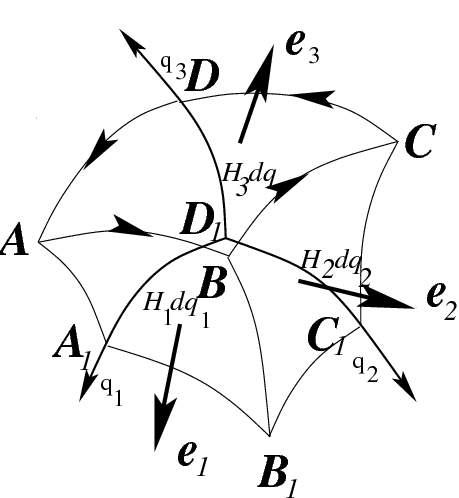
Рис.44 У вычислению интегралов вида (225)

Пусть также в области определения поля  задана криволинейная ортогональная система координат. Рассмотрим в качестве поверхности в (225) бесконечно малый параллелепипед объема  (рис. 44) (его гранями будут координатные поверхности). Тогда, в силу малости этого параллелепипеда, нормаль к каждой грани будет совпадать с соответствующим вектором репера:  и т. д. Учитывая, что, например, на грани   и аналогично на остальных, получим:

(226)

Знак "минус" в последних трех слагемых появляется так как нормаль должна быть направлена во внешнюю область замкнутой поверхности.

(227)

Применяя теорему о среднем к (227), переходим к пределу в (225):

	(228)
		(229)

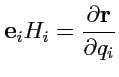Так как , ,  и , то второе слагаемое в (229) преобразуется к виду:

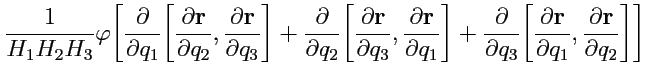
и обращается в ноль по свойству смешанных производных. Таким образом, формула для вычисления градиента скалярной функции в криволинейной ортогональной системе координат принимает вид:

(230)