FTF 2 semestr.MARTINOV / 1

Скалярное поле

Если каждой точке M некоторой области некоторого пространства (чаще всего подразумевается, что размерность этого пространства больше единицы) поставлено в соответствие некоторое (обычно — действительное) число u, то говорят, что в этой области задано скалярное поле. Другими словами, скалярное поле — это функция, отображающая Rⁿ в R (скалярная функция точки пространства). Точка пространства при этом на практике может быть указана или просто символически, или с помощью вектора (если пространство может быть представлено как векторное) или набором координат.

• Функция трёх переменных: 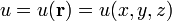 (скалярное поле на (в) трехмерном пространстве, называемое иногда^[1] пространственным полем).

• Функция двух переменных: 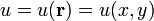 (скалярное поле на (в) двумерном пространстве, называемое иногда^[1] плоским полем).

• В физике и многих других приложениях поле, как правило, вообще говоря зависит также от времени^[2]:

,

Поверхность уровня

Скалярное поле можно представить графически с помощью поверхностей уровня (также называемой изоповерхностями).

Поверхностью уровня скалярного поля  называется множество точек пространства, в которых функция u принимает одно и то же значение c, то есть поверхность уровня определяется уравнением .

Для поля на двумерном пространстве аналогом поверхности уровня является линии уровня. Примеры: изобата, изотерма, горизонталь на географической карте и прочие изолинии.

Поверхностями уровня для скалярного поля на пространстве большей размерности являются гиперповерхности размерности на единицу меньшей, чем размерность пространства.

Для наглядного изображения скалярного поля используются поверхности уровня и линии уровня.        Поверхность уровня представляет собой множество всех точек пространства с одинаковыми значениями скалярного поля  . В любой точке поверхности уровня поле    принимает одно и то же значение  C  и, следовательно, уравнение поверхности уровня скалярного поля    имеет вид

      Например, поверхности уровня потенциала точечного зарада, расположенного в начале прямоугольной системы координат, описываются уравнением

x² + y² + z² = C

и, таким образом, представляют собой сферические поверхности.

  Рис. 1. Поверхность уровня потенциала точечного заряда. 

      Очевидно, что никакие две поверхности уровня    и    не могут иметь общих точек, если  . В противном случае это означало бы, что поле    одновременно принимает различные значения в одной и той же точке пространства.         Для некоторых поверхностей уровня используются специальные названия.

• Поверхности постоянной температуры называются изотермическими или изотермами.

• Поверхности постоянного давления называются изобарическими или изобарами.

• Поверхности постоянного потенциала называются эквипотенциальными.

• Поверхности постоянной энергии называются изоэнергетическими.

       Поле, величина функции которого зависит только от расстояния  r  до некоторого центра, называется центральным или сферическим.         Поверхности уровня центрального поля представляют собой концентрические сферы с центром в точке расположения источника поля. В сферической системе координат такие поверхности описываются уравнением  r = const.

  Рис. 2. Поверхности уровня центрального поля. 

       Поле    называется аксиально-симметричным, если функция    зависит только от расстояния  r  до некоторой оси.         Поверхностями уровня такого поля являются круговые цилиндры, оси которых совпадают с осью поля.

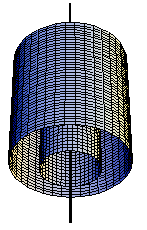  Рис. 3. Поверхности уровня аксиально-симметричного поля. 

       Аксиально-симметричное поле называют также цилиндрическим или осевым.         В цилиндрической системе координат поверхности уровня аксиально-симметричного поля описываются уравнением  r = const.