FTF 2 semestr.MAVRODI / 59

Признак Вейерштрасса равномерной сходимости функционального ряда.

Теорема. Если для функционального ряда (1) можно указать такой

сходящийся числовой ряд , что для всех nи для всех выполняется

условие 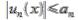(2), то ряд (1) сходящегося абсолютно и равномерно на множестве Е.

Д-во: По условию (2) для любого n, любого p и для каждого

Из (3) и (4) следует, что для ряда (1) выполняется. Условие Коши на множестве Е, в силу этого по критерию Коши — ряд сходящийся равномерно на множестве

Е. Абсолютная сходимость ряда для каждого следует из правой части (3).

Следствие: Если сходится ряд 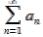, где =sup, , то ряд (2) сходится абсолютно и равномерно на множестве Е.