FTF 1 semestr.SHECOLDIN / 38

Вязкость жидкостей

Динамический коэффициент вязкости

Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Справедлив общий закон внутреннего трения — закон Ньютона:

Коэффициент вязкости  (динамическая вязкость) может быть получен на основе соображений о движениях молекул. Очевидно, что  будет тем меньше, чем меньше время t «оседлости» молекул. Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля-Андраде:

Иная формула, представляющая коэффициент вязкости, была предложена Бачинским. Как показано, коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества . Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение

где с и b — константы. Это эмпирическое соотношение называется формулой Бачинского.

Динамическая вязкость жидкостей уменьшается с увеличением температуры, и растёт с увеличением давления.

Ламина́рное тече́ние (лат. lāmina — «пластинка») — течение, при котором жидкость или газ перемещается слоями без перемешивания и пульсаций (то есть беспорядочных быстрых изменений скорости и давления).

Турбуле́нтность, устар. турбуле́нция (от лат. turbulentus — бурный, беспорядочный), турбуле́нтное тече́ние — явление, заключающееся в том, что при увеличении скорости течения жидкости или газа в среде самопроизвольно образуются многочисленные нелинейные фрактальные волны и обычные, линейные различных размеров, без наличия внешних, случайных, возмущающих среду сил и/или при их присутствии. Для расчёта подобных течений были созданы различные модели турбулентности. Волны появляются случайно. То есть их размер и амплитуда меняется хаотически в некотором интервале. Они возникают чаще всего либо на границе, у стенки, и/или при разрушении или опрокидывании волны. Они могут образоваться на струях. Экспериментально ее можно наблюдать на конце струи пара из электрочайника. Турбулентность экспериментально открыта английским инженером Рейнольдсом в 1883 году при изучении течения несжимаемой жидкости (воды) в трубах.

Число Рейно́льдса (), — безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье — Стокса^[1]. Число Рейнольдса также считается критерием подобия течения вязкой жидкости.

Число Рейнольдса определяется следующим соотношением:

где

•  — плотность среды, кг/м³;

•  — характерная скорость, м/с;

•  — характерный размер, м;

•  — динамическая вязкость среды, Н·с/м²;

•  — кинематическая вязкость среды, м²/с() ;

•  — объёмная скорость потока;

•  — площадь сечения трубы.

Тече́ние Пуазёйля — ламинарное течение жидкости через каналы в виде прямого кругового цилиндра или слоя между параллельными плоскостями. Течение Пуазёйля — одно из самых простых точных решений уравнений Навье — Стокса. Описывается законом Пуазёйля(Хагена — Пуазёйля).

Закон Пуазёйля (иногда закон Хагена — Пуазёйля) — это физический закон так называемого течения Пуазёйля, то есть установившегося течения вязкой несжимаемой жидкости в тонкой цилиндрической трубке. Закон установлен эмпирически в 1839 году Г. Хагеном, а в 1840—1841 годы — независимо Ж. Л. Пуазёйлем. Теоретически объяснён Дж. Г. Стоксом в 1845 году.

При установившемся ламинарном движении вязкой несжимаемой жидкости сквозь цилиндрическую трубу круглого сечения секундный объёмный расход прямо пропорционален перепаду давления на единицу длины трубы и четвертой степени радиуса и обратно пропорционален коэффициенту вязкости жидкости.

где

•  — перепад давления на концах капилляра, Па;

•  — секундный объёмный расход жидкости, м³/с;

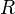•  — радиус капилляра, м;

•  — диаметр капилляра, м;

•  — коэффициент динамической вязкости, Па·с;

•  — длина трубы, м.

Формула используется для определения вязкости жидкостей. Другим способом определения вязкости жидкости является метод, использующий закон Стокса.