Закон Стокса

В 1851 Джордж Стокс получил выражение для силы трения (также называемой силой лобового сопротивления), действующей на сферические объекты с очень маленькими числами Рейнольдса (например, очень маленькие частицы) в непрерывной вязкой жидкости, решая уравнение Навье — Стокса:

где

•  — сила трения, так же называемая силой Стокса,

•  — радиус сферического объекта,

•  — динамическая вязкость жидкости,

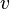•  — скорость частицы.

Если частицы падают в вязкой жидкости под действием собственного веса, то установившаяся скорость достигается, когда эта сила трения совместно с силой Архимеда точно уравновешиваются силой гравитации. Результирующая скорость равна

где

• V_s — установившаяся скорость частицы (м/с) (частица движется вниз если , и вверх в случае ),

•  — радиус Стокса частицы (м),

• g — ускорение свободного падения (м/с²),

• ρ_p — плотность частиц (кг/м³),

• ρ_f — плотность жидкости (кг/м³),

•  — динамическая вязкость жидкости (Па с).

Лобовое сопротивление

Лобовое сопротивление — сила, препятствующая движению тел в жидкостях и газах. Лобовое сопротивление складывается из двух типов сил: сил касательного (тангенциального) трения, направленных вдоль поверхности тела, и сил давления, направленных по нормали к поверхности. Сила сопротивления является диссипативной силой и всегда направлена против вектора скорости тела в среде. Наряду сподъёмной силой является составляющей полной аэродинамической силы.

Сила лобового сопротивления обычно представляется в виде суммы двух составляющих: сопротивления при нулевой подъёмной силе и индуктивного сопротивления. Каждая составляющая характеризуется своим собственным безразмерным коэффициентом сопротивления и определённой зависимостью от скорости движения.

Лобовое сопротивление может способствовать как обледенению летательных аппаратов (при низких температурах воздуха), так и вызывать нагревание лобовых поверхностей ЛА при сверхзвуковых скоростях ударной ионизацией.

Поток и форма препятствия	Профильное сопротивление	Сопротивление обшивки
	0 %	100 %
	~10 %	~90 %
	~90 %	~10 %
	100 %	0 %

Подъёмная сила — составляющая полной аэродинамической силы, перпендикулярная вектору скорости движения тела в потоке жидкости или газа, возникающая в результате несимметричности обтекания тела потоком. В соответствии с законом Бернулли, статическое давление среды в тех областях, где скорость потока более высока, будет ниже, и наоборот. Например, крыло самолета имеет несимметричный профиль (верхняя часть крыла более выпуклая), вследствие чего скорость потока по верхней кромке крыла будет выше, чем над нижней. Создавшаяся разница давлений и порождает подъёмную силу. Полная аэродинамическая сила — это интеграл от давления вокруг контура крыла.

где:

• Y — это подъёмная сила,

• P — это тяга,

•  — граница профиля,

• p — величина давления,

• n — нормаль к профилю

Коэффициент подъёмной силы

Коэффициент подъёмной силы — безразмерная величина, характеризующая подъемную силу крыла определённого профиля при известномугле атаки. Формула имеет вид:

где:

 — подъёмная сила (Н)

 — коэффициент подъёмной силы

 — весовая плотность воздуха на высоте полёта (кг/м³)

 — скорость набегающего потока (м/с)

 — характерная площадь (м²)

При расчетах по этой формуле важно не путать весовую и массовую плотность воздуха. Весовая плотность при стандартных атмосферных условиях (на уровне земли при температуре +15 С) равна =1.225 кг/м³. Но в аэродинамических расчетах часто используют массовую плотность воздуха, которая равна 0.125 кг*с²/м⁴. В этом случае подъемная сила Y получается не в ньютонах (Н), а в килограммах (кг). В книгах по аэродинамике не всегда имеются уточнения, о какой плотности и размерности подъемной силы идет речь, поэтому в спорных ситуациях нужно проверять формулы, сокращая единицы измерения.

Сверхзвукова́я ско́рость — скорость частиц вещества выше скорости звука для данного вещества или скорость тела, движущегося в веществе с более высокой скоростью, чем скорость звука для данной среды.

В аэродинамике часто скорость характеризуют числом Маха, которое определяется следующим образом: , где u — скорость движения потока или тела,  — скорость звука в среде. Звуковая скорость определяется как , где  — показатель адиабаты среды (для идеального n-атомного газа, молекула которого обладает  степенями свободы он равен ). Здесь  — полное число степеней свободы молекулы. При этом, количество поступательных степеней свободы . Для линейной молекулы количество вращательных степеней свободы , количество колебательных степеней свободы (если есть) . Для всех других молекул , .

При движении в среде со сверхзвуковой скоростью тело обязательно создаёт за собой звуковую волну. При равномерном прямолинейном движении фронт звуковой волны имеет конусообразную форму, с вершиной в движущемся теле. Излучение звуковой волны обуславливает дополнительную потерю энергии движущимся телом (помимо потери энергии вследствие трения и прочих сил).

Аналогичные эффекты испускания волн движущимися телами характерны для всех физических явлений волновой природы, например: черенковское излучение, волна, создаваемая судами на поверхности воды.