7 Переход в другую систему координат

Мы рассмотрели преобразования геометрических объектов, заданных в определенной декартовой системе координат. Но во многих случаях удобно рассматривать те же объекты в другой системе координат, поскольку их описание может стать более простым. Самый простой пример - задание координат параллелепипеда: проще всего это сделать в системе координат, совмещенной с одной из его вершин с осями, направленными вдоль ребер. В связи с этим остановимся на вопросе, как изменятся координаты точки при переходе от одной декартовой системы координат к другой.

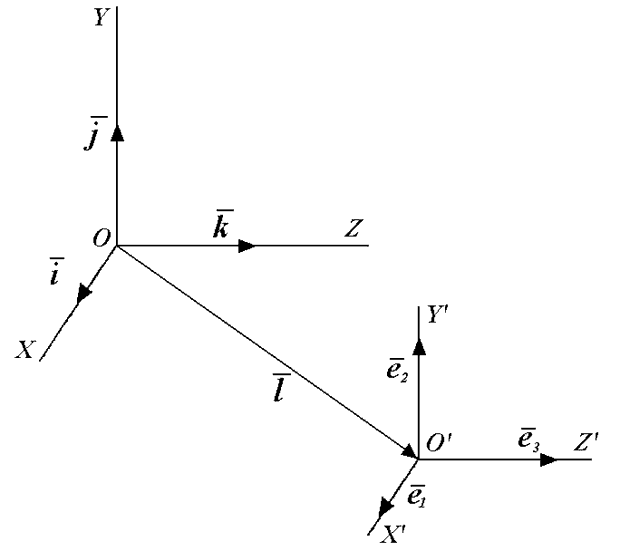
Рисунок 4.9.  Две системы координат в пространстве

Пусть единичные орты первой системы координат обозначаются , а оси координат -. Введем еще одну систему координат, единичные орты которой обозначим, а оси координат -. Эта система имеет свое начало координат и свои направления осей. Считаем, что в обеих системах координат орты образуют правую тройку (Рисунок 4.9).

Сначала рассмотрим ситуацию, когда точка совпадает с точкой. Векторыможно задать в первой системе координат, разложив их по векторам:

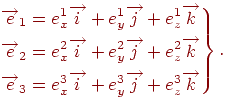
Если в первой системе точка имеет координаты, а во второй системе -, то, очевидно,

Умножая скалярно это соотношение на векторы , получим связь между значениями координат в разных системах:

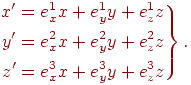
Эти соотношения можно записать в матричном виде

(4.11)

или в векторной записи

Предположим, что вторая система координат получена из первой путем поворота на угол относительно оси. Тогда

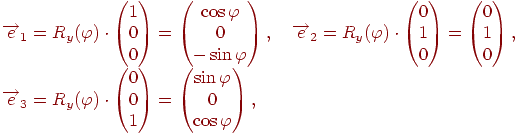
следовательно

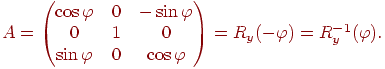
Таким образом, при поворотах системы координат новые координаты точек получаются путем умножения матрицы поворота на противоположный угол на вектор исходных координат.

Если новая система координат получена из старой путем сдвига на вектор , то очевидно, что новые координаты точки задаются формулами

Теперь можно рассмотреть композицию двух преобразований системы координат - переноса и вращения. Тогда координаты точек преобразуются по формуле

(4.12)

8 Задача вращения относительно произвольной оси

Вращение относительно произвольной оси также можно реализовать посредством умножения матрицы на вектор, но предварительно эту матрицу надо построить. Предположим, что прямая проходит через начало координат и задана единичным вектором , и требуется выполнить поворот точки на уголотносительно нее. Для этого воспользуемся следующим алгоритмом:

1. Совместим прямую с осью посредством поворота системы координат относительно осина угол, а затем поворота относительно осина угол.

2. Выполним поворот относительно оси на угол.

3. Выполним повороты системы сначала относительно оси на угол, а затем относительно осина угол(в обратном порядке по отношению к первым поворотам), тем самым возвращая ее в исходное положение.

Итоговая матрица преобразования, таким образом, является произведением нескольких матриц, а именно

Матрицы являются матрицами преобразования координат при поворотах системы координат, как было показано в предыдущем разделе. Определим сначала угол, который является углом между осьюи его проекцией векторана плоскость. Пусть- длина этой проекции. Тогда, (синус отрицателен, поскольку поворот идет от осик оси, т.е. в отрицательном направлении). После поворота системы координат новыми координатами векторабудут. Угол- это угол между векторамии, поэтому. Теперь мы можем выписать вид матриц преобразования координат для каждого шага алгоритма, учитывая то, что матрицы преобразования координат при повороте системы координат обратны по отношению к соответствующим матрицам вращения:

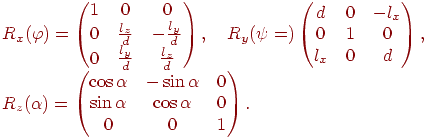
Нетрудно убедиться, что последовательное умножение матриц ина вектордадут в результате вектор, т.е. этот вектор действительно станет осью аппликат.

Остается только выписать окончательный вид матрицы (для сокращения записи введем следующие обозначения:):

(4.13)

Напомним, что являются направляющими косинусами прямой, относительно которой выполняется поворот. Нетрудно убедиться, что если в качестве осей вращения взять оси координат, то мы в точности получим формулы (4.10).

Рекомендации студентам по подготовке к лабораторной работе с указанием литературы

1. Плаксин. А.А., Лобанов А. В. Mental ray/iray. Мастерство визуализации в Autodesk. 3DS Max.– М.: ДМК Пресс, 2012. – 258 c.

2. Стиренко А. С. 3DS Max 2010-2011.– М.: ДМК Пресс, 2011. – 612 c.

3. Шешунова Г. Г. Основы компьютерной графики: учеб. пособ. / Г. Г. Шешунова. – Самара: Cамар. гос. техн. ун-т, 2009. – 138 c.

4. Ивнинг М., Шеве Дж. Аdobe PHOTOSHOP СS4 для фотогафов /Вершины мастерства Пер. с англ. Изд. «Русская редакция»,CПб.:-Петербург, 2010. – 400 с.

5. Гурский Ю. А., Гурская И. В., Жвалевский А. В. Компьютерная графика: PHOTOSHOP СS4, CORELDRAW Х4, ILLUSTRATOR СS4. Трюки и эффекты.–CПб.: Питер, 2009. – 800 с.

6. Гурский Ю. А., Жвалевский А. В. PHOTOSHOP СS4 Библиотека пользователя. – CПб.: Питер, 2009. – 608 с.

7. Климачева Т. Н. AutoCad 2008. Руководство конструктора/ Т. Н. Климачева. – М.: Эксмо, 2008. – 624 c

8. Мэрдок К. Л. 3ds max 9. Библия пользователя: Пер. с англ. – М.: Изд-во «Диалектика», 2007. -1376 с.

9. Бонни, Шон, Анзовин, Стив. Внутренний мир 3ds max 9. – М.: Издательский дом «Вильямс», 2007. 1072 - с.

Описание экспериментальных установок (лабораторного оборудования)

Лабораторная работа проводится в компьютерном классе на IBM-совместимых персональных ЭВМ.

Краткое содержание работы, выполняемой студентами в ходе занятия. Порядок проведения эксперимента, постановки опыта, снятия замеров и обработки данных эксперимента