Лабораторная работа № 6

МАТЕМАТИЧЕСКИЙ АППАРАТ ПроецированиЯ

Продолжительность 4 часа

Учебная и воспитательная цели:

Изучить математический аппарат проецирования. Прививать студентам навыки исследовательского подхода к изучению дисциплины. Воспитывать у студентов сознательное отношение к процессу обучения

Вопросы, подлежащие исследованию:

1. Математический аппарат проецирования.

Краткие теоретические или справочно-информационные материалы

1 МАТЕМАТИЧЕСКИЙ АППАРАТ ПРОЕЦИРОВАНИЯ

Для выполнения проективных преобразований будем использовать однородные координаты и матрицы преобразований, рассмотренные ранее в лекции 4. Проекция выполняется в системе координат наблюдателя.

Ортогональные проекции

Сначала рассмотрим математическое описание параллельных проекций как более простых. Случай, когда картинная плоскость перпендикулярна оси и задается уравнением(т.е. ортографическая проекция), фактически уже рассматривался в лекции 4, где был приведен вид матриц проекции на координатные плоскости.

Случай аксонометрической проекции сводится к последовательности преобразований, подобно тому как осуществлялся поворот в пространстве относительно произвольной оси. Пусть плоскость задается единичным вектором нормали и расстоянием от начала координат. Каноническое уравнение плоскости, таким образом, имеет вид

Вектор, направленный по нормали от начала координат до пересечения с плоскостью, есть

Координаты вектора единичной нормали являются ее направляющими косинусами.

Проецирование в пространстве однородных координат осуществляется следующей последовательностью шагов.

• Сдвиг на вектор с помощью матрицы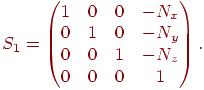

• 

• Поворот, совмещающий направление нормали с направлением оси . Как было показано в лекции 4, этот поворот можно реализовать в виде двух поворотов: первый (относительно оси) переводит нормаль в плоскость, а затем - поворот относительно осидо совмещения нормали с осью. Соответствующую матрицу вращения, являющуюся произведением двух матриц, обозначим.

• Проекция на плоскость с помощью матрицы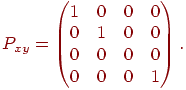

• 

• Поворот с помощью матрицы .

• Сдвиг на вектор с помощью матрицы

Полное преобразование, таким образом, определяется матрицей

Косоугольные проекции

Рассмотрим косоугольную проекцию на плоскость , при которой ортпереходит в вектор, т.е. направление проекции задается вектором. Такое преобразование в пространстве однородных координат можно задать с помощью матрицы

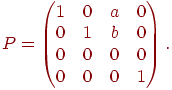
В проекции кавалье вектор переходит в вектор, а в кабинетной проекции - в вектор, причем в обеих проекциях.

Центральные проекции

Предположим, что центр проекции находится в точке , а картинная плоскость совпадает с плоскостью. Возьмем произвольную точку изображаемого объектаи определим ее проекцию на выбранную плоскость (Рисунок 9.7).

Рисунок 9.7.  Центральная проекция на плоскость XOY

Прямую, проходящую через точки и, зададим в параметрическом виде:

(9.1)

Теперь найдем точку пересечения этой прямой с картинной плоскостью. Она определяется из условия равенства нулю третьей координаты:

откуда определяем значение параметра , при котором точка прямой принадлежит координатной плоскости:

Подставляя это значение в формулу (9.1), мы получим координаты проекции точки :

(9.2)

Фактором, влияющим на перспективное изменение размеров, является наличие координаты в знаменателе. Чем ближе оказывается точка к центру проекции, тем больше знаменатель, а соответственно и координаты точки.

Мы будем рассматривать ситуацию, когда центр проекции лежит на оси , а сама ось направлена от наблюдателя к проекционной плоскости, т.е.. Тогда формулы (9.2) приобретают вид

(9.3)

В однородных координатах такое преобразование можно записать с помощью двух операций. Сначала умножаем матрицу проективного преобразования на исходную точку и получаем точку в четырехмерном пространстве:

(9.4)

Затем проецируем эту точку в пространство однородных координат путем деления на четвертую компоненту:

Посмотрим теперь, что происходит с пучком параллельных прямых под действием матрицы проекции. Пусть задан пучок прямых, параллельных вектору . Тогда параметрическое уравнение прямой, принадлежащей этому пучку, имеет вид

Из формулы (9.4) следует, что в результате проецирования получим множество точек

Переходя к однородным координатам и умножив числитель и знаменатель каждой дроби на , получим точкивида

Теперь в каждой компоненте вектора числитель и знаменатель поделим на :

Переходя к пределу при , получим точку

Таким образом, получаем, что после проецирования пучок параллельных прямых пересекается в точке схода . Понятно, что у каждого пучка своя точка схода. Если пучок прямых параллелен плоскости, т.е., то точка схода оказывается на бесконечности, а значит, прямые остаются параллельными.

Для построения перспективной проекции с несколькими точками схода используется матрица перспективного преобразования без проецирования:

Теперь точки пространства сначала подвергаются перспективному преобразованию, а затем осуществляется проекция.

Определим точки схода для прямых, параллельных осям координат. Для прямых результатом проективного преобразования будет множество точек, где. Приполучим точку с координатами. При проекции на плоскостьполучим точку. Пучок прямыхперейдет в, а точкой схода для него будет, которая при проецировании перейдет в точку, лежащую на оси. Аналогично для пучка прямых, параллельных оси, получим точку схода на оси. Эти три точки на плоскости являются главными точками схода.