2 Аналитическое представление кривых и поверхностей

Пусть на плоскости задана декартова система координат.

Кривая на плоскости - это геометрическое место точек , удовлетворяющих уравнению

(4.10)

где - функция двух переменных. Ясно, что далеко не каждая функция будет задавать линию. Так, например, уравнению

не удовлетворяет ни одна точка плоскости, а уравнению

удовлетворяет только одна точка .

Для аналитического представления кривой во многих случаях удобнее задавать кривую параметрическими уравнениями, используя вспомогательную переменную (параметр) :

(4.11)

где и- непрерывные функции на заданном интервале изменения параметра. Если функциятакова, что можно выразитьчерез, то от параметрического представления кривой легко перейти к уравнению (4.10):

Систему уравнений (4.11) можно записать в векторном виде:

Отрезок прямой представляет собой частный случай кривой, причем параметрическое представление его может иметь вид

или

Окружность радиуса с центром в точкеможет быть представлена параметрическими уравнениями

Перейдем к трехмерному пространству с заданной декартовой системой координат.

Поверхность в пространстве - это геометрическое место точек , удовлетворяющих уравнению вида

(4.12)

Так же как и в случае кривой на плоскости, не всякая функция описывает какую-либо поверхность. Например, уравнению

не удовлетворяет ни одна точка пространства. Поверхность также может быть задана в параметрическом виде, но в отличие от кривой для этого требуются две вспомогательные переменные (параметры):

(4.13)

Например, сфера радиуса с центром в точкеможет быть задана уравнением

либо же параметрическими уравнениями

Кривую в пространстве можно описать как пересечение двух поверхностей, т.е. с помощью системы уравнений

(4.14)

или параметрическими уравнениями вида

(4.15)

3 Пересечение луча с плоскостью и сферой

Прямая на плоскости и в пространстве является бесконечной в обе стороны. Лучом называется полупрямая, т.е. множество всех точек прямой, лежащих по одну сторону от заданной ее точки, называемой началом луча. Луч будем задавать в параметрическом виде, как это было описано в одном из предыдущих разделов. Пусть - направляющий вектор прямой, а- начальная точка. Тогда координаты точек луча будут определяться формулами

(4.8)

Будем считать, что направляющий вектор единичный, т.е. .

Сначала рассмотрим задачу о нахождении точки пересечения луча с плоскостью, заданной каноническими уравнением

(4.9)

Вектор нормали тоже будем считать единичным. Сначала надо определить значение параметра t, при котором луч пересекает плоскость. Для этого подставим координаты из формулы (4.8) в уравнение (4.9) и получим

откуда легко определить, что луч пересекает плоскость в точке со значением

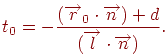
Очевидно, что такая точка существует только при условии . В свою очередь, эта величина обращается в нуль только в случае, когда векторыиортогональны друг другу.

Пусть теперь нам задана сфера с центром в точке и радиусом. Тогда уравнение сферы будет иметь вид

Подставив сюда координаты луча из уравнения (4.9), получим, что параметр, при котором луч пересекает сферу, должен удовлетворять квадратному уравнению

где . Определим корни этого уравнения. Если дискриминант, то корни существуют. Их может быть либо два, либо один. В первом случае имеем две точки пересечения, во втором - одну (луч касается сферы). Соответствующие значения параметра определяются соотношением