If (Условие, Выражение1, Выражение2)

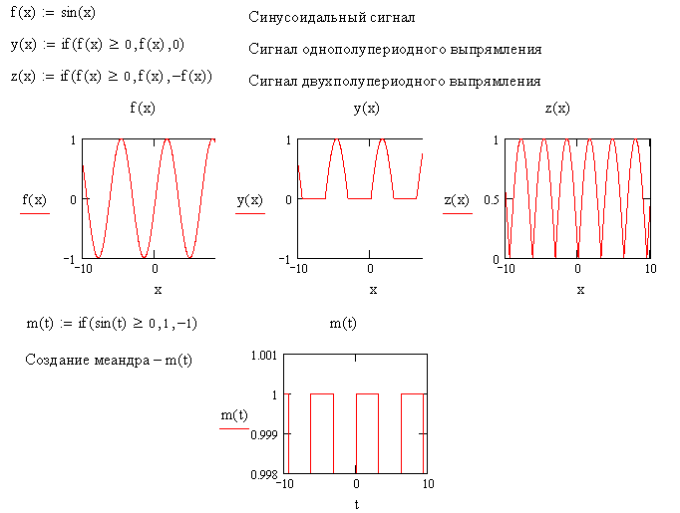
Если в этой функции условие выполняется, то будет вычисляться выражение 1, в противном случае – выражение 2. Эта функция широко распространена в языках программирования. С помощью функции с элементами сравнения можно моделировать другие функции логического или описывающие импульсивные сигналы различного вида. В качестве примера задана функция m(t) имитирующая прямоугольные периодические колебания. (Рис1)

Пример применения функции if

Рис 1

В системе Mactcad есть дополнительные функции сортировки – перестановка элементов векторов и матриц:

- sort (V) – сортировка элементов вектора в порядке возрастания их значений;

- csort (M,n) – перестановка строк матриц М таким образом, чтобы отсортированным оказался n-й столбец;

- rsort (M,n) – перестановка столбцов матриц М таким образом, чтобы отсортированным оказался n-я строка.

С этими функциями часто используется функция reverse (V) – изменение порядка расположения элементов вектора на противоположный (начиная с конца) (Рис2)

Примеры применения дополнительных векторных и матричных функций

Рис 2

Решение систем уравнений

MathCAD дает возможность решать также и системы уравнений. Результатом решения системы будет численное значение искомого корня.

Для решения системы уравнений необходимо выполнить следующее:

• Задать начальное приближение для всех неизвестных, входящих в систему уравнений. Mathcad решает систему с помощью итерационных методов.

• Напечатать ключевое слово Given. Оно указывает Mathcad, что далее следует система уравнений.

• Введите уравнения и неравенства в любом порядке. Используйте [Ctrl]= для печати символа =. Между левыми и правыми частями неравенств может стоять любой из символов <, >, ≤, и ≥.

Чтобы решить систему уравнений в символьном виде, необходимо выполнить следующее:

• Напечатать ключевое слово Given.

• Напечатать уравнения в любом порядке ниже слова Given. Удостоверьтесь, что для ввода знака = используется булево равенство ([Ctrl]=).

• Напечатать функцию Find, соответствующую системе уравнений.

• Нажать [Ctrl]. (клавиша CTRL, сопровождаемая точкой). Mathcad отобразит символьный знак равенства →.

• Щелкнуть мышью на функции Find.

Рис 3

Find(var1,var2, …) значения var1, var2, …, дающие точные решения системы уравнений в блоке, объявленном директивой Given (число возвращаемых значений равно числу аргументов),который помимо решаемой системы уравнений, может содержать условия ограничения.

Given – ключевое слово, открывающее блок решения систем уравнений (в котором обычно используются функции Find, Minerr, Maximize и Minimize)

Решить систему линейных уравнений:

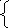4x₁ +x₂ + x₃+3x₄=25

3x₁ – x₂+3x₃=16

2x₁ – 2x₂ + 3x₄=– 4

x₁+2x₂ – x₃ + 2x₄=4

Матричным способом X:=A^-1  B, где А- матрица, составленная из коэффициентов а11… а33, В – вектор свободных членов b1, b2, b3, X – вектор корней x1, x2, x3;

• С помощью встроенной функции lsolve(А,В).

Проверить результаты решения непосредственной подстановкой полученных корней х1, х2, х3 в одно из заданных уравнений.