1.Нормирование по частоте

Нормирование производим относительно граничной частоты полосы пропускания , .

Соответственно ,, и.

Рисунок 1.1 – Характеристика технических требований ФНЧ.

2. Аппроксимация частотной характеристики рабочего ослабления фильтра по Чебышеву.

В качестве аппроксимирующих удобно использовать полиномиальные функции, среди которых наиболее широкое применение имеют полиномы Баттерворта и Чебышева.

При выборе полинома Чебышева в качестве аппроксимирующего функция фильтрации определяется выражением:

, где .

–коэффициент неравномерности рабочего ослабления в полосе пропускания.

Рабочее ослабление определяется как: .- полином Чебышева, определяемый рекуррентной формулой,n- порядок фильтра:

Округляя в большую сторону, возьмем , тогда.

Аппроксимация по Чебышеву получила название равноволновой.

Сформируем рабочую передаточную функцию:

.

С другой стороны модуль рабочей передаточной функции можно представить как:

.

Таким образом:

,т.е. ,

–полином Гурвица.

Решая уравнение , определим корни полинома Гурвица: , =0,2314

Имеем:

Рисунок 2.1 – Изображение корней уравнения на комплексной плоскости

Сформируем рабочую операторную передаточную функцию :

Подставляя , определим рабочее ослабление как:.

Выполним проверку функции на частотах:,,.

Аппроксимированное рабочее ослабление удовлетворяет техническим требованиям.

Рисунок 2.2 – График рабочего ослабления ФНЧ

Рисунок 2.3 – График рабочего ослабления ФНЧ в ПП

Аппроксимация по Чебышеву даёт большую крутизну нарастания характеристики рабочего ослабления, чем аппроксимация по Баттерворту. Из данного расчёта видно, что для фильтра Чебышева на частоте рабочее ослаблениечто соответствует норме, а на частотерабочее ослабление, что также соответствует норме. Крутизна нарастания характеристики определяется порядком фильтра. Чем выше порядок цепи, тем круче происходит нарастание рабочего ослабления. Аппроксимация по Чебышеву получила название равноволновой. Число экстремумов в ПП, включая граничные частоты, зависит от технических требований к фильтру и равноn+1.

3. Реализация схемы фнч по Попову.

На данном этапе по найденной ранее функции необходимо получить схему фильтра нижних частот.

Существует несколько способов реализации электрических фильтров: по Дарлингтону, ускоренный метод реализации симметричных и антиметричных фильтров Попова, реализация по каталогу нормированных схем, структурная параметрическая и т.д. Согласно варианту будем проводить реализацию электрического фильтра по ускоренному методу Попова. Данный вид реализации основан на формировании функции по . Тогда получение схемы нагруженного фильтра можно свести к реализации двухполюсника путем разложения функции в цепную дробь (по Кауэру).

Так как порядок фильтра нечетный, необходимо выполнить следующие действия:

1. Для каждой пары комплексно-сопряженных корней полиномапередаточной функциисоставим элементарный сомножитель:

.

2. Сформируем полином как произведение элементарных сомножителей с нечетными индексами:

.

3. Сформируем полином как произведение элементарных сомножителей с четными индексами:

.

4. Составим функцию :

, где .

5. Разложим полученную функцию в цепную дробь по Кауэру и построим нормированную схему правой части фильтра.

.

Нормированные значения ёмкостей и индуктивностейбудут равны:

, , ,.

Построим нормированную схему правой половины фильтра:

^,,.

Рисунок 3.1. – Нормированная схема правой половины фильтра.

Построим нормированную схему левой половины фильтра, исходя из условий симметрии .

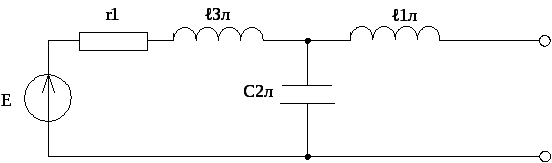
Рисунок 3.2. – Нормированная схема левой половины фильтра.

После объединения левой и правой половин, получим полную нормированную схему фильтра (рисунок 3.4).

l1, l3, l5 подчеркнул вопросом

Рисунок 3.3. – Схема фильтра, полученная после объединения левой и правой частей.

Получим дуальную схему фильтра:

Рисунок 3.7. – Дуальная схема фильтра.

с1, с3 тоже под вопросом

В общем случае, из двух выше приведённых схем для дальнейшего исследования выбирается более экономичная (с меньшим количеством индуктивностей в исходном фильтре). В данном примере выберем схему с источником тока.