6. Разбиение множества на классы. Классификация

В процессе изучения предметов и явлений окружающего мира мы постоянно сталкиваемся с классификацией. Классификация широко используется в биологии, химии, математике, языке и многих других науках. Она облегчает процесс усвоения знаний.

Классификация в любой области человеческой деятельности связана с разбиением множества на подмножества (классы). Например, классификация частей речи, членов предложения, чисел, геометрических фигур и так далее.

Полученные подмножества должны обладать следующими свойствами:

1) они не должны быть пустыми;

2) не должны содержать общих элементов;

3) объединение всех подмножеств должно равняться самому множеству.

Определение: Классификацией или разбиением множества на классы называется представление этого множества в виде объединения непустых попарно непересекающихся своих подмножеств.

Для примера рассмотрим классификацию с помощью двух свойств.

Пусть U — множество студентов юридического факультета ИУБ и П, свойство α - «быть отличником», свойство β - «быть спортсменом». С помощью указанных свойств можно выделить следующие подмножества:

А — множество отличников;

— множество не отличников;

В — множество спортсменов;

— множество не спортсменов.

М

ножество U в этом случае оказывается разбитым на следующие четыре класса (подмножества):

I — множество отличников-спортсменов;

II — множество отличников - не спортсменов;

III — множество не отличников - спортсменов;

IV — множество не отличников - не спортсменов;

Рис. 2

Можно доказать, что если n — число свойств, то максимальное число классов в разбиении равно 2ⁿ.

7. Число элементов объединения и разности двух конечных множеств

Пусть A и B — конечные множества. Число элементов множества A условимся обозначать символом m(A) и называть численностью множества A.

Определим численность объединения множеств A и B.

Если множества A и B не пересекаются (см. рис. 1а), то m(AB) = m(A) + m(B). Таким образом, численность объединения конечных непересекающихся множеств равна сумме численностей этих множеств.

Если множества A и B пересекаются (см. рис. 1б), то в сумме m(A) + m(B) число элементов пересечения AB содержится дважды: один раз в m(A), а другой — в m(B). Поэтому, чтобы найти численность объединения m(AB) , нужно из указанной суммы вычесть m(AB). Таким образом:

m(AB) = m(A) + m(B) - m(AB)

Определим теперь численность разности множеств A и B.

Если множества A и B не пересекаются (см. рис. 1а), то A \ B = A, и поэтому m(A\B) = m(A).

Если множества A и B пересекаются (см. рис. 1б), то m(A\B) = m(A) - m(AB).

Если В  А (см. рис. 1в), то AB = B, и, следовательно, m(A\B) = m(A) - m(B).

8. Примеры решения задач

Задача 1. Каждый студент первого курса обязан изучать хотя бы один иностранный язык. На юридическом факультете изучаются либо английский, либо немецкий язык. Из 94 первокурсников юридического факультета 76 человек изучают английский язык, 34 – изучают немецкий. Сколько студентов изучают два языка?

Решение. Обозначим А – множество студентов, изучающих английский язык; В – множество студентов, изучающих немецкий язык. Множество всех первокурсников равно АВ. Множество, изучающих два языка AB. Воспользуемся формулой

m(AB) = m(A) + m(B) - m(AB).

Из условия задачи m(A)=76, m(B)=34, m(AB) =94. Поэтому

m(AB)= 76+34-94=16.

Задача 2. В одном из городов Украины часть жителей говорит только по-русски, часть – только по-украински, часть говорит на обоих языках. Известно, что 90% жителей говорит по-русски, а 80% - по-украински. Какой процент жителей говорит на обоих языках? Какой процент говорит только по-русски? Какой процент говорит только по-украински?

Решение. Введем ряд обозначений. Пусть N – множество жителей, говорящих по-русски, а K – по-украински. По условию задачи m(N) = 90%, m(K) = 80%, а m(NK) = 100% - это общее число жителей. Процент двуязычных жителей m(NK) может быть определен из соотношения

m(NK) = m(N) + m(K) -m(NK)

100%=90%+80%- m(NK)

m(NK)=90%+80%-100%=70%.

Множества одноязычных жителей определяются следующими выражениями:

Русскоязычные - N\(NK), говорящие только по-украински - K\(NK). Поскольку в обоих случаях пересечение (NK) является подмножеством множеств N и K, то количество одноязычных жителей может быть получено по формулам

m(N\(NK))= m(N)- m(NK)=90%-70%=20%

m(K\(NK))= m(K)- m(NK)=80%-70%=10%

Задача 3. Итоговое рейтинговое задание по курсу «Математика и информатика» содержало три задания: по MS Office, по математике и по Справочной правовой системе (СПС). Результаты проверки задания у 40 студентов представлены ниже.

Выполнены задания	Количество выполнивших	Выполнены задания	Количество выполнивших
MS Office	20	MS Office и СПС	7
СПС	18	MS Office и математика	8
Математика	18	СПС и математика	9

Известно также, что ни одного задания не выполнили трое. Сколько студентов выполнили все три задания? Сколько студентов выполнили ровно два задания?

Решение. Введем обозначения: N– множество студентов, выполнивших задание по MS Office; K – выполнивших задание по СПС; P – выполнивших задание по математике; x – число студентов, выполнивших все три задания. Дадим графическое представление рассматриваемых множеств (Рис. 3).

Рис. 3

Из рисунка можно отметить следующие данные: (7-x) – число студентов, выполнивших задания MS Office и СПС, но не по математике; (8-x) - число студентов, выполнивших задания MS Office и математике, но не по СПС, (9-x) – по СПС и математике, но не по MS Office.

Если n, k, p – количество студентов, выполнивших только одно задание соответственно по MS Office, СПС и математике, то можно записать следующие выражения:

m(N)=20=16+n-x; m(K)=18=15+k-x; m(P)=18=17+p-x,

в результате решения которых получим следующие соотношения:

n=4+x; k=3+x; p=1+x.

Всего в рейтинге участвовало 40 студентов, трое не выполнили ни одного задания, это означает, что, по крайней мере, одно задание выполнили 37 студентов.

Множество студентов, выполнивших, по крайней мере, по одному заданию - NKP.

m(NKP) = 37. В соответствии с рис.3 это выражение будет равно:

m(NKP) = n+k+p+24-2x,

подставив в него выражения n, k и p через x, получим

4+x+3+x+1+x+24-2x=37

x=37-32=5.

Таким образом, число студентов, выполнивших все три задания равно 5.

Для определения количества студентов, выполнивших ровно два задания, из рисунка 3 получается следующее выражение

9-x+8-x+7-x=24-3x=24-15=9.

Задача 4. В штучном отделе магазина посетители обычно покупают либо один торт, либо одну коробку конфет, либо один торт и одну коробку конфет, В один из дней было продано 57 тортов и 36 коробок конфет. Сколько было покупателей, если 12 человек купили и торт, и коробку конфет?

Решение.

Обозначим через T множество покупателей, купивших торт, а через К – множество покупателей коробки конфет. Тогда отношение между этими множествами может быть проиллюстрировано следующей диаграммой (Рис.4).

Тогда множество всех покупателей определяется, как объединение вышеуказанных множеств Т  К. А множество покупателей, сделавших две покупки, получается в результате пересечения тех же множеств Т  К.

Их количество согласно условию задачи m(Т К) = 12.

Согласно теории m(Т К)=m(Т) + m(К) - m(Т  К).

Подставив в эту формулу данные из условия задачи, получим m(Т К)= 57 + 36 – 12 = 81.

Задача 5. Каждый из студентов 1 курса в зимние каникулы ровно два раза был в театре на разных спектаклях, при этом спектакли А, В и С видели соответственно 50, 24 и 46 студентов. Сколько студентов на 1 курсе? Сколько из них видели спектакли А и В, А и С, В и С?

Решение.

Обозначим через S множество всех студентов первого курса, а через А, В и С соответственно множества студентов, посетивших спектакли А, В и С. С учетом введенных обозначений нам необходимо определить m(S), m(АВ), m(АС) и m(ВС). Соотношения между подмножествами данной задачи показано на схеме (Рис. 5).

Поскольку каждый студент посетил ровно два спектакля справедливо следующее соотношение m(S)=(m(A) + m(B) + m(C)) / 2 = (50 + 24 + 46) / 2 = 60. То есть, число студентов первого курса равно 60.

Поскольку каждый студент посетил два разных спектакля, то любой студент попадает либо в множество А, либо в множество В. Поэтому объединение этих множеств дает множество всех студентов, то есть S = AB. Если рассмотреть пары множеств А и С, В и С, то рассуждая аналогичным образом мы придем к справедливости соотношений

S = AС и S = ВС.

Согласно теории m(А  В)=m(А) + m(В) - m(А  В).

Поэтому m(АВ)=m(А) + m(В) - m(А  В) = m(А) + m(В) - m(S) = 50 + 24 –60 =14.

Аналогично могут быть определены m(А  С) и m(В  С).

m(А  С)=m(А) + m(С) - m(А  С) = m(А) + m(С) - m(S) = 50 + 46 –60 =36.

m(В  С)=m(В) + m(С) - m(В  С) = m(В) + m(С) - m(S) = 24 +46 –60 =10.

Задача 6. Преподаватель решил узнать, кто из 40 студентов читал книги А, В и С. Результаты опроса оказались таковы: книгу А читало 25 человек, книгу В — 22, книгу С — также 22. Книгу А или В читали 33 студента, А или С — 32, В или С — 31; все три книги прочли 10 студентов. Сколько студентов прочли только по одной книге? Сколько студентов не читали ни одной из этих трех книг?

Решение.

Обозначим через А, В и С соответственно множества студентов, читавших книги А, В и С. Соотношение между перечисленными множествами показано на схеме (Рис.6).

Из условий задачи имеем: m(A) =25, m(B) =22, m(C) = 22,

m(А  В) =33, m(А  С) = 32, m(В  С) =31 и m(А  В  С) =10.

Если обозначить через D множество студентов, прочитавших, по крайней мере, одну из трех книг, то, очевидно, что для определения количества членов этого множества справедливо следующее выражение

m(D) = m(A) + m(B) + m(C) –m(АВ) - m(АС) - m(ВС) + m(АВС ).

Если обозначить через Е множество студентов, прочитавших две или три книги, то, очевидно, что для определения количества членов этого множества справедливо следующее выражение m(Е) =m(А  В) + m(А  С) + m(В  С) – 2* m(А  В  С ).

К1 - количество студентов, прочитавших только по одной книге, может быть найдено по формуле К1 = m(D) – m(E), а число студентов, не прочитавших ни одной книги K0 = 40 – m(D).

Таким образом для определения всех искомых величин нам необходимо определить m(А  В), m(А  С) и m(В  С).

Согласно теории m(А  В)=m(А) + m(В) - m(А  В) = 25 + 22 – 33 = 14,

m(А  С)=m(А) + m(С) - m(А  С) = 25 + 22 – 32 = 15,

m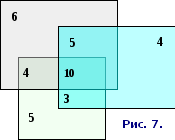(В С)=m(В) + m(С) - m(В  С) = 22 + 22 – 31 = 13.

Подставим полученные результаты в вышеприведенные формулы

m(D) = m(A)+ m(B) + m(C) –m(АВ) - m(АС) - m(ВС) + m(АВС ) =

25 + 22 + 22 –14 – 15 –13 +10 = 37,

m(Е) =m(АВ) + m(АС) + m(ВС) – 2* m(АВС ) = 14 + 15 + 13 – 2 * 10 = 22,

К1=m(D) – m(E) =37 – 22=15, K0 = 40 – m(D) =40 – 37= 3.

Если провести разбиение множества всех студентов, прочитавших хотя бы одну книгу на классы, то есть непустые и непересекающиеся подмножества, то количество элементов в каждом классе может быть показано на схеме (Рис. 7).

Задача 7. В течение недели в кинотеатре демонстрировались фильмы А, В и С. Из 40 студентов, каждый из которых просмотрел либо все три фильма, либо один из трех, фильм А видели 13, фильм В — 16, фильм С — 19. Найти, сколько студентов просмотрели все три фильма.

Решение.

Обозначим через А, В и С соответственно множества студентов, посмотревших фильмы А, В и С. Соотношение множеств данной задачи показано на диаграмме (Рис. 4).

Из условия задачи имеем: m(A)=13, m(B) =16, m(C) = 19,

m(А  В  С) = 40.

Требуется определить m(А  В  С).

Из соотношения множеств, отображенного на диаграмме, можно заключить, что справедливо следующее равенство

m(А  В  С) = m(A) + m(B) + m(C) –2* m(А  В  С).

Поэтому m(АВС) = (m(A) + m(B) + m(C) - m(АВС))/2 = (13 + 16 + 19 – 40) / 2 = 4.