
- •Оглавление
- •Введение
- •Глава 1. Классическое и геометрическое определения вероятности
- •1.1.Классическое определение вероятностей. Задачи
- •1.2.Геометрическая вероятность
- •1.3. Задачи для самостоятельного решения
- •Глава 2. Условная вероятность. Теоремы умножения и сложения вероятностей
- •2.1. Операции над событиями. Независимость событий
- •2.2. Условная вероятность
- •2.3. Теоремы умножения и сложения вероятностей
- •2.3. Задачи для самостоятельной работы
- •Глава 3. Формула полной вероятности и формула Байеса
- •Глава 4. Схема независимых испытаний Бернулли. Предельные теоремы в схеме Бернулли
- •Глава 5. Дискретные случайные величины и их характеристики
- •5.1. Дискретные случайные величины
- •5.2. Задачи для самостоятельной работы.
- •Глава 6. Непрерывные случайные величины и их характеристики
- •6.1. Непрерывные случайные величины и их числовые характеристики
- •Глава 7. Элементы математической статистики
- •7.2. Доверительное оценивание
- •1. Доверительный интервал для неизвестного математического ожидания нормального распределения (при известной дисперсии)
- •2. Доверительный интервал для неизвестного математического ожидания нормального распределения (при неизвестной дисперсии)
- •3. Доверительный интервал для неизвестного среднего квадратического отклонения нормального распределения
- •7.4. Задачи для самостоятельной работы
- •Список литературы
Глава 5. Дискретные случайные величины и их характеристики
Пусть
![]()
![]() ,
,![]() -
вероятностное пространство,
-
вероятностное пространство,![]() –множество
действительных чисел.
–множество
действительных чисел.
Определение.
Случайной величиной называется
действительная функция
![]() ,
(
,
(![]() ) такая, что для каждого действительного
) такая, что для каждого действительного![]()
![]() .
.
Напомним, что
![]() –
–![]() -алгебра
событий, то есть
-алгебра
событий, то есть![]() – некоторое событие вероятностного
пространства.
– некоторое событие вероятностного
пространства.
Определение. Функция
![]() (5.1)
(5.1)
называется функцией
распределения вероятностей случайной
величины
![]() .
.
Свойства функции распределения вероятностей:
1.
![]() для любого
для любого
![]() ;
;
2.
![]() -
неубывающая, непрерывная слева;
-
неубывающая, непрерывная слева;
3.
![]()
![]() т.е.
т.е.![]() ,
,![]() ;
;
4.
![]() .
.
Определение.
Случайные величины
![]() и
и![]() называются независимыми, если при любых
действительных
называются независимыми, если при любых
действительных![]() и
и![]() имеет место
имеет место
![]() .
.
К основным числовым характеристикам случайных величин относят математическое ожидание, дисперсию и среднее квадратическое отклонение.
Определение.
Математическим ожиданием дискретной
случайной величины
![]() называется число
называется число
![]() , (5.2)
, (5.2)
(при условии, что
ряд сходится). Здесь
![]() –значения
случайной величины
–значения
случайной величины![]() ,
,![]() –вероятность, с которой случайная
величина
–вероятность, с которой случайная
величина![]() принимает значение
принимает значение![]() .
.
Свойства математического ожидания.
1. Если
![]() ,
то
,
то![]() .
Иначе
.
Иначе![]() ,
где
,
где![]() .
.
2.
![]() ,
где
,
где![]() .
.
3.
![]() .
.
4. Если случайные
величины
![]() и
и![]() независимы, то
независимы, то![]() .
.
Определение.
Математическим ожиданием дискретной
случайной величины
![]() называется число
называется число
![]() , (5.3)
, (5.3)
(при условии, что ряд сходится).
Определение.
Дисперсией случайной величины
![]() называется число
называется число
![]() , (5.4)
, (5.4)
Свойства дисперсии.
0.
![]() .
.
1. Если
![]() ,
то
,
то![]() .
Иначе
.
Иначе![]() ,
где
,
где![]() .
.
2.
![]() ,
где
,
где![]() .
.
3. Если случайные
величины
![]() и
и![]() независимы, то
независимы, то
![]() .
.
4.
![]() .
.
Определение.
Средним квадратическим отклонением
случайной величины называют величину
![]() .
.
5.1. Дискретные случайные величины
Опыт состоит из трех независимых бросаний монеты, при каждом из которых герб совпадает с вероятностью
 .
Для случайного числа появления герба
построить: а) ряд распределения; б)
функцию распределения; в) вычислить
числовые характеристики.
.
Для случайного числа появления герба
построить: а) ряд распределения; б)
функцию распределения; в) вычислить
числовые характеристики.В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения случайной величины
 –
числа стандартных деталей среди
отобранных. Построить функцию
распределения вероятностей и ее график.
Вычислить числовые характеристики.
–
числа стандартных деталей среди
отобранных. Построить функцию
распределения вероятностей и ее график.
Вычислить числовые характеристики.В партии 10% нестандартных деталей. Наудачу отобраны четыре детали. Написать ряд распределения числа нестандартных деталей среди отобранных четырех.
Случайные величины
 и
и независимы, причем
независимы, причем ,
, ,
, ,
, .
Найти
.
Найти и
и , если: а)
, если: а)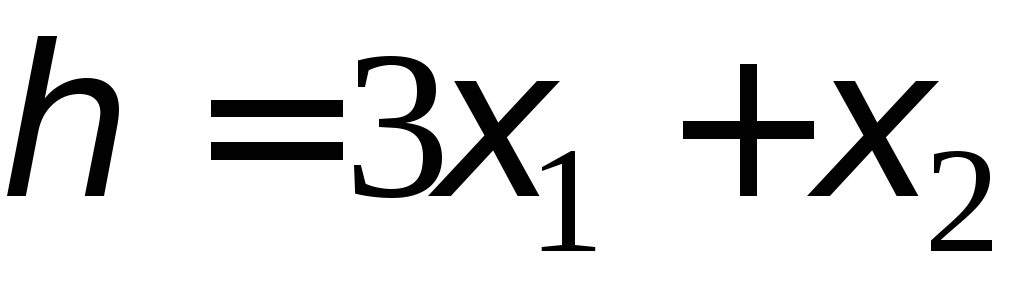 ; б)
; б) в)
в)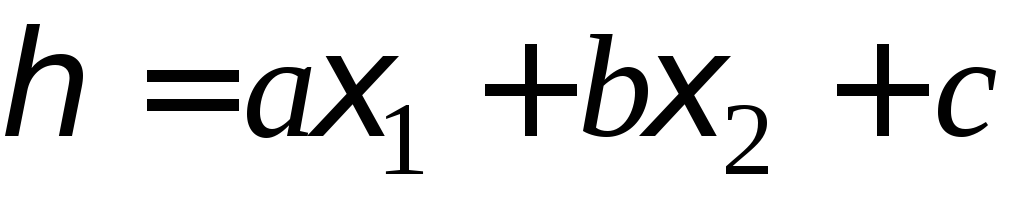 ,
где
,
где ,
, ,
, – постоянные величины.
– постоянные величины.Дан ряд распределения дискретной случайной величины
 :
:
|
а) |
|
-2 |
-1 |
0 |
1 |
б) |
|
-3 |
1 |
3 |
4 |
|
|
|
0.1 |
0.2 |
0.2 |
0.4 |
|
|
0.3 |
0.2 |
0.1 |
0.4 |
Требуется: 1)
записать функцию распределения
вероятности величины
![]() и построить ее график; 2) построить ряд
распределения случайной величины
и построить ее график; 2) построить ряд
распределения случайной величины
![]() ;
3) определить числовые характеристики
случайной величины.
;
3) определить числовые характеристики
случайной величины.
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины, заданной законом распределения:
|
а) |
|
3 |
5 |
7 |
9 |
б) |
|
0 |
1 |
2 |
|
|
|
0.4 |
0.3 |
0.2 |
0.1 |
|
|
0,3 |
0,5 |
0,2 |
