
n1
.doc|
1.Электрические заряды и их взаимодействие. Закон кулона. Вектор напряженности электрического поля. Все тела в природе способны электризоваться, т.е. приобретать электрический заряд. Наличие электрического заряда проявляется в том, что заряженное тело взаимодействует с другими заряженными телами. Имеются 2 вида электрических зарядов, условно называемых положительными и отрицательными. Заряды одного знака отталкиваются, заряды разных знаков притягиваются. Электрический заряд является свойством некоторых элементарных чатиц, например электрон имеет отрицательный заряд –e, протон – положительный заряд +e, нейтрон – заряд равный нулю. Заряд элементарных частиц одинаковый по величине и называется элементарным зарядом
|
. Электрические заряды входят в состав атомов и молекул любого вещества. Обычно частицы, несущие отрицательный и положительный заряды присутствуют в веществе в одинаковом количестве (молекула нейтральна). Если создать избыток положительно заряженных частиц в теле, то тело станет положительно заряженным (положительно заряженный ион), и наоборот, если отрицательно заряженных частиц больше, то будем иметь отрицательно заряженное тело ( отрицательный ион). В 1785 году Кулон экспериментально установил закон взаимодействия точечных зарядов. Точечным зарядом называется заряженное тело, размерами которого можно пренебречь по сравнению с расстояниями от этого тела до других тел, несущих электрический заряд. |
Кулон с помощью крутильных весов измерял силу взаимодействия двух заряженных шариков в зависимости от величины зарядов на них и от расстояния между ними.Закон: Сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними. Направление силы совпадает с направлением прямой соединяющей заряды.
|
||||||||||||||||
|
Если
имеется система зарядов : заряд qa
и еще n
зарядов, то равнодействующая сила с
которой действует заряд qa
определяется формулой
|
В
симтеме единиц СГСЭ ( абсолютная
электростатическая система единиц:
грамм, см, секунда, для заряда – СГСЭ
абсолютная электростатическая единица
заряда k=1 и закон кулона имеет вид
В
системе единиц СИ коэффициент
пропорциональности в законе Кулона
равен
|
Напряженность электростатического поля Всякий заряд изменяет свойства окружающего его пространства – создает в нем электрическое поле. Это поле проявляется в том, что помещенный в какую-либо его точку Электрический
заряд испытывает воздействие силы.
Взаимодействие между заряждами
осуществляется через электрическое
поле. Будем вносить пробные заряды в
поле неподвижного точечного заряда
и измеряя силы, действующие на пробный
заряд было установлено что отношение
|
||||||||||||||||
|
Величину
Направление вектора напряженности E – вдоль радиальной прямой, проходящей через заряд и данную точку поля, от заряда, если он положителен, и к заряду, если он отрицателен.
|
2. Принцип суперпозиции электрических полей. Напряженность электрического поля, создаваемая системой точечных зарядов, непрерывным распределением зарядов. Поле диполя, бесконечной прямолинейной однородно заряженной нити. Напряженность электростатического поля Всякий заряд изменяет свойства окружающего его пространства – создает в нем электрическое поле. Это поле проявляется в том, что помещенный в какую-либо его точку Электрический заряд испытывает воздействие силы. Взаимодействие между заряждами осуществляется через электрическое поле. Будем вносить пробные заряды в поле неподвижного точечного заряда и измеряя силы, действующие на пробный заряд было |
установлено
что отношение
|
||||||||||||||||
|
На
всякий точечный заряд q в точке поля
с напряженностью E будет действовать
сила
|
Напряженность электрического поля от нескольких зарядов находится по правилу векторного сложения полей. Принцип суперпозиции позволяет вычислять напряженность поля любой системы зарядов. Разбив протяженные заряды на достаточно малые доли, любую систему можно свести к совокупности точечных зарядов. Напряженность поля, образованного заряженной бесконечно протяженной плоскостью
Напряженность поля, образованного бесконечно длинной нитью
|
Диполем называется система двух разноименных зарядов одинаковых по величине +q и –q, расстояние l между которыми значительно меньше расстояния до тех точек системы, в которых определяется поле системы. Прямая, проходящая через оба заряда, называется осью диполя.
|
||||||||||||||||
|
Положив θ=π/.2, получим напряженность поля на оси диполя
Характерным
для напряженности поля является то
обстоятельство, что она убывает с
расстоянием от диполя как
|
3. Силовые линии напряженности электрического поля. Поток вектора напряженности электрического поля. Теорема Остроградского-Гаусса, имеры ее применения (поле, создаваемое однородной бесконечной плоскостью). Электрическое поле можно описывать, указав для каждой точки величину и направление вектора E. Электрическое поле можно описать с помощью линий напряженности электрического поля. Линии напряженности проводят таким образом, чтобы касательная к ним в каждой точке совпадала с направлением вектора E. |
Густота линий выбирается таким образом, чтобы количество линий, пронизывающих единицу поверхности, перпендикулярной к линиям площадки, было равна числовому значению вектора E. Тогда по картине линий вектора E можно судить о величине и направлении напряженности в разных точках пространства. Поток вектора.
Величина
|
||||||||||||||||
|
В случае замкнутых поверхностей принято вычислять поток «вытекающий» наружу, следовательно нормаль всегда подразумевается направленная наружу (внешняя нормаль).
Дивергенцией
называется величина
|
то
разделив это выражение на
Теорема Остроградского-Гаусса
Зная
дивергенцию вектора в каждой точке
пространства, можно вычислить поток
этого вектора через любую замкнутую
поверхность конечных размеров.
Соотношение
|
Силы, действующие на заряд q являются консервативными, т.е. работа этих сил на любом замкнутом контуре равна нулю:
|
||||||||||||||||
|
Согласно
теореме Стокса (
Теорема Гаусса Поток
вектора E
равен
|
В силу принципа суперпозиции напряженность E, создаваемая всеми зарядами, равна сумме напряженностей, создаваемых каждым зарядом в отдельности. Поэтому
|
В данном случае физически малый объем должен быть мал, чтобы плотность была одинаковой, но и не слишком мал, чтобы не появилась дискретность заряда. Зная плотность заряда в каждой точке пространства, можно вычислить суммарный заряд
|
||||||||||||||||
|
Теорема
Гаусса позволяет вычислять напряженность
полей. Поверхностная плотность
определяется по формуле
Поле бесконечной заряженной плоскости. Пусть поверхностная плотность заряда во всех точках одинакова и равна σ. Будем считать заряд положительным. Из соображений симметрии вытекает, что напряженность поля в любой точке имеет направление перпендикулярное к плоскости.
|
Далее
очевидно, что в симметричных относительно
плоскости точках напряженность поля
одинакова по величие и противоположна
по направлению. Пусть цилиндрическая
поверхность с образующими перпендикулярными
к плоскости и основаниями величины
|
4. Работа сил электрического поля при перемещении заряда. Теорема о циркуляции вектора напряженности электростатического поля.
Рассмотрим
поле, создаваемое неподвижным зарядом
q. В любой точке этого поля на точечный
заря действует сила Кулона
|
||||||||||||||||
|
Работа
равна
|
.
Интеграл может быть взят по любой Лии,
соединяющей точки 1 и 2. Для обхода по
замкнутому контуру
Теорема о циркуляции. Силы, действующие на заряд q являются консервативными, т.е. работа этих сил на любом замкнутом контуре равна нулю:
|
Т.о.
циркуляция вектора напряженности по
любому замкнутому контуру равна нулю.
Возьмем произвольную поверхность,
опирающуюся на контур Г,
для
которого вычисляется циркуляция.
Согласно теореме Стокса (
|
||||||||||||||||
|
5. Потенциал электростатического поля, разность потенциалов. Потенциал точечного заряда.
Рассмотрим
поле, создаваемое неподвижным зарядом
q. В любой точке этого поля на точечный
заря действует сила Кулона
|
Работа
равна
Будем вносить в поле разные пробные заряды. Разные пробные заряды будут обладать в одной и той же точке разными потенциальными энергиями. |
Однако
отношение потенциальной энергии к
пробному заряду
|
||||||||||||||||
|
Заряд
находящийся в точке поле с потенциалом
φ обладает потенциальной энергией
|
Следовательно, потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки на бесконечность. Единицы потенциала 1В = 1Дж/1Кл. Связь между напряженностью поля и его потенциалом
Напряженность
поля точечного заряда
|
6. Связь вектора напряженности электрического поля с потенциалом. Эквипотенциальные поверхности. Электрическое поле можно описать либо с помощью векторной величины напряженности электрического поля E, либо с помощью скалярной величины φ. Связь между напряженностью поля и его потенциалом Сила связана с напряженностью
|
||||||||||||||||
|
Т. о. По известным значениям потенциала можно найти значение напряженности поля. Можно решить и обратную задачу, по заданным значениям напряженности в каждой точке найти разность потенциала между двумя произвольными точками поля.
Это
следует из формул для работы
|
Воображаемая
поверхность все точки которой имеют
одинаковый потенциал, называются
эквипотенциальной поверхностью. Ее
уравнение имеет вид
|
Отсюда заключаем, что вектор напряженности в каждой точке направлен по нормали к эквипотенциальной поверхности, проходящей через данную точку, а линии напряженности в каждой точке ортогональны эквипотенциальной поверхностям. Эквипотенциальную поверхность можно провести через любую точку поля и следовательно таких поверхностей можно построить бесконечное множество. , Условились проводить поверхности таким образом чтобы разность потенциалов для двух соседних поверхностей была всюду одной и той же. |
||||||||||||||||
|
Тогда по густоте эквипотенциальных поверхностей можно судить о величине напряженности поля. Для однородного поля эквипотенциальные поверхности представляют собой систему одинаково отстоящих друг от друга плоскостей перпендикулярных к направлению поля. |
7. Проводники в электростатическом поле. Напряженность поля внутри и вне проводника. Электроемкость проводника (рассмотреть проводник шарообразной формы) Носители заряда в проводнике способны перемещаться под действием сколь угодно малой силы. Поэтому для равновесия зарядов на проводнике необходимо выполнение следующих условий:
|
Следовательно в случае равновесия зарядов поверхность проводника будет эквипотенциальной. Если проводящему телу сообщить заряд q, то он распределиться так, чтобы соблюдались условия равновесия. Пусть имеет произвольную замкнутую поверхность полностью заключенную внутри тела. При равновесии зарядов поле в каждой точке отсутствует, поэтому поток электрического смещения равен нулю По теореме Гаусса сумма зарядов внутри поверхности тоже будет равна нулю. Следовательно при равновесии зарядов ни в каком месте проводника не может быть избытка зарядов, они распределяются равномерно по поверхности с некоторой плотностью σ.
|
||||||||||||||||
|
Избыточный
заряд распределяется на полом проводнике
также как и на сплошном – на наружной
поверхности. При внесении незаряженного
проводника в электрическое поле
носители заряда приходят в движение:
положительные в направлении вектора
|
Т.
о. нейтральный проводник, внесенный
в электрическое поле, разрывает часть
линий напряженности – они заканчиваются
на отрицательных индуцированных
зарядах и вновь начинаются на
положительных. Индуцированные заряды
распределяются во внешней поверхности
проводника. Если внутри проводника
имеется полость, то при равновесном
распределении зарядов поле внутри
проводника становится равным нулю
|
Внешнее поле компенсируется внутри экрана возникающими на его поверхности индуцированными зарядами. Такой экран может быть и не сплошным, а сделанным из густой сетки.
Электороемкость.
Пусть имеем уединенный проводник,
тогда его потенциал пропорционален
находящемуся на нем заряду. Действительно
увеличение увеличение в несколько
раз заряда приводит к увеличению в то
же число раз напряженности поля в
каждой точке окружающего проводник
пространства. Соответственно в такое
же число раз возрастает и работа
переноса единичного заряда из
бесконечности на поверхность проводника,
т.е. потенциал проводника. Т.о. для
уединенного проводника
|
||||||||||||||||
|
Коэффициент
пропорциональности С называется
электроемкостью проводника (или
емкостью)
Вычислим емкость уединенного шара. Сначала вычислим потенциал уединенного шара радиусом R. Между разностью потенциалов и напряженностью поля существует связь, |
поэтому
потенциал можно найти проинтегрировав
выражение для напряженности поля вне
сферы
|
8. Конденсаторы. Емкость плоского конденсатора. Последовательно и параллельное соединение конденсаторов. Энергия заряженного конденсатора. Плотность энергии электрического поля. Уединенные проводники обладают небольшой емкостью. Даже шар размером с Землю обладает емкостью только 700 мкФ. Однако на практике бывает потребность в устройствах, которые при небольшом относительно окружающих тел потенциале накапливали бы на себе (конденсировали) большие по величине заряды. Такие устройства называются конденсаторами и в их основу положен тот факт, что электроемкость проводников возрастает при приближении к ним других тел
|
||||||||||||||||
|
. Это вызвано тем, что под действием поля, создаваемого заряженным проводником, на поднесенном к нему теле возникают индуцированные заряды. Заряды противоположные по знаку заряду проводника q располагаются ближе к проводнику и оказывают влияние на проводник. А именно его потенциал уменьшается, а следовательно емкость возрастает. Конденсаторы делают в виде двух проводников, помещенных близко друг к другу, образующие конденсатор проводники называются его обкладками. Чтобы внешние тела не оказывали влияние на емкость конденсатора, их делают такими (по форме и расположению друг относительно друга), чтобы поле, создаваемое зарядами было сосредоточено внутри конденсатора. |
Это могут быть две пластинки, две концентрические сферы, два коаксиальных цилиндра. Следовательно, сущ. плоские, сферические и цилиндрические конденсаторы. Так как поле сосредоточено внутри конденсатора, линии напряженности начинаются на одной обкладке и заканчиваются на другой. И след. Сторонние заряды, возникающие на обкладках, имеют одинаковую величину и противоположны по знаку.
Основной
характеристикой конденсатора является
его емкость, под которой понимают
величину, пропорциональную заряду и
обратно пропорциональную разности
потенциалов между обкладками
|
Разность
потенциалов называют напряжением
между соответствующими точками и
обозначают буквой U (напряжение между
обкладками). Тогда можно переписать
формулу
|
||||||||||||||||
|
Например емкость
плоского конденсатора вычисляется
так. Если площадь обкладок равна S, а
заряд на ней q, то напряженность поля
между обкладками (поле 2 –х разноимееных
плоскостей)
Т.к. разность
потенциалов равна
Емкость сферического
конденсатора ,
|
Энергия электрического поля.
Заряд q, находящийся
на некотором проводнике можно
рассматривать как систему точечных
зарядов
|
Тогда энергия заряженного проводника
Пусть теперь
потенциал обкладки с зарядом +q равен
|
||||||||||||||||
|
Энергию заряженного конденсатора можно выразить через величины, характеризующие поле в зазоре
|
Если поле
однородно( например, поле плоского
конденсатора), заключенная в нем
энергия распределена в пространстве
равномерно, с постоянной плотностью
равной энергии деленной на объем
Зная плотность энергии можно вычислить энергию поля
|
Параллельное соединение конденсаторов. Параллельное соединение : соединены все положительные и отрицательно заряженные пластины между собой. Последовательное соединение: отрицательно заряженная пластина одного конденсатора соединена с положительно заряженной пластиной другого конденсатора рис. Ландсберг стр. 95
В случае
параллельного все конденсаторы
заряжаются до одного и того же напряжения
U, но заряды на них могут быть различными.
Если электроемкости равны С1, С2, Сn,
то заряды q1=C1U, q2=C2U и т.д. Q=q1+q2+…=(C1+C2+…)U
и след.
|
||||||||||||||||
|
В случае
последовательного соединения на вех
конденсаторах одинаковый заряд, но
разные напряжения U1=q/C1, U2=q/C2…Суммарное
напряжение между крайними (свободными)
пластинами U=U1+U2+…+Un= Т. О. электроемкость группы последовательно соединенных конденсаторов вседлв меньше чем параллельно соединенных.
|
9. Электрический дипольный момент электричекски нейтральной системы зарядов. Полярные и неполярные диэлектрики, их поляризация в электр. поле. Вектор поляризации. Диполем называется система двух разноименных зарядов одинаковых по величине +q и –q, расстояние l между которыми значительно меньше расстояния до тех точек системы, в которых определяется поле системы. Прямая, проходящая через оба заряда, называется осью диполя.
|
Вычислим потенциал поля диполя. Поле диполя обладает осевой симметрией. Поэтому поле в любой точке плоскости, проходящей через ось диполя будет одним и тем же и Е будет лежать в этой плоскости. Положение точки поля будем характеризовать радиус-вектором r и углом θ в полярных координатах. Введем вектор l от отрицательного заряда к положительному. Положение зарядов от центра диполя будем определять вектором а l=2a. Расстояние от точки до зарядов обозначим векторами r+ ,r-.
|
||||||||||||||||
|
Потенциал в точке
, p =ql – характеристика диполя – электрический момент Вектор р направлен по оси диполя от отрицательного заряда к положительному. |
Из формулы след., что поле диполя определяется его электрическим моментом р. Потенциал диполя убывает быстрее с расстоянием как 1/r2. Напряженность поля диполя
Положив θ=0, получим напряженность поля на оси диполя
Положив θ=π/.2, получим напряженность поля на оси диполя
|
Характерным для
напряженности поля является то
обстоятельство, что она убывает с
расстоянием от диполя как
Полярные и неполярные диэлектрики. Диэлектриками (изолятора ми) называются вещества, не способные проводить электрический ток. Все вещества могут проводить ток, однако вещества, проводящие ток в 1015 -1020 раз хуже, чем проводники, наз. диэлектриками.
|
||||||||||||||||
|
Всякая молекула
представляет собой систему зарядов,
причем суммарный заряд молекулы равен
нулю, молекула нейтральна. Поле,
создаваемое такой системой, определяется
величиной и ориентацией дипольного
электрического момента Поведение
молекулы во внешнем электрическом
поле определяется также ее дипольным
моментом
|
Т. о. молекула как в отношении создаваемого ей поля, так и в отношении испытываемых ее во внешнем поле сил эквивалентна диполю. Положительный заряд этого диполя равен суммарному заряду ядер и помещается в центр тяжести положительных зарядов, отрицательный заряд равен суммарному заряду электронов и помещается в центр тяжести отрицательных зарядов.
У симметричных
молекул (
|
Такие молекулы
не обладают собственным дипольным
моментом и называются неполярными. У
несимметричных молекул ( Под действием внешнего поля заряды в неполярной молекуле смещаются друг относительно друга: положительные по направлению поля, отрицательные против поля. В результате молекула приобретает дипольный момент.
|
||||||||||||||||
|
Если ввести
величину β – поляризуемость молекулы
и учесть, что направления ри
Е можно
записать
Размерность
Поляризация диэлектриков. В отсутствие внешнего поля дипольные моменты диэлектрика либо равны нулю (неполярные молекулы), либо распределены по направлениям в пространстве хаотическим образом (полярные молекулы). В обоих случаях суммарный дипольный момент равен нулю.
|
Под действием
внешнего поля диэлектрик поляризуется,
т.е результирующий дипольный момент
диэлектрика становится отличным от
нуля. В качестве величины, характеризующей
степень поляризации диэлектрика берут
дипольный момент единицы объема. Если
поле или диэлектрик (или они оба)
неоднородны, степень поляризации в
разных точках различен. Чтобы
охарактеризовать поляризацию в данной
точке, нужно выделить заключающий в
себе эту точку физически малый объем
|
Векторная величина
У изотропных
диэлектриков любого типа поляризованность
связана с напряженностью поля в той
же точке простым соотношением
|
||||||||||||||||
|
В случае полярных диэлектриков, ориентирующему действию внешнего поля противостоит тепловое движение молекул, которое стремится разбросать их дипольные моменты по всем направлениям. В результате устанавливается некоторая преимущественная ориентация дипольных моментов молекул в направлении поля. Поляризованность пропорциональна напряженности поля, т.е. соответствует формуле (выше). Диэлектрическая восприимчивость таких диэлектриков обратно пропорциональна абсолютной температуре. |
10. Электрическое поле в диэлектрике. Диэлектрическая проницаемость. Свойства полярных диэлектриков: пиро-, пьезо, сегнетоэлектричество. Заряды, входящие в состав молекулы диэлектрика назыв. связанными. Под действием поля связанные заряды могут только немного смещаться от своих положений равновесия и не могут покинуть пределы молекулы, в которую они входят. ами. Заряды, которые находятся в диэлектрике, но не входят в состав молекул или заряды за пределами диэлектрика назыв. сторонними.
|
Поле в диэлектрике является суперпозицией полей созданных сторонними зарядами и полей, созданных связанными зарядами. Результирующее поле назыв. Микроскопическим (или истинным):
Т.
к. микроскопическое поле сильно
изменяется в пределах молекулярных
расстояний, используют усредненные
по физически бесконечно малому объему
значение этих величин.
|
||||||||||||||||
|
Поляризованность
Р –
макроскопическая величина, поэтому
при ее вычислении под полем надо
подразумевать векторную сумму полей
сторонних зарядов и связанных. В
вакууме связанных зарядов нет и поле
равно полю сторонних зарядов. Можно
полу почить связь между плотностью
связанных зарядов и дивергенцией
поляризованности
|
В частности они
служат источниками электрического
поля, поэтому если плотность связанных
зарядов не равна нулю, дивергенцию
напряженности поля надо писать в виде:
).
|
В случае, когда
внутри диэлектрика нет сторонних
зарядов,
Перепишем формулу для дивергенции электрического поля в виде
|
||||||||||||||||
|
Т.о.
|
Сегнетоэлектрики. Сущ. Группа веществ, которые могут обладать спонтанной (самопроизвольной) поляризуемостью в отсутствие вешнего поля.Это явление было первоначально открыт для сегнетовой соли, поэтому вещества с такими свойствами назыв. сегнетоэлектриками. Особенности сегнетоэлектриков: 1 .у обычных диэлектриков ε несколько единиц и в исключительных случаях, как у воды ε=81 несколько десятков единиц, у сегнетоэлектриков ε бывает порядка нескольких тысяч. 2.Зависимость Р от Е не является линейной, и след. диэлектрическая проницаемость зависит от напряженности поля.
|
3.При изменении поля значение поляризованности Р зависит не только от величины поля в данный момент, но и от величины поля в предшествующие моменты, те.е. зависит от предистории диэлектрика. Это явление называется гистерезисом. (Петля гистерезиса, Сегнетоэлектриками могут быть только кристаллические вещества, у которых отсутствует центр симметрии. Взаимодействие частиц в кристалле приводит к тому, что их дипольные моменты спонтанно устанавливаются параллельно друг другу. Для каждого сегнетоэлектрика имеется характерная температура при которой вещество утрачивает необычные свойства. Эта температура назыв. точкой Кюри. Напр., сегнетовая соль имеет точку Кюри -15 С и +22С. |
||||||||||||||||
|
Пироэлектрики – кристаллические диэлектрики, на поверхности которых при изменении температуры возникают электрические заряды. Появление электрических зарядов связано с изменением спонтанной поляризации. Такими свойствами обладают кристаллы турмалина. Пьезоэлектрики – вещества, в которых при определенных упругих деформациях (напряженностях) возникает электрическая поляризация даже в отсутствие электрического внешнего поля. (прямой пьезоэффект), и наоборот под воздействием электрического поля возникает механические деформации (обратный пьезоэффект).
|
Наблюдается только в кристаллах, не имеющих центра симметрии. Используется в технике для преобразования механических колебаний в электрические и наоборот. Это основные материалы акустоэлектроники. Пьезозажигалка в быту. |
11. Постоянный электрический ток. Сила и плотность тока. Электродвижущая сила. Сопротивление проводников. Последовательное и параллельное соединение проводников. Закон Ома для однородного и неоднородного участков цепи. Всякое упорядоченное движение заряженных частиц называется электрическим током. За направление тока условно принимают направление движения положительных зарядов. Электрический ток, проходящий через данную поверхность, характеризуется силой тока I.
|
||||||||||||||||
|
Сила тока есть скалярная величина, численно равная заряду dq, который переноситься через площадку S в единицу времени, т.е.
Если за любые равные промежутки времени через любое сечение проводника проходят одинаковые количества электричества и направление движения зарядов не изменяется, то такой ток называется постоянным и тогда I=q/t. В системе СИ единица тока является основной и носит название - Ампер.
|
Электрический
ток может быть распределен по
поверхности, через которую он течет,
неравномерно.dI
Для характеристики направления
электрического тока в различных точках
рассматриваемой поверхности и
распределения силы тока по этой
поверхности вводится вектор
плотности
тока
|
Если ток постоянный, то выражение (17.2) можно переписать в виде: т.е.
плотность
тока
Если в проводнике создать электрическое поле и не принять мер для его поддержания, то, как было уже установлено, перемещение носителей заряда приведет очень быстро к тому, что поле внутри проводника исчезнет и, следовательно, ток прекратиться |
||||||||||||||||
|
.Для
того чтобы поддерживать ток достаточно
долго, нужно от конца проводника с
меньшим потенциалом (носители тока
предполагаются положительными)
непрерывно отводить приносимые сюда
током заряды, а к концу с большим
потенциалом непрерывно их подводить.
Т.е. необходимо осуществить круговорот
зарядов, при котором они двигались бы
по замкнутому пути (17.1). Циркуляция
вектора напряженности электростатического
поля равна нулю. Поэтому в замкнутой
цепи наряду с участками, на которых
положительные заряды движутся в
сторону убывания потенциала, должны
иметься участки, на которых перенос
положительных зарядов происходит в
направлении возрастания
|
Перемещение, зарядов на этих участках возможно лишь с помощью сил не электростатического происхождения, называемых сторонними силами. Таким образом, для поддержания тока необходимы сторонние силы, действующие либо на всем протяжении цепи, либо на отдельных ее участках. Они могут быть обусловлены химическими процессами, диффузией носителей заряда в неоднородной среде или через границу двух разнородных, веществ, электрическими (но не электростатическими) полями, порожденными меняющимися во времени магнитными полями и т.д.
|
Сторонние силы можно охарактеризовать работой, которую они совершают над перемещающимися по цепи зарядами. Эта работа складываеться из работы, совершаемой против электрического поля внутри источника тока (Аист и работы, совершаемой против сил сопративления среды (А’), т.е. Аст=Аист+А’
|
||||||||||||||||
|
Величина, равная отношению работы, которую совершают сторонние силы при перемещении точечного положительного заряда вдоль всей цепи, включая и источник тока, к заряду , называется электродвижущей силой источника тока:
Работа против сил электрического поля, по определению равна
Если
полюсы источника разомкнуты, то
т.е. эдс источника тока при разомкнутой внешней цепи равна разности потенциалов, которая создается на его полюсах.
|
Таким
образом, размерность эдс совпадает с
размерностью потенциала. Поэтому
Fст=E*q Векторную величину Е* называют напряженностью поля сторонних сил. Работу сторонних сил над зарядом q на всём протяжении замкнутой цепи можно выразить следующим образом:
Разделив эту работу на q , получим эдс, действующую в цепи:
|
Таким образом, эдс, действующая в замкнутой цепи, может быть определена как циркуляция вектора напряженности поля сторонних сил. Для участка цепи электродвижущая сила, действующая на некотором участке 1 -2 , очевидно равна
Кроме сторонних сил на заряд действуют силы электростатического поля
Следовательно, результирующая сила, действующая в каждой точке цепи на заряд q, равна
|
||||||||||||||||
|
Работа, совершаемая этой силой над зарядом q на участке цепи 1-2, дается выражением
Для замкнутой цепи работа электростатических сил равна нулю, так что
Величина,
численно равная работе, совершаемой
электростатическими и сторонними
силами при перемещении единичного
положительного заряда, называется
падением напряжения или просто
напряжением U
на данном участке цепи. Из
уравнения
|
При отсутствии сторонних сил напряжение U совпадает с разностью потенциалов
Закон Ома для однородного участка цепи Однородным называется участок цепи, в котором не действуют сторонние силы. Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения U на проводнике:
|
Величина R называется электрическим сопротивлением проводника. Единицей сопротивления служит Ом, равный сопротивлению такого проводника, в котором при напряжении 1В течет ток в 1 А. Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника .
|
||||||||||||||||
|
Закон Ома для неоднородного участка цепи Д
Умножим
скалярно обе части на вектор
|
Так
как скалярное произведение совпадающих
по направлению векторов
С И ( |
Подставляя (17.10), (17.9) и (17.8) в (17.7), окончательно получим
Последнее уравнение выражает собой закон Ома в интегральной форме для участка цепи, содержащего эдс и формулируется следующим образом: падение напряжения на участке цепи равно сумме падений электрического потенциала на этом участке и эдс всех источников электрической21 энергии, включённых на участке. |
||||||||||||||||
|
П
|
На
практике электрические цепи являются
совокупностью различных проводников,
определенным образом соединенных
между собой. При последовательном
соединении напряжение на каждом из
проводников пропорционально его
сопротивлению. Полное напряжение
|
При параллельном соединении силы токов в отдельных проводниках обратно пропорциаональны их сопротивлениям.
|
||||||||||||||||
|
12. Закон Ома в дифференциальной форме. Удельное сопротивление проводников, его зависимость от температуры. Явление сверхпроводимости. Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения U на проводнике:
Величина R называется электрическим сопротивлением проводника. Единицей сопротивления служит Ом, равный сопротивлению такого проводника, в котором при напряжении 1В течет ток в 1 А. Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан
|
. Для однородного цилиндрического проводника .
где
Величина обратная сопротивлению называется проводимостью
где
|
Закон
Ома можно записать в дифференциальной
форме. Выделим в проводнике элементарный
цилиндрический объем dV
с образующими, dl
параллельными вектору плотности тока
|
||||||||||||||||
|
Носители
заряда в каждой точке движутся в
направлении вектора
Явление сверхпроводимости. Согласно классической электронной теории, удельное сопротивление металлов должно монотонно уменьшаться при охлаждении, оставаясь конечным при всех температурах. Такая зависимость действительно наблюдается на опыте при сравнительно высоких температурах
|
. При более низких температурах порядка нескольких кельвинов удельное сопротивление многих металлов перестает зависеть от температуры и достигает некоторого предельного значения. Однако наибольший интерес представляет удивительное явление сверхпроводимости, открытое датским физиком Х. Каммерлинг-Оннесом в 1911 году. При некоторой определенной температуре Tкр, различной для разных веществ, удельное сопротивление скачком уменьшается до нуля (рис. 1.12.4). Критическая температура у ртути равна 4,1 К, у аллюминия 1,2 К, у олова 3,7 К. Сверхпроводимость наблюдается не только у элементов, но и у многих химических соединений и сплавов.
|
Например, соединение ниобия с оловом (Ni3Sn) имеет критическую температуру 18 К. Некоторые вещества, переходящие при низких температурах в сверхпроводящее состояние, не являются проводниками при обычных температурах. В то же время такие «хорошие» проводники, как медь и серебро, не становятся сверхпроводниками при низких температурах.
Зависимость удельного сопротивления ρ от абсолютной температуры T при низких температурах: a – нормальный металл; b – сверхпроводник |
||||||||||||||||
|
.Вещества в сверхпроводящем состоянии обладают исключительными свойствами. Практически наиболее важным их них является способность длительное время (многие годы) поддерживать без затухания электрический ток, возбужденный в сверхпроводящей цепи. Классическая электронная теория не способна объяснить явление сверхпроводимости. Объяснение механизма этого явления было дано только через 60 лет после его открытия на основе квантово-механических представлений. Научный интерес к сверхпроводимости возрастал по мере открытия новых материалов с более высокими критическими температурами.
|
Значительный шаг в этом направлении произошел в 1986 году, когда было обнаружено, что у одного сложного керамического соединения Tкр = 35 K. Уже в следующем 1987 году физики сумели создать новую керамику с критической температурой 98 К, превышающей температуру жидкого азота (77 К).Явление перехода веществ в сверхпроводящее состояние при температурах, превышающих температуру кипения жидкого азота, было названо высокотемпературной сверхпроводимостью. В 1988 году было создано керамическое соединение на основе элементов Tl–Ca–Ba–Cu–O с критической температурой 125 К.
|
В настоящее время ведутся интенсивные работы по поиску новых веществ с еще более высокими значениями Tкр. Ученые надеятся получить вещество в сверхпроводящем состоянии при комнатной температуре. Если это произойдет, это будет настоящей революцией в науке, технике и вообще в жизни людей. Следует отметить, что до настоящего времени механизм высокотемпературной сверхпроводимости керамических материалов до конца не выяснен.
|
||||||||||||||||
|
13. Закон Джоуля-Ленца в дифференциальной и интегральной форме. Если
в проводнике течет постоянный ток и
проводник остается неподвижным, то
работа сторонних сил расходуется на
его нагревание. Опыт показывает, что
в любом проводнике происходит выделение
теплоты, равное работе, совершаемой
электрическими силами по переносу
заряда вдоль проводника. Если на концах
участка проводника имеется разность
потенциалов
По определению I= q/t. откуда q= I t.
|
Следовательно
Так как работа идет па нагревание проводника, то выделяющаяся в проводнике теплота Q равна работе электростатических сил
Соотношение (17.13) выражает закон Джоуля-Ленца в интегральной форме. Введем
плотность тепловой мощности
где
S
- поперечное сечение проводника,
|
Используя
(1.13) и соотношение
с
учетом закона Ома в дифференциальной
форме
Формула (17.14) выражает закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля.
|
||||||||||||||||
|
14. Магнитное поле, создаваемое постоянными электрическими токами. Взаимодействие параллельных бесконечных проводников с током, единица Ампер в СИ. Опыт показывает, что электрические токи взаимодействуют между собой. Например, два тонких прямолинейных параллельных проводника, по которым текут токи (прямые токи), притягивают друг друга, если токи в них имеют одинаковое направление, и отталкивают, если токи противоположны.
|
Сила
взаимодействия, приходящаяся на
единицу длины каждого из параллельных
проводников, пропорциональна величинам
токов в них
Коэффициент пропорциональности 2k. Закон взаимодействия токов был установлен в 1820 г. Ампером. На основании этого соотношения устанавливается единица силы тока в СИ и в абсолютной электромагнитной системе единиц (СГСМ- системе).
|
Единица
силы тока в СИ — ампер — определяется
как сила неизменяющегося тока, который,
проходя по двум параллельным
прямолинейным проводникам бесконечной
длины и ничтожно малого кругового
сечения, расположенным на расстоянии
1 м один от другого в вакууме, вызвал
бы между этими проводниками силу,
равную
|
||||||||||||||||
|
В
системе единиц СИ это соотношение
записывается следующим образом:
где
Чтобы
найти числовое значение
тем,
что согласно определению ампера при
|
Магнитное поле Взаимодействие токов осуществляется через поле, называемое магнитным. Это название происходит от того, что, как обнаружил в 1820 г. Эрстед, поле, возбуждаемое током, оказывает ориентирующее действие на магнитную стрелку. В опыте Эрстеда проволока, по которой тек ток, была натянута над магнитной стрелкой, вращающейся на игле. При включении тока стрелка устанавливалась перпендикулярно к проволоке. Изменение направления тока заставляло стрелку повернуться в противоположную сторону. Из опыта Эрстеда следует, что магнитное поле имеет направленный характер и должно характеризоваться векторной величиной.. |
Эту величину принято обозначать буквой В. Логично было бы по аналогии с напряженностью электрического поля Е назвать В напряженностью магнитного поля. Однако по историческим причинам основную силовую характеристику магнитного поля назвали магнитной индукцией. Название же «напряженность магнитного поля» оказалось присвоенным вспомогательной величине Н, аналогичной вспомогательной характеристике D электрического поля. Магнитное поле, в отличие от электрического, не оказывает действия на покоящийся заряд Сила возникает лишь тогда, когда заряд движется. |
||||||||||||||||
|
Проводник с током представляет собой электрически нейтральную систему зарядов, в которой заряды одного знака движутся в одну сторону, а заряды другого знака движутся в противоположную сторону (либо покоятся). Отсюда следует, что магнитное поле порождается движущимися зарядами. Итак, движущиеся заряды (токи) изменяют свойства окружающего их пространства — создают в нем магнитное поле. Это поле проявляется в том, что на движущиеся в нем заряды (токи) действуют силы.
|
Опыт
дает, что для магнитного поля, как и
для электрического, справедлив принцип
суперпозиции: поле В, порождаемое
несколькими движущимися зарядами
(токами), равно векторной сумме полей
порождаемых каждым зарядом (током) в
отдельности:
Пространство изотропно, поэтому, если заряд неподвижен, все направления оказываются равноправными. Этим обусловлен тот факт, что создаваемое точечным зарядом электростатическое поле является сферически-симметричным. В случае движения заряда со скоростью v в пространстве появляется выделенное направление (направление вектора v). |
Поэтому можно ожидать, что магнитное поле, создаваемое движущимся зарядом, обладает осевой симметрией.
Рассмотрим
магнитное поле, создаваемое в некоторой
точке Р точечным зарядом q, движущимся
с постоянной скоростью v. Возмущения
поля передаются от точки к точке с
конечной скоростью с. Поэтому индукция
В в точке Р в момент времени t определяется
не положением заряда в тот же момент
t,
а положением заряда в некоторый более
ранний момент времени
|
||||||||||||||||
|
Здесь
Р означает совокупность координат
точки Р, определяемых в некоторой
неподвижной системе отсчета, r(t—т) —
радиус-вектор, проведенный в точку Р
из той точки, в которой находился заряд
в момент времени
Вид функции B может быть установлен только экспериментально. .
|
Опыт
дает, ято в случае, когда v<<c,
магнитная индукция поля движущегося
заряда определяется формулой
Эта формула может быть получена только экспериментально. Из соотношения вытекает, что вектор В в каждой точке Р направлен перпендикулярно к плоскости, проходящей через направление вектора v и точку Р, причем так, что вращение в направлении В образует с направлением v правовинтовую систему |
15. Вектор магнитной индукции, определение направления и величины. Силовые линии магнитного поля. Поток вектора магнитной индукции через замкнутую поверхность. Принцип суперпозиции.
МАГНИТНЫЕ СИЛЫ- это силы, с которыми проводники с током действуют друг на друга.
|
||||||||||||||||
|
.МАГНИТНАЯ ИНДУКЦИЯ - это силовая характеристика магнитного поля.
Вектор магнитной индукции направлен всегда так, как сориентирована свободно вращающаяся магнитная стрелка в магнитном поле. Единица измерения магнитной индукции в системе СИ: ЛИНИИ МАГНИТНОЙ ИНДУКЦИИ -
|
Однородное магнитное поле - это магнитное поле, у которого в любой его точке вектор магнитной индукции неизменен по величине и направлению; наблюдается между пластинами плоского конденсатора, внутри соленоида (если его диаметр много меньше его длины) или внутри полосового магнита. М
|
Магнитное поле соленоида:
Магнитное поле полосового магнита: - аналогично магнитному полю соленоида. СВОЙСТВА ЛИНИЙ МАГНИТНОЙ ИНДУКЦИИ
|
||||||||||||||||
|
НАПРАВЛЕНИЕ ЛИНИЙ МАГНИТНОЙ ИНДУКЦИИ - определяется по правилу буравчика или по правилу правой руки. Правило буравчика ( в основном для прямого проводника с током): Если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитного поля тока.
|
Правило правой руки ( в основном для определения направления магнитных линий внутри соленоида): Если обхватить соленоид ладонью правой руки так, чтобы четыре пальца были направлены вдоль тока в витках, то отставленный большой палец покажет направление линий магнитного поля внутри соленоида. Отсутствие в природе магнитных зарядов приводит к тому, что линии вектора В не имеют ни начала, ни конца. Поэтому поток вектора В через замкнутую поверхность должен быть равен нулю. |
Таким
образом, для любого магнитного поля
и произвольной замкнутой поверхности
S имеет место условие
Условие, к которому мы пришли, должно выполняться для любого произвольно выбранного объема V. Это возможно лишь в том случае, если подынтегральная функция в каждой точке поля равна нулю. |
||||||||||||||||
|
Таким образом, магнитное поле обладает тем свойством, что его
дивергенция всюду равна нулю:
Опыт
дает, что для магнитного поля, как и
для электрического, справедлив принцип
суперпозиции: поле В, порождаемое
несколькими движущимися зарядами
(токами), равно векторной сумме полей
порождаемых каждым зарядом (током) в
отдельности:
|
16. Закон Био — Савара- Лапласса. Магнитное поле, создаваемое круговым током, бесконечным прямолинейным проводником с током.
Выясним
характер магнитного поля, создаваемого
произвольным тонким проводом, по
которому течет ток. Рассмотрим малый
элемент провода длины dl. В этом элементе
содержится nS dl носителей тока (n
— число носителей в единице объема,
S
— площадь попе- речного сечения провода
в том месте, где взят элемент dl). В точке
положение которой относительно
элемента dl определяется радиусом-вектором
г (отдельный носитель тока е создает
поле с индукцией
Здесь v — скорость хаотического движения, а u — скорость упорядоченного движения носителя. |
Значение
магнитной индукции, усредненное по
носителям тока, заключенным в элементе
dl, равно
(<v>=0). Умножив это выражение на число носителей в элементе провода (равное nS dl), получим вклад в поле, вносимый элементом dl: (мы внесли скалярные множители n и е под
знак векторного произведения).
|
||||||||||||||||
|
Введем
вектор
Произведя
такую замену в формуле для dB,
получим
Учли,
что произведение Sj дает силу тока I
в проводе, придем к окончательному
выражению, определяющему магнитную
индукцию поля, создаваемого элементом
тока длины dl:
|
Мы вывели формулу. В действительности последняя формула была установлена экспериментально. Био и Савар провели в 1820 г. исследование магнитных полей, текущих по тонким проводам различной формы. Лаплас проанализировал экспериментальные данные, полученные Био и Саваром, и нашел, что магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельным, элементарными участками токов. Для
магнитной индукции поля, создаваемого
элементом тока длины dl,
Лаплас получил формулу
|
.Из
рис. 42.1видно, что вектор dB направлен
перпендикулярно к плоскости, проходящей
через dl
и точку, в которой вычисляется поле,
причем так, что вращение вокруг dl
в направлении dB
связано с dl
правилом правого винта. Модуль dB
определяется выражением
где α— угол между векторами dl и г. Применим формулу закона Б-С-Л для вычисления поля прямого тока, т. е. поля, создаваемого током, текущим по тонкому прямому проводу бесконечной длины (рис. 42.2 Сав 122). Все векторы dB в данной точке имеют одинаковое направление (в нашем случае за чертеж).
|
||||||||||||||||
|
Поэтому сложение векторов dB можно заменить сложением их модулей. Точка, для которой мы вычисляем магнитную индукцию, находится на расстоянии b от провода.
Из
рис. 42.2 видно, что
Угол α для всех элементов бесконечного прямого тока изменяется от 0 до π. |
Следовательно, магнитная индукция поля прямого тока определяется формулой
(рис. 42.3 Сав 122). 16. Магнитное поле кругового контура с током Рассмотрим поле, создаваемое током, текущим по тонкому проводу, имеющему форму окружности радиуса R (круговой ток). Определим магнитную индукцию в центре кругового тока (рис. 47.1 Сав. 138).
|
Каждый элемент тока создает в центре индукцию, направленную вдоль положительной нормали к контуру. Поэтому векторное сложение dВ сводится к сложению их модулей.
По
формуле
|
||||||||||||||||
|
Из
рис. 47.1 видно, что направление вектора
В совпадает с направлением положительной
нормали к контуру, т. е. с направлением
вектора pm.
Поэтому последнюю формулу можно
написать в векторном виде:
Теперь найдем В на оси кругового тока на расстоянии г от центра контура (рис. 47.2 Сав.138). Векторы dB перпендикулярны к плоскостям, проходящим через соответствующий элемент dl и точку, в которой мы ищем поле. Следовательно, они образуют симметричный конический веер (рис. 47.2, б, Cfd 138). Из соображений симметрии можно заключить, что результирующий вектор В направлен вдоль оси контура
|
.
Каждый из составляющих векторов dB
вносит в результирующие вектор вклад
Проинтегрировав
по всему контуру и заменив b на
|
Приняв
во внимание, что векторы В
и pm
имеют одинаковое направление, можно
написать последнюю формулу в векторном
виде:
Это
выражение не зависит от знака г.
Следовательно, в точках оси, симметричных
относительно центра тока, В имеет
одинаковую величину и направление.
При г=0 формула переходит, как и должно
быть |
||||||||||||||||
|
17. Теорема о циркуляции вектора магнитной индукции, ее применение для расчета магнитного поля в бесконечном соленоиде. Отсутствие
в природе магнитных зарядов приводит
к тому, что линии вектора В не имеют
ни начала, ни конца. Поэтому поток
вектора В
через замкнутую поверхность должен
быть равен нулю. Таким образом, для
любого магнитного поля и произвольной
замкнутой поверхности S имеет место
условие
|
Заменив
поверхностный интеграл объемным,
получим, что
Условие, к которому мы пришли, должно выполняться для любого произвольно выбранного объема V. Это возможно лишь в том случае, если подынтегральная функция в каждой точке поля равна нулю. Таким образом, магнитное поле обладает тем свойством, что его
дивергенция всюду равна нулю:
Найдем
циркуляции вектора В.
По определению циркуляция равна
интегралу
|
Проще всего вычислить этот интеграл в случае поля прямого тока. Пусть замкнутый контур лежит в плоскости, перпендикулярной к току (рис. ; ток перпендикулярен к плоскости чертежа и направлен за чертеж). В каждой точке контура вектор В направлен по касательной к окружности, проходящей через эту точку. Заменим в выражении для циркуляции В dl через В dlB (dlB — проекция элемента контура на направление вектора В).
|
||||||||||||||||
|
Из
рисунка видно, что dlB
равно b dα, где b
— расстояние от провода с током до
dl,
dα — угол, на который поворачивается
радиальная прямая при перемещении
вдоль контура на отрезок dl.
Таким образом, для В,
получим
Окончательно
будем иметь
При
обходе по контуру, охватывающему ток,
радиальная прямая все время поворачивается
в одном направлении, поэтому
|
Иначе
обстоит дело, если ток не охватывается
контуром (рис. 49.1 ,б). В этом случае при
обходе по контуру радиальная прямая
поворачивается сначала в одном
направлении (участок 1—2), а затем в
противоположном (участок 2—1), вследствие
чего
|
Если
направление обхода образует с
направлением тока правовинтовую
систему, величина
Соленоид представляет собой провод, навитый на круглый цилиндрический каркас. Линии В поля соленоида выглядят пример но так, как показано на рис. 50.1.
|
||||||||||||||||
|
Внутри
соленоида направление этих линий
образует с направлением тока в витках
правовинтовую систему. У реального
соленоида имеется составляющая тока
вдоль оси. Кроме того, линейная плотность
тока jлин
(равная отношению силы тока dI
к элементу длины соленоида dl)
изменяется периодически при перемещении
вдоль соленоида. Среднее значение
этой плотности равно
|
В соответствии со сказанным представим соленоид в виде бесконечного тонкостенного цилиндра (отсутствует осевая составляющая тока и, кроме того, линейная плотность тока jлин постоянна по всей длине), обтекаемого током постоянной линейной плотности jлин=nI. Разобьем цилиндр на одинаковые круговые токи—«витки». Из.рис. видно, что каждая пара витков, расположенных симметрично относительно некоторой плоскости, перпендикулярной к оси соленоида, создает в любой точке этой плоскости магнитную индукцию, параллельную оси. Следовательно, и результирующее поле в любой точке внутри и вне бесконечного соленоида может иметь лишь направление, параллельное оси. |
Из
рис. 50.1 вытекает, что направления поля
внутри и вне конечного соленоида
противоположны. При увеличении длины
соленоида направления полей не
изменяются и в пределе при
|
||||||||||||||||
|
Обойдя контур по часовой стрелке, получим для циркуляции вектора В значение (B2 –B1)α. Контур не охватывает токов, поэтому циркуляция должна быть равна нулю. Отсюда следует, что B1=B2. Располагая участок контура 2—3 на любом расстоянии от оси, мы каждый раз будем получать, что магнитная индукция В2 на этом расстоянии равна индукции B1 на оси соленоида. Таким образом, однородность поля внутри соленоида доказана. Теперь обратимся к контуру 1'—2'—3'—4'. Мы изобразили векторы B`1и В`2 штриховой линией, поскольку, поле вне бесконечного соленоида равно нулю. Контур 1'—2'—3'—4'не охватывает токов; поэтому циркуляция вектора В' по этому контуру, равная (B`1-В`2 )α, должна быть равна нулю.
|
Отсюда вытекает, что B`1= В`2 . Расстояния от оси соленоида до участков /' — 4' и 2' — 3' были взяты произвольно. Следовательно, значение В' на любом расстоянии от оси будет вне соленоида одно и то же. Таким образом, оказывается доказанной и однородность поля вне соленоида. Циркуляция по контуру, изображенному на рис. 50.4 (Сав. 150), равна α(В+В') (для обхода по часовой стрелке). Этот контур охватывает положительный ток величины jлин α.
Должно
выполняться равенство
|
Возьмем плоскость, перпендикулярную к оси соленоида (рис. 50.5 Сав 151). Вследствие замкнутости линий В магнитные потоки через внутреннюю часть S этой плоскости и через внешнюю часть S' должны быть одинаковыми. Поскольку поля однородны и перпендикулярны к плоскости, каждый из потоков равен произведению соответствующего значения магнитной индукции и площади, пронизываемой потоком. Таким образом, получается соотношение BS=B'S'. Левая часть этого равенства конечна, множитель S' в правой части бесконечно большой. Отсюда следует, что В'=0. Итак, мы доказали, что вне бесконечно длинного соленоида магнитная индукция равна нулю. Внутри соленоида поле однородно.
|
||||||||||||||||
|
Положив
В'=0, придем к формуле для магнитной
индукции внутри соленоида:
В
магнитную индукцию на оси соленоида
симметрично расположенные витки
вносят одинаковый вклад. Поэтому у
конца полубесконечного соленоида на
его оси магнитная индукция равна
половине значения :
|
Практически,
если длина соленоида значительно
больше, чем его диаметр, формула
|
18. Сила, действующая на проводник с током в магнитном поле- сила Ампера. Поведение рамки с током в магнитном поле. Если
провод, по которому течет ток, находится
в магнитном поле, на каждый из носителей
тока действует сила
|
||||||||||||||||
|
Найдем
величину силы dF, действующей на элемент
провода длины dl. Усредним выражение
Умножив полученное выражение на число носителей, найдем интересующую нас силу:
|
Приняв
во внимание, что ne<u>есть
плотность тока j
a S dl дает объем элемента провода dV,
можно написать
|
ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА РАМКУ С ТОКОМ Однородное магнитное поле ориентирует рамку (т.е. создается вращающий момент и рамка поворачивается в положение, когда вектор магнитной индукции перпендикулярен плоскости рамки).
Н
|
||||||||||||||||
|
Т
|
19. Движение заряженных частиц в магнитном поле. Сила Лоренца На заряд, движущийся в магнитном поле, действует сила, которую мы будем называть магнитной. Эта сила определяется зарядом q, скоростью его движения v и магнитной индукцией В в той точке, где находится заряд в рассматриваемый момент времени. Простейшее предположение заключается в том, что модуль силы F пропорционален каждой из трех величин q, v и В. Кроме того, можно ожидать, что F зависит от взаимной ориентации векторов v и В. Направление вектора F должно определяться направлениями векторов v и В. ы. |
Опытным
путем установлено, что сила F, действующая
на заряд, движущийся в магнитном поле,
определяется формулой
. |
||||||||||||||||
|
Модуль
магнитной силы равен
где α— угол между векторами v и В Из последней формулы вытекает, что заряд, движущийся вдоль линий магнитного поля, не испытывает действия магнитной сил Направлена магнитная сила перпендикулярно к плоскости, в которой лежат векторы v и В. Если заряд q положителен, направление силы совпадает с направлением вектора [vB]. В случае отрицательного q направления векторов F и [vB] противоположны (рис. 43.1 Сав. 124). Поскольку магнитная сила всегда направлена перпендикулярно к скорости заряженной частицы, она не совершает работы над частицей. |
Следовательно,
действуя на заряженную частицу
постоянным магнитным полем, изменить
ее энергию нельзя. Если имеются
одновременно электрическое и магнитное
поля, сила, действующая на заряженную
частицу, равна
|
20. Вещество в магнитном поле. Вектор наманниченности. Связь молекулярных токов с величиной вектора намагниченности. Магнитная проницаемость, восприимчивость. Если
несущие ток провода находятся в
какой-либо среде, магнитное поле
изменяется. Это объясняется тем, что
всякое вещество является магнетиком,
т. е. способно под действием магнитного
поля приобретать магнитный момент
(намагничиваться). Намагниченное
вещество создает магнитное поле В',
которое накладывается на обусловленное
токами поле Во.
Оба поля в сумме дают результирующее
поле
|
||||||||||||||||
|
Под В подразумевается усредненное (макроскопическое) поле. Для объяснения намагничения тел Ампер предположил, что в молекулах вещества циркулируют круговые токи (молекулярные токи). Каждый такой ток обладает магнитным моментом и создает в окружающем пространстве магнитное поле. В отсутствие внешнего поля молекулярные токи ориентированы беспорядочным образом, вследствие чего обусловленное ими результирующее поле равно нулю. В силу хаотической ориентации магнитных моментов отдельных молекул суммарный магнитный момент тела также равен нулю. |
.
Под действием поля магнитные моменты
молекул приобретают преимущественную
ориентацию в одном направлении,
вследствие чего магнетик намагничивается
— его суммарный магнитный момент
становится отличным от нуляМагнитные
поля отдельных молекулярных токов в
этом случае уже не компенсируют друг
друга и возникает поле В'. Намагничение
магнетика естественно характеризовать
магнитным моментом единицы объема.
Эту величину называют намагниченностью
(вектор намагниченности) и обозначают
буквой J.
Если магнетик намагничен неоднородно,
намагниченность в данной точке
определяется следующим выражением:
|
где
Суммирование
производится по всем молекулам,
заключенным в объеме
Можно
найти такую вспомогательную величину,
ротор которой определяется лишь
плотностью макроскопических токов.
Чтобы установить вид этой вспомогательной
величины, выразим плотность молекулярных
токов
|
||||||||||||||||
|
С
этой целью вычислим алгебраическую
сумму молекулярных токов, охватываемых
некоторым контуром Г
|
Из рис. видно, что элемент контура dl, образующий с направлением намагниченности J угол α, нанизывает на себя те молекулярные токи, центры которых попадают внутрь косого цилиндра с объемом Sмол cos α dl(Sмол — площадь, охватываемая отдельным молекулярным током). Если n — число молекул в единице объема, то суммарный ток, охватываемый элементом dl, равен IмолnSмол cos α dl. Произведение IмолSмол равно магнитному моменту рm отдельного молекулярного тока. Следовательно, выражение IмолnSмол представляет собой магнитный момент единицы объема, т. е. дает модуль вектора j, a IмолnSмол cos α проекцию вектора j на направление элемента dl. |
Таким
образом, суммарный молекулярный ток,
охватываемый элементом dl,
равен j
dl,
а сумма молекулярных токов, охватываемых
всем контуром равна
|
||||||||||||||||
|
Таким образом, плотность молекулярных токов определяется значением ротора намагниченности. В случае, когда [yJ]=0, молекулярные токи отдельных молекул ориентированы так, что их сумма в среднем равна нулю. Выражение
|
Если макроскопические токи текут по проводам, охватываемым контуром, то - теорема о циркуляции вектора Н: циркуляция вектора напряженности магнитного поля по некоторому контуру равна алгебраической сумме макроскопических токов, охватываемых этим контуром. Напряженность магнитного поля Н является аналогом электрического смещения D. Первоначально предполагалось, что в природе имеются подобные электрическим зарядам магнитные массы, и учение о магнетизме развивалось по аналогии с учением об электричестве. В те времена и были введены названия: «магнитная индукция» для В и «напряженность поля» для Н. |
Впоследствии выяснилось, что магнитных масс в природе не существует и что величина, названная магнитной индукцией, в действительности является аналогом не электрического смещения D, а напряженности электрического поля Е (соответственно Н — аналогом не Е, a D). Однако изменять уже установившуюся терминологию не стали, тем более, что вследствие различной природы электрического и магнитного полей (электростатическое поле потенциально, магнитное — соленоидально *)) величины В и D обнаруживают много сходства в своем поведении (например, линии В, как и линии D, не претерпевают разрыва на границе двух сред). В вакууме J=0, поэтому Н превращается в В . |
||||||||||||||||
|
Напряженность магнитного поля имеет размерность, равную размерности силы тока, деленной на размерность длины. В связи с этим единица напряженности магнитного поля в СИ носит название ампер на метр (А/м). Из этого определения следует, что в вакууме Н совпадает с В. В соответствии с этим единица Н в гауссовой системе, называемая эрстедом (Э), имеет ту же величину и размерность, что и единица магнитной индукции — гаусс (Гс). По существу эрстед и гаусс суть разные названия одной и той же единицы. Если этой единицей измеряют Н, ее называют эрстедом, если измеряют В, то — гауссом.
|
Намагниченность
принято связывать не с магнитной
индукцией, а с напряженностью поля.
Полагают, что в каждой точке магнетика
|
В отличие от диэлектрической восприимчивости κ которая может иметь лишь положительные значения (поляризованность Р в изотропном диэлектрике всегда направлена по полю Е), магнитная восприимчивость χ бывает как положительной, так и отрицательной. Поэтому магнитная проницаемость и. может быть как больше, так и меньше единицы. Таким
образом, напряженность магнитного
поля Н
есть вектор, имеющий то же направление,
что и вектор В, но в
|
||||||||||||||||
|
21. Пар-, ферро- диамагнетики. Постоянные магниты. Формула
|
В зависимости от знака и величины магнитной восприимчивости все магнетики подразделяются на три группы:
|
Таким образом, в изотропных веществах намагниченность J может как совпадать по направлению с Н (у пара- и ферромагнетиков), так и быть направленной в противоположную сторону (у диамагнетиков). Постоянный магнит — изделие различной формы из магнитотвёрдого материала с высокой остаточной магнитной индукцией, сохраняющее состояние намагниченности в течение длительного времени. Постоянные магниты применяются в качестве автономных (не потребляющих энергии) источников магнитного поля.
|
||||||||||||||||
|
Семейство петель магнитного гистерезиса электротехнической стали. Br — остаточная индукция, Hc — коэрцитивная сила, внешняя петля соответствует состоянию насыщения. Свойства магнита определяются характеристиками размагничивающего участка петли магнитного гистерезиса материала магнита: чем выше остаточная индукция Br и коэрцитивная сила Hc, тем выше намагниченность и стабильность магнита. Магнитный Гистерезис наблюдается в магнитных материалах, например в ферромагнетиках. Основной особенностью ферромагнетиков является наличие спонтанной (самопроизвольной) намагниченности.
|
Обычно ферромагнетик намагничен не однородно, а разбит на домены — области однородной спонтанной намагниченности, у которых величина намагниченности (магнитного момента единицы объема) одинакова, а направления различны .
|
На рис. 1 изображена зависимость магнитного момента М ферромагнитного образца от напряжённости Н внешнего магнитного поля (кривая намагничивания). В достаточно сильном магнитном поле образец намагничивается до насыщения (при дальнейшем увеличении поля значение М практически не изменяется, точка А). При этом образец состоит из одного домена с магнитным моментом насыщения Ms, направленным по полю. При уменьшении напряжённости внешнего магнитного поля Н магнитный момент образца М будет уменьшаться по кривой I преимущественно за счёт возникновения и роста доменов с магнитным моментом, направленным против поля. Рост доменов обусловлен движением доменных стенок. |
||||||||||||||||
|
Это движение затруднено из-за наличия в образце различных дефектов (примесей, неоднородностей и т.п.), которые закрепляют доменные стенки в некоторых положениях; требуются достаточно сильные магнитные поля для того, чтобы их сдвинуть. Поэтому при уменьшении поля Н до нуля у образца сохраняется т. н. остаточный магнитный момент Mr (точка В).Рис. 1. Петля магнитного гистерезиса для ферромагнетика: Н — напряжённость магнитного поля; М — магнитный момент образца; Нс — коэрцитивное поле; Mr — остаточный магнитный момент; Ms — магнитный момент насыщения. Пунктиром показана непредельная петля гистерезиса. Схематически приведена доменная структура образца для некоторых точек петли. |
Образец полностью размагничивается лишь в достаточно сильном поле противоположного направления, называемом коэрцитивным полем (коэрцитивной силой) Нс (точка С). При дальнейшем увеличении магнитного поля обратного направления образец вновь намагничивается вдоль поля до насыщения (точка D). Перемагничивание образца (из точки D в точку А) происходит по кривой II. Т. о., при циклическом изменении поля кривая, характеризующая изменение магнитного момента образца, образует петлю магнитного Гистерезис Если поле Н циклически изменять в таких пределах, что намагниченность насыщения не достигается, то получается непредельная петля магнитного Гистерезис (кривая III). |
Уменьшая амплитуду изменения поля Н до нуля, можно образец полностью размагнитить (прийти в точку О). Намагничивание образца из точки О происходит по кривой IV. Индукция постоянного магнита Bd не может превышать Br: равенство Bd = Br возможно лишь в том случае, если магнит представляет собой замкнутый магнитопровод, то есть не имеет воздушного промежутка, однако постоянные магниты, как правило, используются для создания магнитного поля в воздушном (или заполненном другой средой) зазоре, в этом случае Bd < Br, величина разности зависит от формы магнита и свойств среды. Для производства постоянных магнитов обычно используются следующие материалы: |
||||||||||||||||
|
Бариевые и стронциевые магнитотвердые ферриты Имеют состав Ba/SrO·6 Fe2O3 и характеризуются высокой устойчивостью к размагничиванию в сочетании с хорошей коррозионной стойкостью. Несмотря на низкие по сравнению с другими классами магнитные параметры и высокую хрупкость, благодаря низкой стоимости магнитотвердые ферриты наиболее широко применяются в промышленности. Магниты NdFeB (неодим-железо-бор) Редкоземельные магниты, изготавливаемые прессованием или литьем из интерметаллида Nd2Fe14B. Преимуществами этого класса магнитов являются высокие магнитные свойства (Br, Hc и (BH)max), а также невысокая стоимость. В связи со слабой коррозионной устойчивостью обычно покрываются медью, никелем или цинком. |
Редкоземельные магниты SmCo (Самарий-Кобальт) Изготавливаются методом порошковой металлургии из композиционного сплава SmCo5/Sm2Co17 и характеризуются высокими магнитными свойствами, отличной коррозионной устойчивостью и хорошей стабильностью параметров при температурах до 350 °C,что обеспечивает им преимущества на высоких температурах перед магнитами NdFeB Магниты ALNICO (российское название ЮНДК)Изготавливаются основе сплава Al-Ni-Co-Fe. К их преимуществам можно отнести высокую температурную стабильность в интервале температур до 550 °C, высокую временну́ю стабильность параметров в сочетании с большой величиной коэрцитивной силы, хорошую коррозионную устойчивость |
Полимерные постоянные магниты (магнитопласты) Изготавливаются из смеси магнитного порошка и связующей полимерной компоненты (например резины). Достоинством магнитопластов является возможность получения сложных форм изделий с высокой точностью размеров, а также высокая коррозионная устойчивость в сочетании с большой величиной удельного сопротивления и малым весом. Наиболее широко распространены ферритовые магниты. Для применений при обычных температурах самые сильные постоянные магниты делаются из сплавов, содержащих неодим. Они используются в таких областях, как магнитно-резонансная томография, сервоприводы жёстких дисков и создание высококачественных динамиков |
||||||||||||||||
|
. 22. Явление электромагнитной индукции. Правило Ленца. Закон Фарадея. В 1831 г. Фарадей обнаружил, что в замкнутом проводящем контуре при изменении потока магнитной индукции через поверхность, ограниченную этим контуром, возникает электрический ток. Это явление называют электромагнитной индукцией, а возникающий ток индукционным. Явление электромагнитной индукции свидетельствует о том, что при изменениях магнитного потока в контуре возникает электродвижущая сила индукции - εi. Величина εi не зависит от способа, которым осуществляется изменение магнитного потока Ф, и определяется лишь скоростью изменения Ф, т. е. значением dФ/dt. При изменении знака dФ/dt. направление εi также меняется. |
Ленц установил правило, позволяющее найти направление индукционного тока. Правило Ленца гласит, что индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей. Если, например, изменение Ф вызвано перемещением контура 2, то возникает индукционный ток такого направления, что сила взаимодействия с первым контуром противится движению контура. При приближении контура 2 к контуру 1 (см. рис. 60.1 Сав 181) возникает ток I2, магнитный момент которого направлен противоположно полю тока. Следовательно, на контур 2 будет действовать сила, отталкивающая его от контура При удалении контура 2 от контура 1 возникает ток I2 так что сила, действующая на контур 2, направлена к контуру 1. |
Пусть оба контура неподвижны и ток в контуре 2 индуцируется путем изменения тока I1 в контуре 1. В этом случае возникает ток I2 такого направления, что создаваемый им собственный магнитный поток стремится ослабить изменения внешнего потока, приведшие к появлению индукционного тока. При увеличении I1, т. е. возрастании внешнего магнитного потока, направленного вправо, возникает ток I2, создающий поток, направленный влево. При уменьшении I1 возникает ток I2, собственный магнитный поток которого направлен так же, как и внешний поток, и, следовательно, стремится поддержать внешний поток неизменным.
|
||||||||||||||||
|
Возьмем контур с подвижной перемычкой длины l (рис. 61.1, а, Сав 183). Поместим
его в однородное магнитное поле,
перпендикулярное к плоскости контура
и направленное за чертеж. Приведем
перемычку в движение со скоростью v.
С той же скоростью станут перемещаться
относительно поля и носители тока в
перемычке — электроны. В результате
на каждый электрон начнет действовать
направленная вдоль перемычки магнитная
сила.
Действие этой силы эквивалентно действию на электрон электрического поля напряженности E=[vB]. Это поле не электростатического происхождения. |
Его
циркуляция по контуру дает величину
э. д. с, индуцируемой в контуре:
Выберем нормаль так, как показано на рис. 61.1.
|
Тогда при вычислении циркуляции нужно обходить контур по часовой стрелке и соответственно выбирать направление векторов dl.
|
||||||||||||||||
|
Осуществим
в полученном выражении циклическую
перестановку сомножителей, после чего
умножим и разделим его на dt
Закон Фарадея можно сформулировать таким образом: э.д.с. электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром.
|
Этот закон является универсальным: э.д.с. не зависит от способа изменения магнитного потока. Э.д.с. электромагнитной индукции выражается в вольтах. Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим
Мы
получили, что эдс индукции и фоток
имеют противоположные знаки. Единицей
потока магнитной индукции в СИ служит
в е б е р (Вб), который представляет
собой поток через поверхность в 1 м2,
пересекаемую нормальными к ней линиями
магнитного поля с В,
равной 1 Тл. При скорости изменения
потока, равной 1 Вб/с, в кон-туре
индуцируется э. д. с, равная 1 В. В
гауссовой системе формула имеет вид
|
23. Явление самоиндкуции. Индуктивность проводников. Индуктивность соленоида - пустого и заполненного веществом. Электрический
ток, текущий в любом контуре, создает
пронизывающий этот контур магнитный
поток
В
соответствии с законом Био — Савара
магнитная индукция В пропорциональна
силе тока, вызвавшего поле. Отсюда
вытекает, что ток I
и создаваемый им магнитный поток
|
||||||||||||||||
|
Коэффициент пропорциональности L между силой тока и полным магнитным потоком называется индуктивностью контура. Линейная
зависимость
Cлед. индуктивность L зависит от геометрии контура (т. е. его формы и размеров), а также от магнитных свойств (µ) окружающей контур среды. Если контур жесткий и поблизости от него нет ферромагнетиков, индуктивность L является постоянной величиной.
|
За
единицу индуктивности в СИ принимается
индуктивность такого проводника, у
которого при силе тока в нем в 1 А
возникает сцепленный с ним полный
поток В гауссовой системе индуктивность имеет размерность длины. В соответствии с этим единицу индуктивности в этой системе называют сантиметром. Вычислим индуктивность соленоида. Возьмем соленоид такой длины, чтобы его можно было практически считать бесконечным. При
протекании по нему тока I
внутри соленоида возбуждается
однородное поле, индукция которого
равна
|
Поток через каждый из витков равен Ф=BS, а полный
магнитный поток, сцепленный с соленоидом,
где
l
— длина соленоида (которая предполагается
очень большой), S — площадь поперечного
сечения, n
— число витков на единицу длины
(произведение nl дает полное число
витков N).
Сопоставление формул
|
||||||||||||||||
|
Есди
соленоид заполнен веществом с магнитной
проницаемостью µ, то при заданном токе
I
магнитная индукция возрастает в µ
раз, и след. индуктивность длинного
соленоида, заполненного веществом
При изменениях силы тока в контуре возникает э. д. с. Самоиндукции εs., равна
|
Если при изменениях силы тока индуктивность остается постоянной (что возможно лишь при отсутствии ферромагнетиков), выражение для э. д. с. самоиндукции имеет вид
|
24. Энергия магнитного поля в соленоиде. Плотность энергии магнитного поля. Рассмотрим
цепь, изображенную на рис. 67.1 (Сав.
195). При замкнутом ключе в соленоиде
установится ток I,
который обусловит магнитное поле,
сцепленное с витками соленоида. Если
разомкнуть ключ, то через сопротивление
R будет некоторое время течь постепенно
убывающий ток, поддерживаемый
возникающей в соленоиде э. д. с.
самоиндукции. Работа, совершаемая
этим током за время dt, равна
Если
индуктивность соленоида не зависит
от I
(L=const), то
|
||||||||||||||||
|
Проинтегрировав
это выражение по l
в пределах от первоначального значения
I
до нуля, получим работу, совершаемую
в цепи за все время, в течение- которого
происходит исчезновение магнитного
поля,
тается заключить, что магнитное поле является носителем энергии, за счет которой и совершается работа. |
Таким
образом, мы приходим к выводу, что
проводник с индуктивностью L, по
которому течет ток силы I,
обладает энергией
которая локализована в возбуждаемом током магнитном поле. Выразим
энергию магнитного поля через величины,
характеризующие само поле. В случае
очень длинного (практически бесконечного)
соленоида
|
Магнитное
поле бесконечно длинного соленоида
однородно и отлично от нуля только
внутри соленоида. Следовательно,
энергия локализована внутри соленоида
и распределена по его объему с постоянной
плотностью w,
которую можно найти, разделив W на V.
Произведя это деление, получим
Плотность
энергии магнитного поля можно записать
в виде
Зная
плотность энергии поля в каждой точке,
можно найти энергию поля, заключенную
в любом объеме V. Для этого нужно
вычислить интеграл
|
||||||||||||||||
|
25 Квазистационарный переменный электрический ток. Условие квазистационарности. Закон Ома для цепей квазистационарных токов. Активное и реактивное (емкостное, индуцированное) сопротивления, их зависимость от частоты тока. В цепях постоянного тока распределение электрических зарядов на проводниках и токов на участках цепи стационарно, то есть неизменно во времени. Если на каком-то участке цепи происходят изменения силы тока или напряжения, то другие участки цепи могут «почувствовать» эти изменения только через некоторое время, которое по порядку величины равно времени τ распространения электромагнитного возмущения от одной точки цепи к другой. |
Так
как электромагнитные возмущения
распространяются с конечной скоростью,
равной скорости
света c , то
Квазистационарные процессы можно исследовать с помощью законов постоянного тока, если применять эти законы к мгновенным значениям сил токов и напряжений на участках цепи. . |
Из-за огромного значения скорости света время установления электрического равновесия в цепи оказывается весьма малым. Поэтому к квазистационарным можно отнести многие достаточно быстрые в обычном смысле процессы. Например, быстрые колебания в радиотехнических цепях с частотами порядка миллиона колебаний в секунду и даже выше очень часто еще можно рассматривать как квазистационарные Простыми примерами квазистационарных процессов могут служить процессы, происходящие в RC- и RL-цепях при подключении и отключении источника постоянного тока.
|
||||||||||||||||
|
При
рассмотрении электрических колебаний
приходится иметь дело с токами,
изменяющимися со временем. Токи,
удовлетворяющие такому условию,
называются квазистационарными. Для
периодически изменяющихся токов
условие квазистационарности имеет
вид
Квазистационарный ток - относительно медленно изменяющийся переменный ток, для мгновенных значений которого с достаточной точностью выполняются законы постоянных токов (прямая пропорциональность между током и напряжением. Подобно постоянным токам, К. т. имеет одинаковую силу тока во всех сечениях неразветвлённой цепи |
. Однако при расчёте К. т. (в отличие от расчёта цепей постоянного тока) необходимо учитывать возникающую при изменениях тока эдс индукции. Индуктивности, ёмкости, сопротивления ветвей цепи К. т. могут считаться сосредоточенными параметрами. Соотношения, связывающие амплитуды переменных токов и напряжений на резисторе, конденсаторе и катушке индуктивности:
. |
Соотношения (*) выражают закон Ома для участка цепи переменного тока, содержащего один из элементов R, L и C.
Физические
величины R,
|
||||||||||||||||
|
26. Электрический колебательный контур. Частота собственных колебаний тока в контуре. Добротность колебательного контура. В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур (рис. 5.2.1).
Рисунок 5.2.1. Последовательный RLC-контур.
. |
Когда
ключ K находится в положении 1, конденсатор
заряжается до напряжения
иметь колебательный характер. Закон Ома для замкнутой RLC-цепи, не содержащей внешнего источника тока, записывается в виде
где |
В правой части этого соотношения стоит ЭДС самоиндукции катушки. Уравнение, описывающее свободные колебания в RLC-контуре, может быть приведено к следующему виду, если в качестве переменной величины выбрать заряд конденсатора q(t):
|
||||||||||||||||
|
Рассмотрим сначала случай, когда в контуре нет потерь электромагнитной энергии (R = 0). Тогда
Здесь
принято обозначение:
В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими, то есть происходят по закону
|
Параметры L и C колебательного контура определяют только собственную частоту свободных колебаний
Амплитуда q0 и начальная фаза φ0 определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия. В частности, для процесса колебаний, который начнется в контуре (рис. 5.2.1) после переброса ключа K в положение 2, q0 = Cε, φ0 = 0.
|
При свободных колебаниях происходит периодическое превращение электрической энергии Wэ, запасенной в конденсаторе, в магнитную энергию Wм катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается неизменной:
Все реальные контура содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в джоулево тепло, и колебания становятся затухающими (рис. 5.2.3).
|
||||||||||||||||
|
Рисунок 5.2.3. Затухающие колебания в контуре. Затухающие колебания в электрическом контуре аналогичны затухающим колебаниям груза на пружине при наличии вязкого трения, когда сила трения изменяется прямо пропорционально скорости тела: Fтр = – βυ. Коэффициент β в этой формуле аналогичен сопротивлению R в электрическом контуре. Уравнение свободных колебаний в контуре при наличии затухания имеет вид
|
Физическая величина δ = R / 2L называется коэффициентом затухания. Решением этого дифференциального уравнения является функция
которая
содержит множитель exp (–δt), описывающий
затухание колебаний. Скорость затухания
зависит от электрического сопротивления
R контура. Интервал времени
.
|
Добротности Q колебательной системы:
где N – число полных колебаний, совершаемых системой за время затухания τ. Добротности Q любой колебательной системы, способной совершать свободные колебания, может быть дано энергетическое определение:
|
||||||||||||||||
|
Для RLC-контура добротность Q выражается формулой
Добротность электрических контуров, применяемых в радиотехнике, обычно порядка нескольких десятков и даже сотен. Следует отметить, что собственная частота ω свободных колебаний в контуре с не очень высокой добротностью несколько меньше собственной частоты ω0 идеального контура с теми же значениями L и C. Но при Q ≥ (5 – 10) этим различием можно пренебречь
|
27. Вынужденные колебания тока в LCR контуре, уравнение их описывающее. Явление электрического резонанса. Процессы, возникающие в электрических цепях под действием внешнего периодического источника тока, называются вынужденными колебаниями. Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Периодический внешний источник обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на наличие неизбежных потерь.
|
Особый интерес представляет случай, когда внешний источник, напряжение которого изменяется по гармоническому закону с частотой ω, включен в электрическую цепь, способную совершать собственные свободные колебания на некоторой частоте ω0. Если частота ω0 свободных колебаний определяется параметрами электрической цепи, то установившиеся вынужденные колебания всегда происходят на частоте ω внешнего источника. Для установления стационарных вынужденных колебаний необходимо некоторое время Δt после включения в цепь внешнего источника. Это время по порядку величины равно времени τ затухания свободных колебаний в цепи.
|
||||||||||||||||
|
Электрические цепи, в которых происходят установившиеся вынужденные колебания под действием периодического источника тока, называются цепями переменного тока.
Р
|
Вынужденные колебания в контуре. Предполагается, что для электрической цепи, изображенной на рис. 5.3.1, выполнено условие квазистационарности. Поэтому закон Ома можно записать для мгновенных значений токов и напряжений:
Величина
|
Уравнение
вынужденных колебаний можно записать
в виде
Частное
решение уравнения имеет вид
Можно
получить формулы для I Из выражения для I0 видно, что амплитуда тока принимает максимальное значение при условии
или
|
||||||||||||||||
|
Явление возрастания амплитуды колебаний тока при совпадении частоты ω внешнего источника с собственной частотой ω0 электрической цепи называется электрическим резонансом. При резонансе
При последовательном резонансе (ω = ω0) амплитуды UC и UL напряжений на конденсаторе и катушке резко возрастают:
Добротность RLC-контура:
|
28. Электромангитное поле. Вихревое электрическое поле. Первое уравнение Максвелла в интегральной форме как обобщение закона электромагнитной индукции Фарадея. Электромагнитное поле – это неразрывно связанные между собой и порождающие друг друга переменные электрическое и магнитное поля. Впервые понятие “электромагнитное поле” было введено и математически строго описано Джеймсом Клерком Максвеллом. Уравнения Максвелла были опубликованы им в 1873 году в книге “Трактат об электричестве и магнетизме”, т.е. почти 130 лет тому назад.
|
Громоздкий механистический вывод отдельных уравнений был опубликован в его более ранних статьях. В “Трактате” же Максвелл их вывел с помощью аппарата векторного анализа, показав, что переменные электрическое и магнитное поля находятся в неразрывной взаимосвязи, совокупность которых представляет собой единое электромагнитное поле. Основными векторами, характеризующими электромагнитное поле, являются индукция B и напряженность H магнитного поля, смещение D и напряженность E электрического поля и плотность электрического тока J. В указанных современных обозначениях система уравнений Максвелла, заключающая в себе теорию электромагнитного поля, записывается следующим образом. |
||||||||||||||||
|
В
60-х годах XIX в. английский ученый Дж.
Максвелл (1831-1879) обобщил экспериментально
установленные законы электрического
и магнитного полей и создал законченную
единую теорию
электромагнитного поля.
Она позволяет решить основную
задачу электродинамики:
найти характеристики электромагнитного
поля заданной системы электрических
зарядов и токов. Согласно
закону электромагнитной индукции
Фарадея, всякое изменение магнитного
поля во времени
|
Многочисленные
опыты показали, что ЭДС
|
Максвелл
выдвинул гипотезу, что всякое
переменное магнитное поле возбуждает
в окружающем пространстве вихревое
электрическое поле
Уравнение (5.1) называют первым уравнением Максвелла. Смысл его заключается в том, что изменяющееся магнитное поле порождает вихревое электрическое, а последнее в свою очередь вызывает в окружающем диэлектрике или вакууме изменяющееся магнитное поле. |
||||||||||||||||
|
Поскольку магнитное поле создается электрическим током, то, согласно Максвеллу, вихревое электрическое поле следует рассматривать как некоторый ток, который протекает как в диэлектрике, так и в вакууме. Максвелл назвал этот ток током смещения. Механизм тока смещения будет рассмотрен ниже.
Можно
показать, что циркуляция вектора
|
29. Гипотеза Максвелла о токах смещения. Второе уравнение Максвелл как обобщение о циркуляции вектора магнитной индукции. Ток смещения введен Максвеллом для установления количественных соотношений между переменным электрическим полем и вызываемым им вихревым магнитным полем. Поскольку магнитное поле создается электрическим током, то, согласно Максвеллу, вихревое электрическое поле следует рассматривать как некоторый ток, который протекает как в диэлектрике, так и в вакууме. Максвелл назвал этот ток током смещения.
|
По
Максвеллу полный ток в цепи всегда
замкнут, т.е. на концах проводников
обрывается лишь ток проводимости, а
в диэлектрике (вакууме) между концами
проводника имеется ток смещения,
который замыкает ток проводимости.
Введя понятие полного тока, Максвелл
обобщил теорему о циркуляции вектора
Уравнение (5.6) называется вторым уравнением Максвелла в интегральной форме. Оно представляет собой обобщенный закон полного тока и выражает основное положение электромагнитной теории: токи смещения создают такие же магнитные поля, как и токи проводимости.
|
||||||||||||||||
|
Созданная Максвеллом единая макроскопическая теория электромагнитного поля позволила с единой точки зрения не только объяснить электрические и магнитные явления, но предсказать новые, существование которых было впоследствии подтверждено на практике (например, открытие электромагнитных волн). Обобщая рассмотренные выше положения, приведем уравнения, составляющие основу электромагнитной теории Максвелла. Теорема о циркуляции вектора напряженности магнитного поля:
|
Это уравнение показывает, что магнитные поля могут создаваться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями
Для
полного описания явлений в электрических
и магнитных полях к уравнениям Максвелла
надо добавить теорему Гаусса, а также
выражения, связывающие напряженности
поля и индукции в однородных средах:
|
где
т.е. источниками магнитного поля в данном случае являются только токи проводимости, а источниками электрического поля – только электрические заряды. В этом частном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрические и магнитные поля
|
||||||||||||||||
|
30. Плоская электромагнитная волна, ее основные характеристики. Волновые уравнения и их решения. Скорость э-м волн. Электромагнитные волны, электромагнитные колебания, распространяющиеся в пространстве с конечной скоростью. Существование Электромагнитные волны было предсказано М. Фарадеем в 1832. Дж. Максвелл в 1865 теоретически показал, что электромагнитные колебания не остаются локализованными в пространстве, а распространяются в вакууме со скоростью света с во все стороны от источника. Из того обстоятельства, что скорость распространения Электромагнитные волны в вакууме равна скорости света, Максвелл сделал вывод, что свет представляет собой Электромагнитные волны
|
В 1888 максвелловская теория Электромагнитные волны получила подтверждение в опытах Г. Герца, что сыграло решающую роль для её утверждения. Теория Максвелла позволила единым образом подойти к описанию радиоволн, света, рентгеновских лучей и гамма-излучения. Оказалось, что это не излучения различной природы, а Электромагнитные волны с различной длиной волны. Частота w колебаний электрического Е и магнитного Н полей связана с длиной волны l соотношением: l= 2pс/w Радиоволны, рентгеновские лучи и g-излучение находят своё место в единой шкале Электромагнитные волны (рис.), причём между соседними диапазонами шкалы Электромагнитные волны нет резкой границы. |
Особенности Электромагнитные волны, законы их возбуждения и распространения описываются Максвелла уравнениями. Если в какой-то области пространства существуют электрические заряды е и токи I, то изменение их со временем t приводит к излучению Электромагнитные волны
|
||||||||||||||||
|
На скорость распространения Электромагнитные волны существенно влияет среда, в которой они распространяются. Электромагнитные волны могут испытывать преломление, в реальных средах имеет место дисперсия волн, вблизи неоднородностей наблюдаются дифракция волн, интерференция волн (прямой и отражённой), полное внутреннее отражение и другие явления, свойственные волнам любой природы. Пространств, распределение электромагнитных полей, временные зависимости E (t) и H (t), определяющие тип волн (плоские, сферические и др.), вид поляризации и другие особенности Электромагнитные волны задаются, с одной стороны, характером источника излучения, и с другой — свойствами среды, в которой они распространяются.
|
В случае однородной и изотропной среды, вдали от зарядов и токов, создающих электромагнитное поле, уравнения Максвелла, приводят к волновым уравнениям
:
Е = E0 cos (kr — wt + j) Н = H0 cos (kr — wt + j). Здесь e — диэлектрическая проницаемость, µ— магнитная проницаемость среды, E0 и H0 — амплитуды колебаний электрических и магнитных полей, w — частота этих колебаний, j — произвольный сдвиг фазы, k — волновой вектор, r — радиус-вектор точки;.
|
Если
среда неоднородна или содержит
поверхности, на которых изменяются
её электрические либо магнитные
свойства, или если в пространстве
имеются проводники, то тип возбуждаемых
и распространяющихся Электромагнитные
волны
может существенно отличаться от
плоской линейно-поляризованной волны.
Волновой вектор
Длина
волны
|
||||||||||||||||
|
В
изотропном пространстве скорость
распространения гармонических
Электромагнитные
волны,
т. e. фазовая скорость
|
31. Перенос энергии электромагнитной волной . Вектор плотности потока энергии - вектор Умова-Пойтинга. Электромагнитные волны переносят энергию. Плотность потока энергии можно получит, умножив плотность энергии на скорость волны. Если волна распространяется в вакууме, то ее скорость рана скорости света с. Плотность энергии э-м поля состоит из плотности энергии магнитного поля и электрического поля
|
В данной точке пространства векторы Е и Н изменяются в одной фазе. Учтя, что в вакууме ε=µ=1, найдем соотношение меду Е и н
|
||||||||||||||||
|
Умножив
полученное выражение на с получим
модуль плотности потока энергии
где E и H — вектора напряжённости электрического и магнитного полей соответственно. (в комплексной форме)
|
Этот вектор по модулю равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии волны. Поскольку тангенциальные к границе раздела двух сред компоненты E и H непрерывны, то вектор S непрерывен на границе двух сред.
Плотность
количества движения (импульса)
электромагнитного
поля
определяется вектором
|
32. Плоская и сферическая электромагнитная волна : амплитуда, частота, период, длина волны, фаза. Электромагнитные колебания - периодические или почти периодические изменения заряда, силы тока, магнитной индукции, напряжения и других электрических и магнитных величин.
Амплитуда
поля не может непосредственно
наблюдаться или измеряться, так как
поле очень быстро меняется во времени
с частотой
|
||||||||||||||||
|
Поэтому
регистрируется лишь усредненная во
времени величина - интенсивность
поля
Из
уравнений Максвелла следует, что
интенсивность пропорциональна квадрату
амплитуды поля
Фаза колебаний - физическая величина, определяющая при заданной амплитуде состояние колебательной системы в любой момент времени.
|
Фаза колебаний выражается в угловых единицах или долях периода колебаний. Длина волны λ- расстояние на которое распространяется волна за время, равное периоду колебаний
Частота
колебаний
Амплитуда - максимальное значение периодически изменяющейся величины.
|
Период колебаний - время одного полного колебания. Частота колебаний - количественная характеристика периодического колебательного процесса, равная числу полных колебаний, совершаемых в единицу времени. Частота колебаний: - обратно пропорциональна периоду колебаний; - измеряется в герцах. Плоские волны (plane waves) называются так потому, что они имеют плоские волновые фронты (рис.1.4.2).
|
||||||||||||||||
|
Волновой
фронт
- это поверхность в пространстве, на
которой или фаза имеет одинаковые
значения:
Различным
значениям постоянной
Направление распространения света перпендикулярно волновым фронтам, как показано на рис.1.4.2.
|
Уравнение плоской волны имеет следующий вид:
Для плоской волны амплитуда постоянна, меняется только фаза, который можно записать как уравнение плоскости: Плоские волны замечательны тем, что любое сложное поле можно представить в виде совокупности плоских волн. Поэтому эти волны являются универсальным базисом для описания световых полей. Сферические волны (spherical waves) имеют волновой фронт в виде концентрических сфер (рис.1.4.3).
|
Уравнение сферической волны:
Уравнение эйконала сферической волны:
где
Сферические волны так же, как и плоские, могут быть использованы для представления сложных полей, кроме того, плоские волны можно считать частным случаем сферической волны с бесконечно малой кривизной волнового фронта. |
||||||||||||||||
|
Шкала электромагнитных волн
Электромагнитные
волны классифицируются по длине волны
Рассмотрим понятие спектра электромагнитных волн. Спектром электромагнитных волн называется полоса частот электромагнитных волн, существующих в природе. Спектр электромагнитного излучения в порядке увеличения частоты составляют: |
1) Радиоволны; 2) Инфракрасное излучение; 3) Световое излучение; 4) Рентгеновское излучение; 5) Гамма излучение. Различные участки электромагнитного спектра отличаются по способу излучения и приёма волн, принадлежащих тому или иному участку спектра. По этой причине, между различными участками электромагнитного спектра нет резких границ. Радиоволны. Радиоволны представляют собой электромагнитные волны, длины которых превосходят 0.1мм( частота меньше 3 1012гц = 3000 Ггц).
|
Радиоволны делятся на: 1. Сверхдлинные волны с длиной волны больше 10км( частота меньше 3 104гц=30кгц); 2. Длинные волны в интервале длин от10км до 1км( частота в диапазоне 3 104 гц -3 105гц=300кгц); 3. Средние волны в интервале длин от1км до 100м(частота в диапазоне 3 105 гц -3106гц=3мгц); 4. Короткие волны в интервале длин волн от 100м до 10м (частота в диапазоне 3106гц-3107гц=30мгц); 5. Ультракороткие волны с длиной волны меньше 10м(частота больше 3107гц=30Мгц).
|
||||||||||||||||
|
Ультракороткие волны в свою очередь делятся на : а) метровые волны; б) сантиметровые волны; в) миллиметровые волны; г) микрометровые. Волны с длиной волны меньше, чем 1м(частота меньше чем 300мгц) называются микроволнами или волнами сверхвысоких частот(СВЧ - волны). Инфракрасное и световое излучения. Инфракрасное, световое, включая ультрафиолетовое, излучения составляют оптическую область спектра электромагнитных волн в широком смысле этого слова. Близость участков спектра перечисленных волн обусловило сходство методов и приборов, применяющихся для их исследования и практического применения. |
Исторически для этих целей применяли линзы, дифракционные решетки, призмы, диафрагмы, оптически активные вещества, входящие в состав различных оптических приборов (интерферометров, поляризаторов, модуляторов и пр.). С другой стороны излучение оптической области спектра имеет общие закономерности прохождения различных сред, которые могут быть получены с помощью геометрической оптики, широко используемой для расчетов и построения, как оптических приборов, так и каналов распространения оптических сигналов. Оптический спектр занимает диапазон длин электромагнитных волн в интервале от 210-6м= 2мкм до 10-8м=10нм (по частоте от1.51014гц до 31016гц). |
Верхняя граница оптического диапазона определяется длинноволновой границей инфракрасного диапазона, а нижняя коротковолновой границей ультрафиолета
Ширина
оптического диапазона по частоте
составляет примерно 18 октав1,
из которых на оптический диапазон
приходится примерно одна октава( В оптической части спектра становятся существенными явления, обусловленные атомистическим строением вещества. По этой причине наряду с волновыми свойствами оптического излучения проявляются квантовые свойства.
|
||||||||||||||||
|
|
Рентгеновское излучение возникает при торможении быстрых заряженных частиц (электронов, протонов и пр.), а также в результате процессов, происходящих внутри электронных оболочек атомов.
Гамма
излучение является следствием явлений,
происходящих внутри атомных ядер, а
также в результате ядерных реакций.
Граница между рентгеновским и гамма
излучением определяются условно по
величине кванта энергии
Рентгеновское излучение составляют электромагнитные волны с длиной от50 нм до 10-3нм, что соответствует энергии квантов от 20эв до 1Мэв. Гамма излучение составляют электромагнитные волны с длиной волны меньше 10-2нм, что соответствует энергии квантов больше 0.1Мэв. |
|||||||||||||||||

 .
.
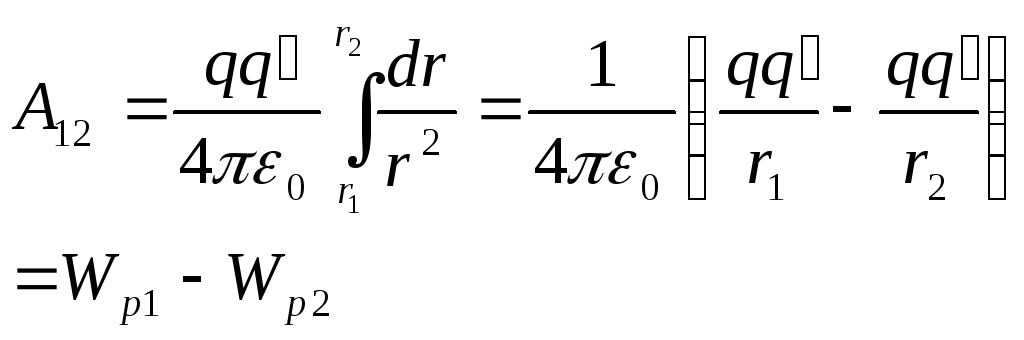 .
.
 .
.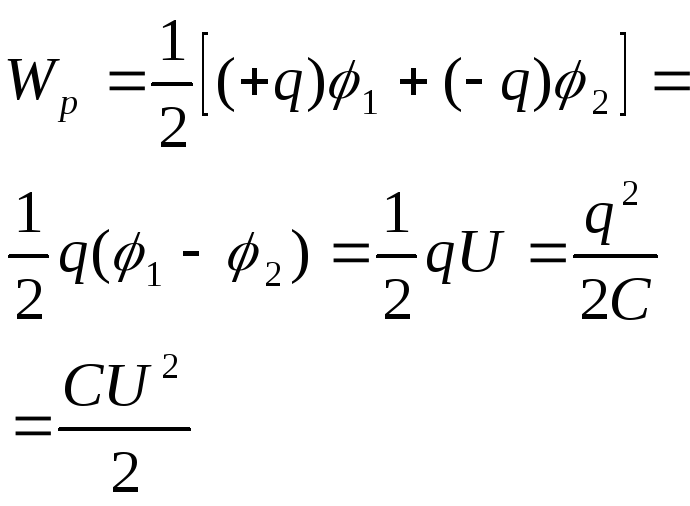 .
. ,
,
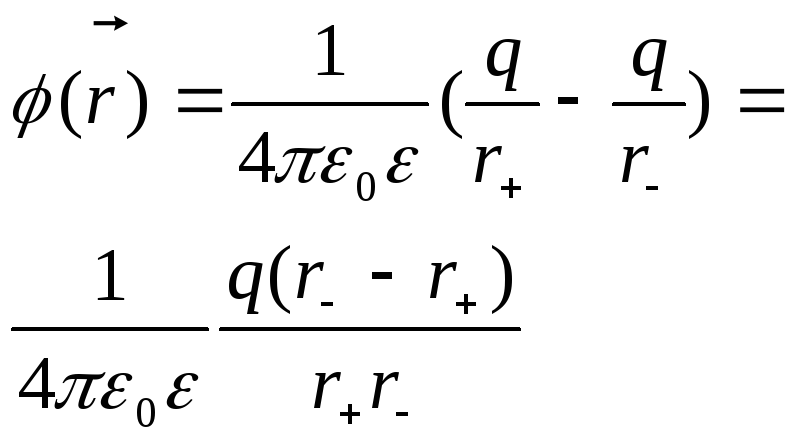 .
Произведение
.
Произведение
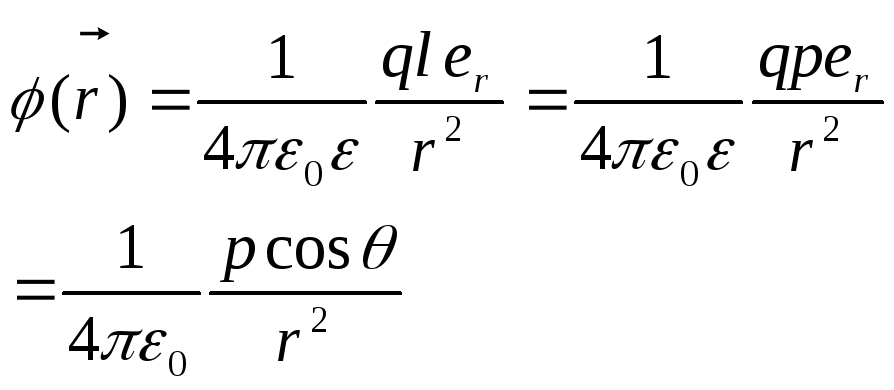 ,
т.к
,
т.к
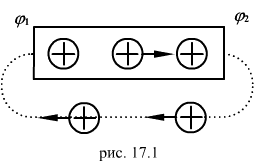
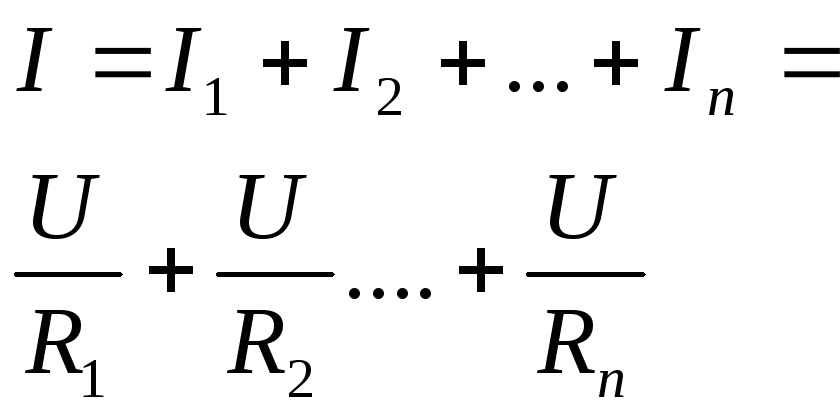 ,
учитывая закон Ома для участка цепи,
получим для параллельного соединения
проводников следующую формулу
,
учитывая закон Ома для участка цепи,
получим для параллельного соединения
проводников следующую формулу
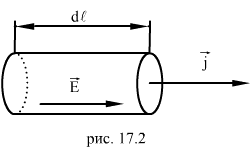
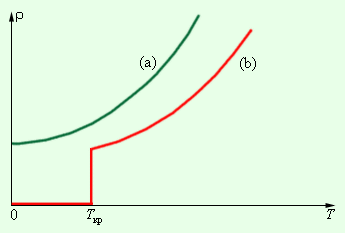

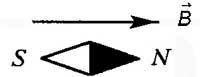
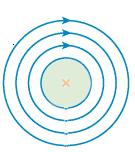
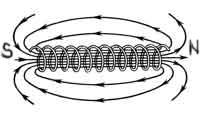


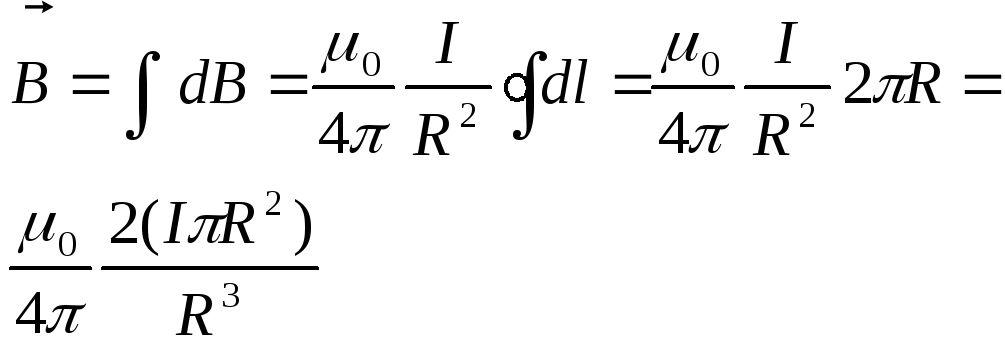 Выражение
в скобках равно модулю дипольного
магнитного момента pm.
Следовательно, магнитная индукция в
центре кругового тока имеет величину
Выражение
в скобках равно модулю дипольного
магнитного момента pm.
Следовательно, магнитная индукция в
центре кругового тока имеет величину
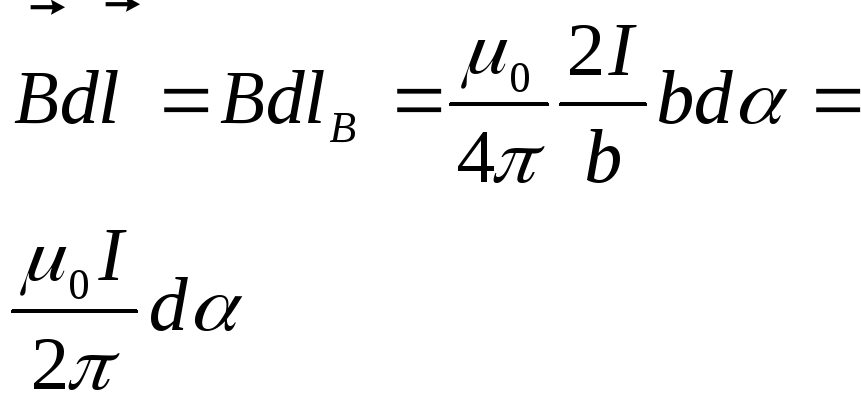
 еоднородное
магнитное поле ориентирует + притягивает
или отталкивает рамку с током.
еоднородное
магнитное поле ориентирует + притягивает
или отталкивает рамку с током.
 ак,
в магнитном поле прямого проводника
с током (оно неоднородно) рамка с током
ориентируется вдоль радиуса магнитной
линии и притягивается или отталкивается
от прямого проводника с током в
зависимости от направления токов.
ак,
в магнитном поле прямого проводника
с током (оно неоднородно) рамка с током
ориентируется вдоль радиуса магнитной
линии и притягивается или отталкивается
от прямого проводника с током в
зависимости от направления токов.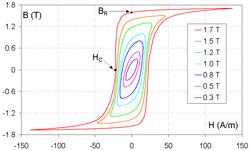
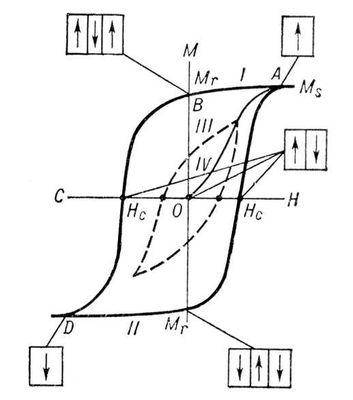 Под действием внешнего магнитного
поля число и размеры доменов,
намагниченных по полю, увеличиваются
за счёт др. доменов. Кроме того, магнитные
моменты отдельных доменов могут
поворачиваться по полю. В
результате магнитный
момент
образца увеличивается.
Под действием внешнего магнитного
поля число и размеры доменов,
намагниченных по полю, увеличиваются
за счёт др. доменов. Кроме того, магнитные
моменты отдельных доменов могут
поворачиваться по полю. В
результате магнитный
момент
образца увеличивается.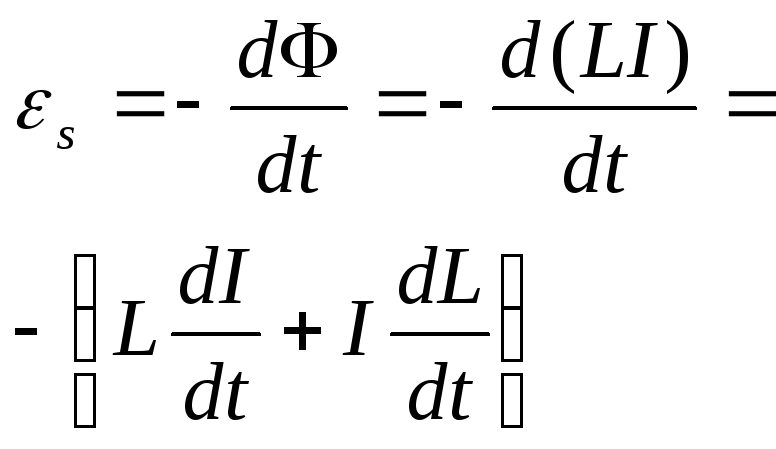
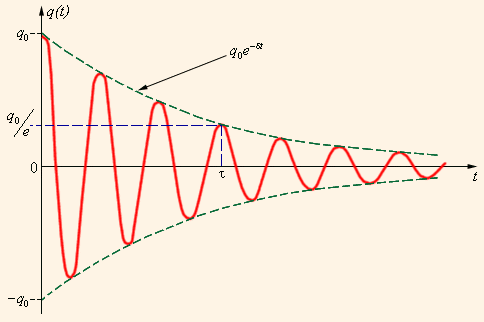
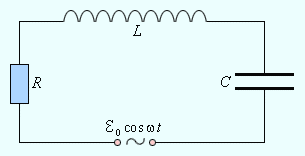 ассмотрим
последовательный колебательный
контур, то есть RLC-цепь, в которую
включен источник тока, напряжение
которого изменяется по периодическому
закону (рис. 5.3.1): e(t) =
ассмотрим
последовательный колебательный
контур, то есть RLC-цепь, в которую
включен источник тока, напряжение
которого изменяется по периодическому
закону (рис. 5.3.1): e(t) =  (5.1)
(5.1)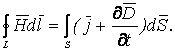 (5.6)
(5.6)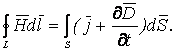
 .
.
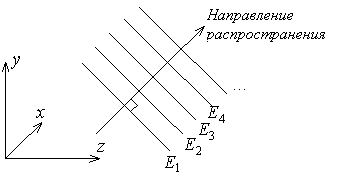 Рис.1.4.2.
Плоские волны.
Рис.1.4.2.
Плоские волны. Рис.1.4.3.
Сферические волны.
Рис.1.4.3.
Сферические волны.
