2.4 Инструкция пользователя
При запуске программы на экране появляется окно программы, изображенное на рисунке 2.6, которое разделено на две части. В левой части расположены поля для ввода входных данных.
N – количество состояний системы
M – математическое ожидание времени обработки информации в систему
D – дисперсия времени и передачи информации в систему
S – время опроса датчиков
i – количество итераций
j – частота сбора информации для построения графика АС
t – время задержки графика на экране
Рисунок
2.6 Ввод исходных данных
В
нижнем левом углу расположены кнопки
для запуска программы на исполнение с
различными условиями. Они представлены
на рисунке 2.7.
Рисунок 2.7 Кнопки запуска программы
Ниже расположены поля выбора прорисовки сетки, применения опроса датчиков, прорисовка линий и вывода значений, представленные на рисунке 2.8.
Рисунок
2.8 Поля выбора настроек отображения
В правой части окна программы расположены поля для вывода на экран результатов работы в виде графиков и гистограмм.
Вводим исходные данные в поля исходных данных. Окно ввода данных представлено на рисунке 2.9. Сначала выбираем количество состояний, в которых может находиться объект, при этом появляется таблица с количеством строк, равным количеству состояний. В этом окне нужно ввести математическое ожидание и дисперсию времени нахождения объекта в каждом из состояний. Нажав кнопку «Сохранить» при следующем запуске программы, их можно будет не вводить повторно.
Далее вводим данные для времени, затрачиваемого на обработку информации в окошки M, D. Вводим данные о количестве итераций i, частоте сбора информации для построения графика АС j, времени задержки графика на экране t.
Рисунок 2.9 Окно ввода настроек
Запускаем программу на исполнение нажатием одной из кнопок в поле «Без датчика», что означает непрерывный сбор информации. Графическое изображение этих кнопок на рисунке 2.10.
Рисунок
2.10 Кнопки запуска программы с непрерывным
опросом датчиков
Поле
«с датчиком» изображено на рисунке
2.11.
Рисунок 2.11 Кнопки запуска программы с циклическим опросом датчиков
В
результате работы программы в правой
части появятся графики ξ(t)
изменения состояния объекта и случайного
процесса ϕ(t)
изменения состояния модели, представленные
на рисунке 2.12.
Рисунок 2.12 Результаты работы программы
После
вывода на экран всех i
наборов графиков появится график функции
совпадения Гс(t).
Он изображен на рисунке 2.13.
Рисунок 2.13 График функции совпадения
Двойной
клик левой кнопкой мыши на график функции
совпадения выводит этот график в
отдельное окно. График функции совпадения,
представленный в отдельном окне,
изображен на рисунке 2.14. 
Рисунок 2.14 График функции совпадения, представленный в отдельном окне
Глава 3 контрольные примеры
3.1 Оценка старения информации о пассажирского движении локомотивов на Большом окружном кольце мжд
Рисунок
3.1 Схема БМО
Большое кольцо Московской железной дороги (БК МЖД) — окружная железная дорога вокруг Москвы, проходящая по территории Московской и Владимирской областей на расстоянии 30—120 км от МКАД. Предназначена для осуществления пассажирских перевозок и грузовых транзитных перевозок между всеми магистральными железнодорожными направлениями столицы. Эксплуатационная длина дороги составляет около 584 км.
Для управления локомотивами грузового движения диспетчеру необходимы сведения о местонахождении локомотивов на определенных участках и станциях железной дороги. Эти данные обрабатываются в ИВЦ, контролируются путем фиксации их прибытия, отправления и проследования по контрольным пунктам, которыми являются станции.
Информационной базой для решения задачи является информационная модель дислокации локомотивов. Обновление информации происходит определенное число раз в сутки.
В таблице 3.1 приведены условные (взятые для примера) характеристики времени хода локомотива по участкам стоянок на выделенных для примера станциях. Оценим качество оперативной информации о процессе перемещения локомотива.
Таблиц 3.1 Характеристики времени хода локомотива по участкам и стоянке на станциях
|
№ |
Станции и участки |
Характеристики времени нахождения локомотива на участке или станции | |
|
М (час) |
Ϭ (час) | ||
|
1 |
Александров 1 - Дмитров |
2,1 |
0,7 |
|
2 |
Дмитров |
1,5 |
0,5 |
|
3 |
Дмитров- Кубинка-1 |
3 |
1 |
|
4 |
Кубинка-1 |
1 |
0,3 |
|
5 |
Кубинка-1 - Бекасово-1 |
1 |
0,3 |
|
6 |
Бекасово-1 |
1,8 |
0,6 |
Продолжение таблицы 3.1
|
7 |
Бекасово-1 – Дедково |
2,2 |
0,7 |
|
8 |
Дедково |
2 |
0,6 |
|
9 |
Дедково – Непецино |
2 |
0,6 |
|
10 |
Непецино |
1,5 |
0,5 |
|
11 |
Непецино – Орехово-Зуево |
2,1 |
0,7 |
|
12 |
Орехово-Зуево |
2,3 |
0,8 |
|
13 |
Орехово–Зуево – Александров-1 |
1,9 |
0,6 |
|
14 |
Александров-1 |
1,4 |
0,3 |
Смоделируем в программе этот пример. Зададим период обработки информации равным 1ч.
Считаем, что общая продолжительность операций, связанных с прибытием и обработкой состава в парке прибытия, составляет в среднем 25,8 мин, а среднее время переработки данных о завершении каждой из указанных технологических операций с m = 1.
Для определения значения вероятности kc того, что в произвольный момент времени отображаемое в информации состояние поезда (соответствующее выполняемой над ними технологической операции) адекватно реальному, рассмотрим реализации случайных процессов ξ(t) изменения состояний поезда, случайных процессов ϕ(t) отображаемых в информации состояний поезда.
Обозначим Tdj (j = 1,…,15) – случайное время выполнения j-й технологической операции; Tобр случайное время обработки данных о начале (завершении) выполнения очередной технологической операции. Вероятность того, что в произвольный момент времени отображаемое в информации состояние поезда совпадает с реальным, определяется из следующего соотношения. Так как mtобр << mdj (j = 1,…,15), то
|
|
(3.1) |
Таким образом, для условий примера имеем
Расчет показывает, что степень совпадения отображаемого и реального процессов обработки поезда в ПП невысока.
Проверим программно.
Необходимо
вычислить N’
требуемое количество реализаций.
Вероятность p
первоначально нам неизвестна. Поэтому
для определения количества реализаций
выбираем N0=50,
по результатам N0
реализаций определяем средним значением
функции совпадения
,
которое и примем за вероятностьp.
Для
обеспечения статистической устойчивости,
соответствующие оценки вычисляются
как средние значения по большому
количеству реализаций. В силу центральной
предельной теоремы частота
при достаточно больших N
имеет место распределение, близкое к
нормальному. Поэтому для каждого значения
достоверностью α можно выбрать из таблиц
нормального распределения такую величину
tα,
что точность ε
будет равна [2]:
|
|
(3.2) |
Для α=0,95, tα=1,96. Подставляя вместо дисперсии ее значение получаем:
|
|
(3.3) |
Отсюда
можно определить количество реализаций
N’,
необходимых для получения оценки
с погрешностью ε и достоверность α [2].
|
|
(3.4) |
Рассчитаем N’ и для нашего примера:
Запустим программу для подсчета среднего значения функции совпадения. Количество итераций, при этом, установив равным N = 371.
В
результате получим график функции
совпадения, изображенный на рисунке
3.2.
Рисунок 3.2 График функции совпадения с непрерывным опросом датчиков без прогнозирования
Мы
получили, что среднее значение
=
0,41 (без прогноза), так как мы знаем, что
=0,42,
то можем вычислить погрешность следующим
образом:
Из
полученных результатов видно, что
коэффициент совпадения kс
расходится со средним значением функции
совпадения
не более чем на 5%. При этом, для непрерывного
опроса датчиков с прогнозом среднее
значение функции совпадения равно
= 0,77.
Сравним результаты работы программы (средние значения функции совпадения) в случае циклического опроса датчиков. Время обработки информации зададим равным M = 1ч, период опроса датчиков S = 0,5 ч.
Среднее
значение функции совпадения без
прогнозирования равно
.
График функции представлен на рисунке
3.3.
Рисунок 3.3 График Гс(t) с циклическим опросом датчиков без прогнозирования
Среднее
значение функции совпадения с
прогнозированием
График функции совпадения представлен
на рисунке 3.4.
Рисунок
3.4 График Гс(t)
с циклическим опросом датчиков с
прогнозированием
Уменьшим
время обработки информации до 0,3 часа
(20 мин). Среднее значение функции
совпадения без прогнозирования равно
.
График функции представлен на рисунке
3.5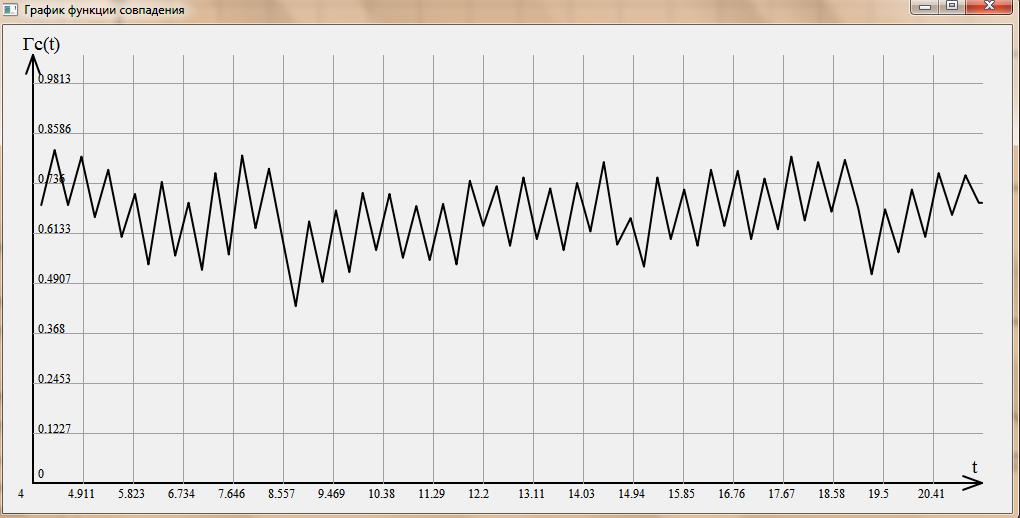
Рисунок 3.5 График функции совпадения с циклическим опросом датчиков с прогнозированием
Среднее
значение функции совпадения с
прогнозированием
График функции совпадения представлен
на рисунке 3.6.
Рисунок
3.6 График Гс(t)
с циклическим опросом датчиков с
прогнозом
Увеличим период опроса датчиков до 3 часов. Время обработки информации оставим прежним: M = 0,3 ч .
Среднее
значение функции совпадения без
прогнозирования равно
.
График функции представлен на рисунке
3.7.
Рисунок
3.7 График Гс(t)
с циклическим опросом датчиков без
прогнозирования
Среднее
значение функции совпадения с
прогнозированием
График функции совпадения представлен
на рисунке 3.8
Рисунок
3.8 График Гс(t)
с циклическим опросом датчиков с
прогнозом
Теперь увеличим время обработки информации M до 1ч. Период опроса датчиков S оставим равным 3 ч.
Среднее
значение функции совпадения без
прогнозирования равно
.
График функции представлен на рисунке
3.9..
Рисунок
3.9 График Гс(t)
с циклическим опросом датчиков без
прогнозирования
Среднее
значение функции совпадения с
прогнозированием
График функции совпадения представлен
на рисунке 3.10.
Рисунок 3.10 График Гс(t) с циклическим опросом датчиков с прогнозированием
Итак, сведем все значения в единую таблицу 3.2 для наглядности и проанализируем полученные результаты.
Таблица 3.2 Результаты работы программы
|
Период опроса датчиков (S) |
Время обработки информации (M) |
Циклический опрос датчиков | |
|
|
Признак «с прогнозом» -«+», «Без прогноза»- «-» | ||
|
3 |
1 |
0,14 |
- |
|
3 |
0,3 |
0,23 |
- |
|
0,5 |
1 |
0,28 |
- |
|
3 |
1 |
0,36 |
+ |
|
3 |
0,3 |
0,44 |
+ |
|
0,5 |
1 |
0,64 |
+ |
|
0,5 |
0,3 |
0,66 |
- |
|
0,5 |
0,3 |
0,77 |
+ |
Вывод:
применение прогнозирования существенно
увеличивает значение функции совпадения
.