12.Матрицы, правило крамера.

Для любой квадратной матрицы может быть найдена величина, называемая определителем.

Определитель — это квадратная таблица чисел или матиматических символов (Δd).

Для матрицы второго порядка определитель вычисляется по формуле:

Разложение по строке или столбцу

Формулы разложения по строке или столбцу:

Первые n формул называются формулами разложения определителя по строке, а вторые n формул называются формулами разложения определителя по столбцу.

В этих формулах - алгебраические дополнения элементов а_ij матрицы А, где M_ij — миноры элементов а_ij матрицы А.

Минором M_ij элемента а_ij матрицы n-го порядка А называется определитель матрицы (n-1)-го порядка, получаемой из матрицы А вычеркиванием i-й строки и j-го столбца, на пересечении которых находится элемент a_ij/

Правило Саррюса

Дописывание двух первых строк или столбцов.

В этом случае считаем так: a11*а22*а33 + а12*а23*31+а13*а21*а32 — а13*а22*а31 — а11*а23*а32 — а12*а21*а33

Пример 32.2

Вычислить определитель двумя способами: с помощью разложения по первой строке и по правилу треугольника:

Решение:

Свойства определителей

Свойство (1) Определитель не изменится, если все строки заменить соответствующими столбцами и наоборот.

Свойство (2) При перестановке двух каких-либо строк или столбцов местами определитель изменяет знак.

Свойство (3) Определитель равен нулю, если он имеет две равные строки (столбца).

Свойство (4) Множитель, общий для всех элементов строки или столбца, можно выносить за знак определителя.

Свойство (5) Если к элементам какой-либо строки или столбца прибавить соответствующие элементы другой строки или столбца, то определитель не изменится.

Следствие из свойств 32.4 и 32.5: Если к элементам какой-либо строки или столбца прибавить соответствующие элементы другой строки или столбца, умноженные на некоторое число, то определитель не изменится.

Свойство (6) Сумма произведений элементов какой-либо строки или столбца на алгебраические дополнения соответствующих элементов другой строки или столбца равна нулю.

Пример 32.3

Вычислить определитель, используя свойства:

Решение:

1. Третью строку умножим на подходящие множители и прибавим к остальным:

получим:

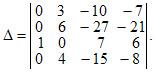
ПРАВИЛО КРАМЕРА

Решение систем уравнений

Пусть имеется система уравнений:

Обозначим через Δ определитель матрицы системы и через Δ_j определитель, который получается из определителя Δ заметой j-го столбца столбцом правых частей системы ( j=1,2,...n).

Теорема 1

Если определитель матрицы отличен от нуля, т.е. Δ ≠0, то система имеет единственное решение, которое находится по формуле: 

Нахождение обратной матрицы

Путь имеется матрица:

Матрица:

13. Теорема Крамера Капелли, метод гаусса

 Теорема. Система из n уравнений с n неизвестными

в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:

, где = detA,  а i – определитель матрицы, получаемой из матрицы системы заменой столбца iстолбцом свободных членов b_i. i = 

Решение систем линейных уравнений методом Крамера.

Пусть нам требуется решить систему линейных алгебраических уравнений   в которой число уравнений равно числу неизвестных переменных и определитель основной матрицы системы отличен от нуля, то есть, .

Пусть - определитель основной матрицы системы, а - определители матриц, которые получаются из А заменой 1-ого, 2-ого, …, n-ого столбца соответственно на столбец свободных членов:

При таких обозначениях неизвестные переменные вычисляются по формулам метода Крамера как . Так находится решение системы линейных алгебраических уравнений методом Крамера.

Пример.

Решите систему линейных уравнений методом Крамера .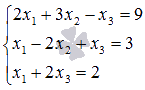

Решение.

Основная матрица системы имеет вид . Вычислим ее определитель (при необходимости смотрите статью определитель матрицы: определение, методы вычисления, примеры, решения):

Так как определитель основной матрицы системы отличен от нуля, то система имеет единственное решение, которое может быть найдено методом Крамера.

Составим и вычислим необходимые определители (определитель получаем, заменив в матрице А первый столбец на столбец свободных членов , определитель - заменив второй столбец на столбец свободных членов, - заменив третий столбец матрицы А на столбец свободных членов):

Находим неизвестные переменные по формулам :

Ответ:

x₁ = 4, x₂ = 0, x₃ = -1.

Основным недостатком метода Крамера (если это можно назвать недостатком) является трудоемкость вычисления определителей, когда число уравнений системы больше трех.

МЕТОД ГАУССА

Решение систем линейных уравнений методом Гаусса.Пусть нам требуется найти решение системы из n линейных уравнений с n неизвестными переменными определитель основной матрицы которой отличен от нуля.

Суть метода Гаусса состоит в последовательном исключении неизвестных переменных: сначала исключается x₁ из всех уравнений системы, начиная со второго, далее исключается x₂из всех уравнений, начиная с третьего, и так далее, пока в последнем уравнении останется только неизвестная переменная x_n. Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называется прямым ходом метода Гаусса. После завершения прямого хода метода Гаусса из последнего уравнения находитсяx_n, с помощью этого значения из предпоследнего уравнения вычисляется x_n-1, и так далее, из первого уравнения находится x₁. Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называется обратным ходом метода Гаусса.

Кратко опишем алгоритм исключения неизвестных переменных.

Будем считать, что , так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменнуюx₁ из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на , к третьему уравнению прибавим первое, умноженное на, и так далее, кn-омууравнению прибавим первое, умноженное на . Система уравнений после таких преобразований примет видгде, а.

К такому же результату мы бы пришли, если бы выразили x₁ через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x₁ исключена из всех уравнений, начиная со второго.

Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке

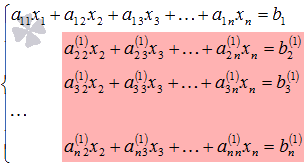
Будем считать, что (в противном случае мы переставим местами вторую строку сk-ой, где ). Приступаем к исключению неизвестной переменнойx₂ из всех уравнений, начиная с третьего.

Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на, и так далее, кn-омууравнению прибавим второе, умноженное на . Система уравнений после таких преобразований примет видгде, а. Таким образом, переменнаяx₂ исключена из всех уравнений, начиная с третьего.

Далее приступаем к исключению неизвестной x₃, при этом действуем аналогично с отмеченной на рисунке частью системы

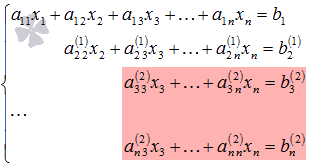
Так продолжаем прямой ход метода Гаусса пока система не примет вид

С этого момента начинаем обратный ход метода Гаусса: вычисляем x_n из последнего уравнения как 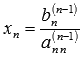, с помощью полученного значенияx_n находим x_n-1 из предпоследнего уравнения, и так далее, находим x₁ из первого уравнения.

Пример.

Решите систему линейных уравнений методом Гаусса.

Решение.

Исключим неизвестную переменную x₁ из второго и третьего уравнения системы. Для этого к обеим частям второго и третьего уравнений прибавим соответствующие части первого уравнения, умноженные на и насоответственно:

Теперь из третьего уравнения исключим x₂, прибавив к его левой и правой частям левую и правую части второго уравнения, умноженные на :

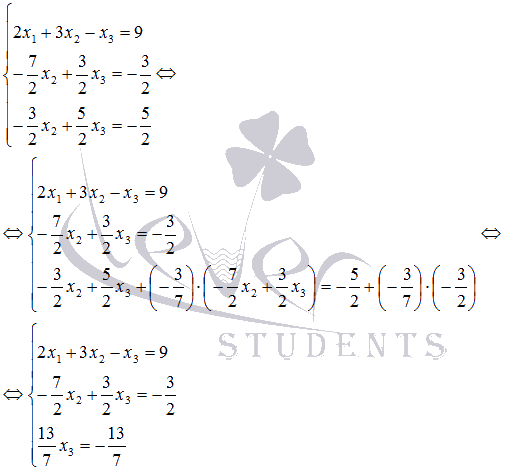
На этом прямой ход метода Гаусса закончен, начинаем обратный ход.

Из последнего уравнения полученной системы уравнений находим x₃:

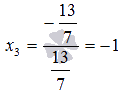
Из второго уравнения получаем .

Из первого уравнения находим оставшуюся неизвестную переменную и этим завершаем обратный ход метода Гаусса .

Ответ:

x₁ = 4, x₂ = 0, x₃ = -1.