5. Скалярное произведение. Свойства высчисления

Скалярным произведением двух векторов называется действительное число, равное произведению длин умножаемых векторов на косинус угла между ними.

Скалярное произведение векторов и будем обозначать как . Тогда формула для вычисления скалярного произведения имеет вид 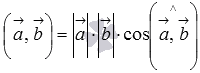, где и - длины векторов и соответственно, а - угол между векторами и .

Из определения скалярного произведения видно, что если хотя бы один из умножаемых векторов нулевой, то .

Вектор можно скалярно умножить на себя. Скалярное произведение вектора на себя равно квадрату его длины, так как по определению .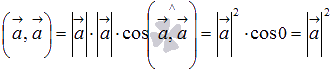

Определение.

Скалярное произведение вектора на себя называется скалярным квадратом.

Формулу для вычисления скалярного произведения 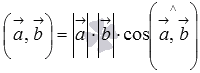можно записать в виде , где - числовая проекция вектора на направление вектора , а - числовая проекция вектора на направление вектора .

Таким образом, можно дать еще одно определение скалярного произведения двух векторов.

Определение.

Скалярным произведением двух векторов и называется произведение длины вектора на числовую проекцию вектора на направление вектора или произведение длины вектора на числовую проекцию вектора на направление вектора .

Это определение эквивалентно первому.

Скалярное произведение в координатах.

Покажем как скалярное произведение вычисляется через координаты векторов в прямоугольной системе координат на плоскости и в пространстве.

Определение.

Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов и .

То есть, для векторов на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид , а для векторов в трехмерном пространстве скалярное произведение в координатах находится как .

Таким образом, мы имеем третье определение скалярного произведения. Покажем, что это определение эквивалентно первому.

Сначала докажем равенства 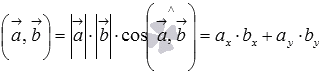для векторов на плоскости, заданных в прямоугольной декартовой системе координат.

Отложим от начала координат (точка О) векторы и . Тогда (при необходимости обращайтесь к статьямоперации над векторами и их свойства и операции над векторами в координатах).

Будем считать точки О, А и В вершинами треугольника ОАВ. По теореме косинусов мы можем записать . Так как 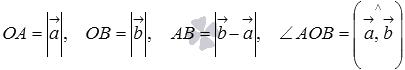, то последнее равенство можно переписать как , а по первому определению скалярного произведения имеем 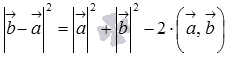, откуда .

Вспомнив формулу вычисления длины вектора по координатам, получаем

Абсолютно аналогично доказывается справедливость равенств для векторов , заданных в прямоугольной системе координат трехмерного пространства.

Формула скалярного произведения векторов в координатах позволяет заключить, что скалярный квадрат вектора равен сумме квадратов всех его координат: на плоскости , в пространстве .

Свойства скалярного произведения.

Для любых векторов и справедливы следующие свойства скалярного произведения:

1. свойство коммутативности скалярного произведения ;

2. свойство дистрибутивности или ;

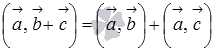3. сочетательное свойство или , где - произвольное действительное число;

4. скалярный квадрат вектора всегда не отрицателен , причем тогда и только тогда, когда вектор нулевой.

Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.

Для примера докажем свойство коммутативности скалярного произведения . По определению и . В силу свойства коммутативности операции умножения действительных чисел, справедливо и , тогда . Следовательно, , что и требовалось доказать.

Аналогично доказываются остальные свойства скалярного произведения.

Следует отметить, что свойство дистрибутивности скалярного произведения справедливо для любого числа слагаемых, то есть, и , откуда следует