
- •1.Системы координат
- •2. Векторы и операци над веторами
- •5. Скалярное произведение. Свойства высчисления
- •Скалярное произведение в координатах.
- •Свойства скалярного произведения.
- •Вычисление скалярного произведения, примеры и решения.
- •6.Вексторное произведение. Свойства вычисления.
- •Свойства векторного произведения
- •7.Смешанное произведение.Свойста вычисления. Свойства смешанного произведения
- •8.Линейные образы на плоскости.
- •9. Кривые 2 порядка
- •10.Линейные образы в пространстве.
- •11. Поверхности второго порядка.
- •12.Матрицы, правило крамера.
- •Разложение по строке или столбцу
- •Правило Саррюса
- •Свойства определителей
- •Решение систем уравнений
- •Нахождение обратной матрицы
- •13. Теорема Крамера Капелли, метод гаусса
- •Решение систем линейных уравнений методом Крамера.
- •14.Фундаментальный набор решений однородной системы уравнений.
- •15.Функции. Последовательность как функция дискретного аргумента.
- •16. Бескоечно большие, бесконечно малые и ограниченные велечины и их свойства.
- •Предел функции
- •4.4. Правила предельного перехода
- •4.5. Бесконечно малые и бесконечно большие величины
- •4.6. Свойства бесконечно малых и бесконечно больших величин и связь между ними
- •Связь бесконечно малой и бесконечно большой величины
- •17.Арифметическое свойство придела.
- •18. Первый замечательный предел.
- •19.Второй замечательный предел.
- •20. Сравнение бесконечно малых величин. Бесконечно малые функции. Сравнение бесконечно малых
- •Сравнение бесконечно малых функций
- •21.Неперывность ффункции, классификация точекк разрыва.
- •22.Производная и ее свойства.
- •Правила дифференцирования
- •Основные формулы дифференцирования.
- •23. Производная сложной и обратной функции.
- •24.Геометрический смысл производной.
- •25. Дефференциал.
- •Геометрический смысл дифференциала
- •26. Теорема лагранжа о конечном приращении.
- •27. Теорема ролля Теорема Ролля
- •28. Теорема ферма Теорема Ферма
- •29.Теорема коши
- •30. Монотонность и экстремумы функции. Применение производной. Монотонность функции, основные понятия и определения
- •Связь монотонности функции с ее производной
- •31. Асимптоты. Точки перегиба. Построение графиков функций
- •32. Логарифмическое дифференцирование.
- •Случай независимой переменной
- •Случай зависимой переменной
- •34. Формула тейлора
- •Формула Тейлора
- •35. Функции нескольких переменных. Непрерывность. Дифференцируемость.
- •36. Повторное дифференцирование.
- •37. Геометрический смысл частных производных.
- •38. Дифференциал функции нескольких переменных.
- •39. Производная по направлению. Градиент.
- •40. Дифференцирование сложной функции нескольких переменных.
- •41. Экстремумы функции нескольких переменных.
- •42. Условные экстремумы. Метод множителей Лагранжа
32. Логарифмическое дифференцирование.

При
дифференцировании показательно степенной
функции ![]() или
громоздких дробных выражений удобно
пользоваться логарифмической производной.
В этой статье мы рассмотрим примеры ее
применения с подробными решениями.
или
громоздких дробных выражений удобно
пользоваться логарифмической производной.
В этой статье мы рассмотрим примеры ее
применения с подробными решениями.
Дальнейшее изложение подразумевает умение пользоваться таблицей производных,правилами дифференцирования и знание формулы производной сложной функции.
Вывод формулы логарифмической производной.
Сначала
производим логарифмирование по
основанию e,
упрощаем вид функции, используя свойства
логарифма, и далее находим производную
неявно заданной функции:
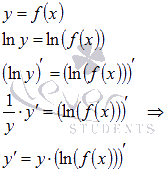
Для примера найдем производную показательно степенной функции x в степени x.
Логарифмирование
дает ![]() .
По свойствам логарифма
.
По свойствам логарифма ![]() .
Дифференцирование обеих частей равенства
приводит к результату:
.
Дифференцирование обеих частей равенства
приводит к результату:

Ответ: ![]() .
.
Этот
же пример можно решить и без использования
логарифмической производной. Можно
провести некоторые преобразования и
перейти от дифференцирования показательно
степенной функции к нахождению производной
сложной функции:

Пример.
Найти
производную функции  .
.
Решение.
В
этом примере функция  представляет
собой дробь и ее производную можно
искать с использованием правил
дифференцирования. Но в силу громоздкости
выражения это потребует множества
преобразований. В таких случаях разумнее
использовать формулу логарифмической
производной
представляет
собой дробь и ее производную можно
искать с использованием правил
дифференцирования. Но в силу громоздкости
выражения это потребует множества
преобразований. В таких случаях разумнее
использовать формулу логарифмической
производной ![]() .
Почему? Вы сейчас поймете.
.
Почему? Вы сейчас поймете.
Найдем
сначала ![]() .
В преобразованиях будем использовать
свойства логарифма (логарифм дроби
равен разности логарифмов, а логарифм
произведения равен сумме логарифмов,
и еще степень у выражения под знаком
логарифма можно вынести как коэффициент
перед логарифмом):
.
В преобразованиях будем использовать
свойства логарифма (логарифм дроби
равен разности логарифмов, а логарифм
произведения равен сумме логарифмов,
и еще степень у выражения под знаком
логарифма можно вынести как коэффициент
перед логарифмом):
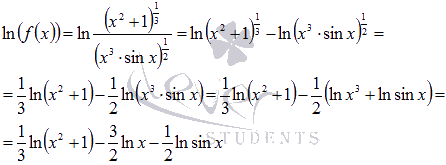
Эти
преобразования привели нас к достаточно
простому выражению, производная которого
легко находится:
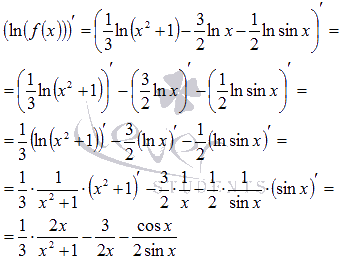
Подставляем
полученный результат в формулу
логарифмической производной и получаем
ответ:
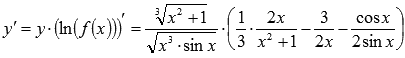
33.
Производные и дифференциалы высших
порядков. Применение.
Пусть
функция ![]() зависит
от переменной
зависит
от переменной ![]() и
дифференцируема в точке
и
дифференцируема в точке ![]() .
Может оказаться, что в точке
.
Может оказаться, что в точке ![]() дифференциал
дифференциал ![]() ,
рассматриваемый как функция от
,
рассматриваемый как функция от ![]() ,
есть также дифференцируемая функция.
Тогда существует дифференциал от
дифференциала
,
есть также дифференцируемая функция.
Тогда существует дифференциал от
дифференциала ![]() данной
функции, который называется дифференциалом
второго порядка функции
данной
функции, который называется дифференциалом
второго порядка функции ![]() .
Дифференциал второго порядка обозначается
следующим образом:
.
Дифференциал второго порядка обозначается
следующим образом:
![]()
Аналогично определяются дифференциалы более высоких порядков.
Определение
Дифференциалом ![]() -го
порядка
-го
порядка ![]() функции
функции ![]() называется
дифференциал от дифференциала
называется
дифференциал от дифференциала![]() -го
порядка этой функции, то есть
-го
порядка этой функции, то есть
![]()
Получим формулы, выражающие дифференциалы высших порядков. Рассмотрим несколько случаев.
Случай независимой переменной
Пусть ![]() -
функция независимой переменной
-
функция независимой переменной ![]() ,
имеющая дифференциалы любого порядка.
Первый дифференциал функции
,
имеющая дифференциалы любого порядка.
Первый дифференциал функции
![]()
где ![]() -
некоторое приращение независимой
переменной
-
некоторое приращение независимой
переменной ![]() ,
которое мы задаем сами и которое не
зависит от
,
которое мы задаем сами и которое не
зависит от ![]() .
По определению
.
По определению
![]()
Переменной
является аргумент ![]() .
Значит, для дифференциала величина
.
Значит, для дифференциала величина ![]() является
постоянной и поэтому может быть вынесена
за знак дифференциала. То есть дифференциал
второго порядка
является
постоянной и поэтому может быть вынесена
за знак дифференциала. То есть дифференциал
второго порядка
![]()
Для
вычисления дифференциала ![]() применим
формулу дифференциала первого порядка
к функции
применим
формулу дифференциала первого порядка
к функции ![]() .
Тогда получим:
.
Тогда получим:
![]()
Итак,
![]()
Рассматривая
последовательно дифференциалы все
более высокого порядка, получим формулу
дифференциала ![]() -го
порядка:
-го
порядка:
![]()
Пример
Задание. Найти
дифференциал третьего порядка функции ![]()
Решение. По формуле
![]()
Найдем третью производную заданной функции:
![]()
![]()
![]()
![]()
![]()
Тогда
![]()
Ответ. ![]()
Больше примеров решенийРешение производных онлайн
